吴恩达深度学习第二课第三周 超参数调试、Batch正则化和程序框架

1.调试处理
关于训练深度最难的事情之一是你要处理的参数的数量,从学习速率alpha到Momentum(动量梯度下降法)的参数theta。
如果使用Momentum或Adam优化算法的参数theta1,theta和Epsilon,也许你还得选择层数,也许你还得选择不同层中隐藏单元的数量,也许你还想使用学习率衰减。
所以,你使用的不是单一的学习率alpha,当然你可能还需要选择mini-batch的大小。
结果证实一些超参数比其它的更为重要,学习速率就是需要调试的最重要的超参数。

我们在进行超参调整的时候,在几个几何范围内进行尝试,如果找到一个较好的范围,则在这个范围继续细分尝试
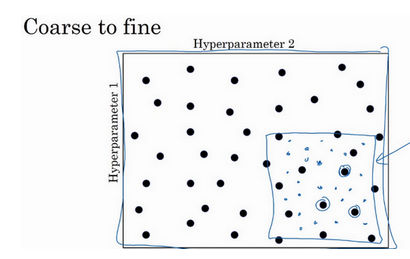
2. 超参数选择合适的范围
这一节讲怎样选择合适的标尺来寻找最优超参
假如我们设定学习率应该在0.001~1这个区间内比较好,我们怎么选择我们尝试的点呢?是1-0.001再除10?这样对于0.001~0.01这个区间我们使用了过少的资源,因此我们采用一种新的方式
我们使用0.001,0.01,0.1,1这几个 梯度来进行计算,这样在每一个梯度之间使用的资源几乎相等。
也就是我们在10的n次方上取等份。

3.归一化网络的激活函数
batch归一化会使你的参数搜索问题变得更加容易,使神经网络对超参的选择更加稳定,超参的范围会更加庞大,工作效果会更好,因此你训练起来也更容易。
之前我们学过输入数据的归一化,这次我们将输入的归一化引入到神经网络中,我们对w和b进行归一化,以达到一个比较好的效果
4.将Batch Norm拟合进神经网络
Batch归一化是发生在计算z和a之间。
实际上就是在每一次计算完z之后进行一次数据标准化(减去均值除以方差),然后在进行下一层计算,至于使用什么来激活,使用什么方法进行下降,都和这个没有关系
在框架中实际上只有一行代码就可以完成这个操作,比如在TensorFlow中,我们只需要tf.nn.batch_normalization即可完成batch Norm操作
我们一般将batch Norm与mini-batch组合使用。
5.Batch Norm为什么奏效
第一个原因,经过标准化的输入似的其均值为0,方差为1,因此我们可以将一个很大范围的输入值转换到0~1之间,可以加速学习。
另一个原因是它可以使权重比你的网络更滞后或更深层。
比如我们使用一个神经网络来训练猫的识别,我们所有的例子都是黑猫
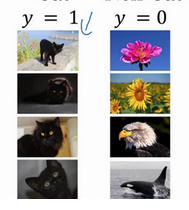
这时候如果我们测试其他颜色的猫
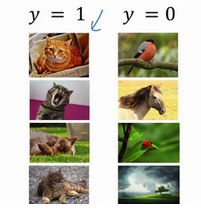
效果很可能不好,为了防止这种情况,我们需要使网络不过分依赖输入数据,这时候我们就可以引入Batch Norm,
我们可以把每一层神经网络拆开来,当前层的前一层为当前层的输入层,那么怎么使当前层不过分依赖前一层的值呢,就是标准化, 在前一层值的基础上重新计算一个方差为1平均值为0的一组数,让每一层网络都可以“独立”学习,以达到更好的效果。
当然,dropout也有一定的效果,有时候我们将dropout和batch norm合起来使用。
6.测试时的Batch Norm
我们在训练时由于使用了Batch Norm,每一层都进行标准化,但是我们在测试的时候,一个数据的标准化是没有意义的,因此我们需要估计这两个标准化的参数。
我们采用指数加权平均的方法来估计这两个数,根据训练过程中每个mini-batch的数求出平均值,用于测试。
实际上采用何种方法比如直接取最后一次是没有很大的影响的(但是实际上运用加权平均比较多),只要合理的取出这两个数值在测试中都会有效。
7.Softmax回归
对于多分类的问题,我们不能像之前二分类一样输出是不是的概率。
因此引入softmax,实际上就是输出层的激活函数,先对输出层取指数,然后求出一个和为1的概率值。
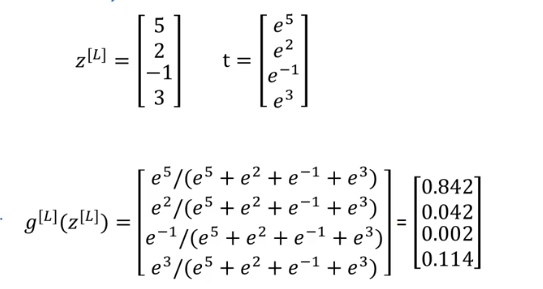
测验
1. 如果在大量的超参数中搜索最佳的参数值,那么应该尝试在网格中搜索而不是使用随机值,以便更系统的搜索,而不是依靠运气,请问这句话是正确的吗?
错误, 应当尝试随机值,不要使用网格搜索,因为你不知道哪些超参数比其他的更重要。
2. 每个超参数如果设置得不好,都会对训练产生巨大的负面影响,因此所有的超参数都要调整好,请问这是正确的吗?
错误,比如epsilon,就属于比较无关紧要的参数。
3. 在超参数搜索过程中,你尝试只照顾一个模型(使用熊猫策略)还是一起训练大量的模型(鱼子酱策略)在很大程度上取决于
- 是否使用批量(batch)或小批量优化(mini-batch optimization)
- 神经网络中局部最小值(鞍点)的存在性
- 在你能力范围内,你能够拥有多大的计算能力
- 需要调整的超参数的数量
3
4. 如果您认为β(动量超参数)介于0.9和0.99之间,那么推荐采用以下哪一种方法来对β值进行取样?
r = np.random.rand()
beta = 1 - 10 ** ( - r - 1 )5. 找到好的超参数的值是非常耗时的,所以通常情况下你应该在项目开始时做一次,并尝试找到非常好的超参数,这样你就不必再次重新调整它们。请问这正确吗?
错误, 模型中的细微变化可能导致您需要从头开始重新找到好的超参数。
6. 在视频中介绍的批量标准化中,如果将其应用于神经网络的第l层,那么您使用什么进行标准化?
z[l]
7.在标准化公式中,为什么要使用epsilon(ϵ)?
为了避免除0操作。
8. 批处理规范中关于 γ 和 β 的以下哪些陈述是正确的?
- 它们可以在Adam、具有动量的梯度下降或RMSprop使中用,而不仅仅是用梯度下降来学习。
- 它们设定给定层的线性变量 z[l] 的均值和方差。
1,2
9. 在训练具有批处理规范的神经网络之后,在测试时间,在新样本上评估神经网络,您应该:
执行所需的标准化,在训练期间使用使用了μ和σ2的指数加权平均值来估计mini-batches的情况。
10. 关于深度学习编程框架的这些陈述中,哪一个是正确的?
- 通过编程框架,您可以使用比低级语言(如Python)更少的代码来编写深度学习算法。
- 即使一个项目目前是开源的,项目的良好管理有助于确保它即使在长期内仍然保持开放,而不是仅仅为了一个公司而关闭或修改。
- 深度学习编程框架的运行需要基于云的机器。
1,2
编程作业
首先进行TensorFlow入门:
导包:
import tensorflow as tf
定义损失:
# 计算损失
# 定义y_hat为36
y_hat = tf.constant(36, name='y_hat')
# 定义y为39
y = tf.constant(39, name='y')
# 定义损失函数
loss = tf.Variable((y - y_hat) ** 2, name='loss')
# 初始化参数
init = tf.global_variables_initializer()
with tf.Session() as session:
session.run(init)
print(session.run(loss))
程序输出为9。
placeholder占位符
# 使用placeholder占位符
x = tf.placeholder(tf.int64, name="x")
with tf.Session() as session:
print(session.run(2 * x, feed_dict={x: 3}))
程序输出为6。
下面是计算线性函数:
# 计算线性函数
def linear_function():
"""
实现一个计算线性函数的功能
:return:
"""
X = np.random.randn(3, 1)
W = np.random.randn(4, 3)
b = np.random.randn(4, 1)
Y = tf.add(tf.matmul(W, X), b)
# 这俩是一样的,因为如果tf会重载运算符
Y = tf.matmul(W, X) + b
with tf.Session() as session:
result = session.run(Y)
session.close()
return result
print("result = " + str(linear_function()))
输出:
result = [[-2.15657382] [ 2.95891446] [-1.08926781] [-0.84538042]]
sigmoid:
# sigmoid
def sigmoid(z):
"""
sigmoid
:param z:
:return:
"""
x = tf.placeholder(tf.float32, name='x')
sigmoid = tf.sigmoid(x)
with tf.Session() as session:
result = session.run(sigmoid, feed_dict={x: z})
return result
print("sigmoid(0) = " + str(sigmoid(0)))
print("sigmoid(12) = " + str(sigmoid(12)))
输出:
# sigmoid(0) = 0.5 # sigmoid(12) = 0.9999938
one-hot矩阵,就是将结果向量转化为矩阵的形式:
# one-hot矩阵
def one_hot_matrix(labels, C):
"""
生成onehot矩阵
:param labels:标签向量
:param C:分类数
:return:
"""
C = tf.constant(C, name='C')
one_hot_matrix = tf.one_hot(indices=labels, depth=C, axis=0)
with tf.Session() as session:
result = session.run(one_hot_matrix)
session.close()
return result
labels = np.array([1, 2, 3, 0, 2, 1])
one_hot = one_hot_matrix(labels, C=4)
print(str(one_hot))
输出:
[[0. 0. 0. 1. 0. 0.]
[1. 0. 0. 0. 0. 1.]
[0. 1. 0. 0. 1. 0.]
[0. 0. 1. 0. 0. 0.]]
下面就是使用TensorFlow来写一个识别手势的神经网络,首先导包:
import numpy as np import matplotlib.pyplot as plt import tensorflow as tf from course_2_week_3 import tf_utils import time
首先加载数据,并随机打印一个看看:
# 加载数据
X_train_orig, Y_train_orig, X_test_orig, Y_test_orig, classes = tf_utils.load_dataset()
plt.imshow(X_train_orig[11])
print("Y = " + str(np.squeeze(Y_train_orig[:, 11])))
plt.show()
可以看到这个是1:
然后我们将训练数据转置、标准化并将结果集变成one-hot矩阵。
X_train_flatten = X_train_orig.reshape(X_train_orig.shape[0], -1).T
X_test_flatten = X_test_orig.reshape(X_test_orig.shape[0], -1).T
# 归一化数据
X_train = X_train_flatten / 255
X_test = X_test_flatten / 255
# 转换onehot矩阵
Y_train = tf_utils.convert_to_one_hot(Y_train_orig, 6)
Y_test = tf_utils.convert_to_one_hot(Y_test_orig, 6)
然后我们定义placeholder生成函数:
def create_placeholders(n_x, n_y):
"""
为TensorFlow会话创建占位符
:param n_x:
:param n_y:
:return:
"""
X = tf.placeholder(tf.float32, [n_x, None], name='X')
Y = tf.placeholder(tf.float32, [n_y, None], name='Y')
return X, Y
参数的初始化:
def initialize_parameters():
"""
初始化参数
:return:
"""
W1 = tf.get_variable('W1', [25, 12288], initializer=tf.contrib.layers.xavier_initializer(seed=1))
b1 = tf.get_variable('b1', [25, 1], initializer=tf.zeros_initializer())
W2 = tf.get_variable('W2', [12, 25], initializer=tf.contrib.layers.xavier_initializer(seed=1))
b2 = tf.get_variable('b2', [12, 1], initializer=tf.zeros_initializer())
W3 = tf.get_variable('W3', [6, 12], initializer=tf.contrib.layers.xavier_initializer(seed=1))
b3 = tf.get_variable('b3', [6, 1], initializer=tf.zeros_initializer())
return {
'W1': W1,
'b1': b1,
'W2': W2,
'b2': b2,
'W3': W3,
'b3': b3
}
前向传播:
def forward_propagation(X, parameters):
"""
前向传播
:param X:
:param parameters:
:return:
"""
W1 = parameters['W1']
b1 = parameters['b1']
W2 = parameters['W2']
b2 = parameters['b2']
W3 = parameters['W3']
b3 = parameters['b3']
Z1 = tf.matmul(W1, X) + b1
A1 = tf.nn.relu(Z1)
Z2 = tf.matmul(W2, A1) + b2
A2 = tf.nn.relu(Z2)
Z3 = tf.matmul(W3, A2) + b3
return Z3
计算代价:
def compute_cost(Z3, Y):
"""
计算代价
:param Z3:
:param Y:
:return:
"""
logits = tf.transpose(Z3)
labels = tf.transpose(Y)
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels=labels))
return cost
编写模型并对模型进行保存:
def model(X_train, Y_train, X_test, Y_test, learning_rate=0.0001, num_epochs=1300, minibatch_size=32,
print_cost=True,
is_plot=True):
"""
神经网络模型
LINEAR->RELU->LINEAR->RELU->LINEAR->SOFTMAX
:param X_train:
:param Y_train:
:param X_test:
:param Y_test:
:param learning_rate:
:param num_epochs:
:param minbatch_size:
:param print_cost:
:param is_plot:
:return:
"""
n_x, m = X_train.shape
n_y = Y_train.shape[0]
costs = []
# 创建placeholder
X, Y = create_placeholders(n_x, n_y)
# 初始化参数
parameters = initialize_parameters()
# 前行传播
Z3 = forward_propagation(X, parameters)
# 计算成本
cost = compute_cost(Z3, Y)
# 反向传播,Adam优化
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost)
saver = tf.train.Saver()
# 初始化所有的变量
init = tf.global_variables_initializer()
# 开始会话并计算
with tf.Session() as session:
session.run(init)
# 循环
for epoch in range(num_epochs):
epoch_cost = 0
num_minbatches = int(m / minibatch_size)
minibatches = tf_utils.random_mini_batches(X_train, Y_train, minibatch_size)
for minibatch in minibatches:
minibatch_X, minibatch_Y = minibatch
# 开始运行
_, minibatch_cost = session.run([optimizer, cost], feed_dict={X: minibatch_X, Y: minibatch_Y})
# 计算代价
epoch_cost = epoch_cost + minibatch_cost / num_minbatches
# 记录代价
if epoch % 5 == 0:
costs.append(epoch_cost)
if print_cost and epoch % 100 == 0:
print("epoch = " + str(epoch) + " epoch_cost = " + str(epoch_cost))
saver.save(session, './model/my_model', global_step=100)
# 是否绘制图谱
if is_plot:
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
# 保存参数
parameters = session.run(parameters)
# 计算预测结果
current_prediction = tf.equal(tf.argmax(Z3), tf.argmax(Y))
# 计算准确率
accuracy = tf.reduce_mean(tf.cast(current_prediction, 'float'))
print("训练集的准确率:", accuracy.eval({X: X_train, Y: Y_train}))
print("测试集的准确率:", accuracy.eval({X: X_test, Y: Y_test}))
return parameters
调用网络:
# 开始时间
start_time = time.clock()
# 开始训练
parameters = model(X_train, Y_train, X_test, Y_test)
# 结束时间
end_time = time.clock()
# 计算时差
print("CPU的执行时间 = " + str(end_time - start_time) + " 秒")
我们可以看到训练结果(过程较慢):
epoch = 0 epoch_cost = 1.8670177423592766
epoch = 100 epoch_cost = 1.0305518833073701
epoch = 200 epoch_cost = 0.7247187675851763
epoch = 300 epoch_cost = 0.49531238006822986
epoch = 400 epoch_cost = 0.33661927914980694
epoch = 500 epoch_cost = 0.2284338934855028
epoch = 600 epoch_cost = 0.17487916463252268
epoch = 700 epoch_cost = 0.11813201111826033
epoch = 800 epoch_cost = 0.08827614908417065
epoch = 900 epoch_cost = 0.06095291397562531
epoch = 1000 epoch_cost = 0.04344996804315032
epoch = 1100 epoch_cost = 0.11286204381648339
epoch = 1200 epoch_cost = 0.04022079737236102
epoch = 1300 epoch_cost = 0.03377958937463435
epoch = 1400 epoch_cost = 0.07520042944022201
训练集的准确率: 0.9962963
测试集的准确率: 0.825
CPU的执行时间 = 433.66559440000003 秒
图片,可以看到由于mini-batch造成的起伏。
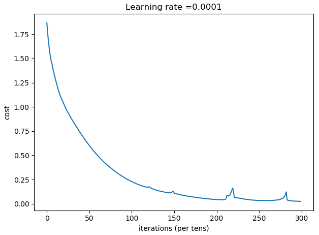
完整代码:
# -*- coding:utf-8 -*-
"""
┏┛ ┻━━━━━┛ ┻┓
┃ ┃
┃ ━ ┃
┃ ┳┛ ┗┳ ┃
┃ ┃
┃ ┻ ┃
┃ ┃
┗━┓ ┏━━━┛
┃ ┃ 神兽保佑
┃ ┃ 代码无BUG!
┃ ┗━━━━━━━━━┓
┃ ┣┓
┃ ┏┛
┗━┓ ┓ ┏━━━┳ ┓ ┏━┛
┃ ┫ ┫ ┃ ┫ ┫
┗━┻━┛ ┗━┻━┛
"""
import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from course_2_week_3 import tf_utils
import time
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
# 加载数据
X_train_orig, Y_train_orig, X_test_orig, Y_test_orig, classes = tf_utils.load_dataset()
# plt.imshow(X_train_orig[11])
# print("Y = " + str(np.squeeze(Y_train_orig[:, 11])))
# plt.show()
X_train_flatten = X_train_orig.reshape(X_train_orig.shape[0], -1).T
X_test_flatten = X_test_orig.reshape(X_test_orig.shape[0], -1).T
# 归一化数据
X_train = X_train_flatten / 255
X_test = X_test_flatten / 255
# 转换onehot矩阵
Y_train = tf_utils.convert_to_one_hot(Y_train_orig, 6)
Y_test = tf_utils.convert_to_one_hot(Y_test_orig, 6)
def create_placeholders(n_x, n_y):
"""
为TensorFlow会话创建占位符
:param n_x:
:param n_y:
:return:
"""
X = tf.placeholder(tf.float32, [n_x, None], name='X')
Y = tf.placeholder(tf.float32, [n_y, None], name='Y')
return X, Y
# 初始化参数
def initialize_parameters():
"""
初始化参数
:return:
"""
W1 = tf.get_variable('W1', [25, 12288], initializer=tf.contrib.layers.xavier_initializer(seed=1))
b1 = tf.get_variable('b1', [25, 1], initializer=tf.zeros_initializer())
W2 = tf.get_variable('W2', [12, 25], initializer=tf.contrib.layers.xavier_initializer(seed=1))
b2 = tf.get_variable('b2', [12, 1], initializer=tf.zeros_initializer())
W3 = tf.get_variable('W3', [6, 12], initializer=tf.contrib.layers.xavier_initializer(seed=1))
b3 = tf.get_variable('b3', [6, 1], initializer=tf.zeros_initializer())
return {
'W1': W1,
'b1': b1,
'W2': W2,
'b2': b2,
'W3': W3,
'b3': b3
}
def forward_propagation(X, parameters):
"""
前向传播
:param X:
:param parameters:
:return:
"""
W1 = parameters['W1']
b1 = parameters['b1']
W2 = parameters['W2']
b2 = parameters['b2']
W3 = parameters['W3']
b3 = parameters['b3']
Z1 = tf.matmul(W1, X) + b1
A1 = tf.nn.relu(Z1)
Z2 = tf.matmul(W2, A1) + b2
A2 = tf.nn.relu(Z2)
Z3 = tf.matmul(W3, A2) + b3
return Z3
def compute_cost(Z3, Y):
"""
计算代价
:param Z3:
:param Y:
:return:
"""
logits = tf.transpose(Z3)
labels = tf.transpose(Y)
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels=labels))
return cost
def model(X_train, Y_train, X_test, Y_test, learning_rate=0.0001, num_epochs=1300, minibatch_size=32,
print_cost=True,
is_plot=True):
"""
神经网络模型
LINEAR->RELU->LINEAR->RELU->LINEAR->SOFTMAX
:param X_train:
:param Y_train:
:param X_test:
:param Y_test:
:param learning_rate:
:param num_epochs:
:param minbatch_size:
:param print_cost:
:param is_plot:
:return:
"""
n_x, m = X_train.shape
n_y = Y_train.shape[0]
costs = []
# 创建placeholder
X, Y = create_placeholders(n_x, n_y)
# 初始化参数
parameters = initialize_parameters()
# 前行传播
Z3 = forward_propagation(X, parameters)
# 计算成本
cost = compute_cost(Z3, Y)
# 反向传播,Adam优化
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost)
saver = tf.train.Saver()
# 初始化所有的变量
init = tf.global_variables_initializer()
# 开始会话并计算
with tf.Session() as session:
session.run(init)
# 循环
for epoch in range(num_epochs):
epoch_cost = 0
num_minbatches = int(m / minibatch_size)
minibatches = tf_utils.random_mini_batches(X_train, Y_train, minibatch_size)
for minibatch in minibatches:
minibatch_X, minibatch_Y = minibatch
# 开始运行
_, minibatch_cost = session.run([optimizer, cost], feed_dict={X: minibatch_X, Y: minibatch_Y})
# 计算代价
epoch_cost = epoch_cost + minibatch_cost / num_minbatches
# 记录代价
if epoch % 5 == 0:
costs.append(epoch_cost)
if print_cost and epoch % 100 == 0:
print("epoch = " + str(epoch) + " epoch_cost = " + str(epoch_cost))
saver.save(session, './model/my_model', global_step=100)
# 是否绘制图谱
if is_plot:
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
# 保存参数
parameters = session.run(parameters)
# 计算预测结果
current_prediction = tf.equal(tf.argmax(Z3), tf.argmax(Y))
# 计算准确率
accuracy = tf.reduce_mean(tf.cast(current_prediction, 'float'))
print("训练集的准确率:", accuracy.eval({X: X_train, Y: Y_train}))
print("测试集的准确率:", accuracy.eval({X: X_test, Y: Y_test}))
return parameters
# 开始时间
start_time = time.cl ock()
# 开始训练
parameters = model(X_train, Y_train, X_test, Y_test)
# 结束时间
end_time = time.clock()
# 计算时差
print("CPU的执行时间 = " + str(end_time - start_time) + " 秒")
"""
epoch = 0 epoch_cost = 1.8670177423592766
epoch = 100 epoch_cost = 1.0305518833073701
epoch = 200 epoch_cost = 0.7247187675851763
epoch = 300 epoch_cost = 0.49531238006822986
epoch = 400 epoch_cost = 0.33661927914980694
epoch = 500 epoch_cost = 0.2284338934855028
epoch = 600 epoch_cost = 0.17487916463252268
epoch = 700 epoch_cost = 0.11813201111826033
epoch = 800 epoch_cost = 0.08827614908417065
epoch = 900 epoch_cost = 0.06095291397562531
epoch = 1000 epoch_cost = 0.04344996804315032
epoch = 1100 epoch_cost = 0.11286204381648339
epoch = 1200 epoch_cost = 0.04022079737236102
epoch = 1300 epoch_cost = 0.03377958937463435
epoch = 1400 epoch_cost = 0.07520042944022201
训练集的准确率: 0.9962963
测试集的准确率: 0.825
CPU的执行时间 = 433.66559440000003 秒
"""
0 条评论