【深度学习笔记】对抗训练

当说到对抗训练时，我们一般想到的是对抗生成网络（GAN）和对抗攻击、对抗样本等。

这里我们主要讲对抗攻击、对抗样本。它主要关心模型在小扰动下的稳健性。

比如，在cv领域，我们可以通过在原图像中加入噪点，但是并不影响原图像的性质。

而在NLP领域，我们并不能直接的通过在词编码上添加噪点，因为词嵌入本质上就是one-hot，如果在one-hot上增加上述噪点，就会对原句产生歧义。

因此，一个自然的想法就是在embedding上增加扰动，但有个问题是扰动后的embedding不一定能匹配到原来的emebdding（也就是语义可能会发生变化），这样样本就发生了变化。

但是这个思路依然会有一定的提升。

我们可以简单地直接对embedding参数矩阵进行扰动来获得样本的多样性。

keras代码如下：

def adversarial_training(model, embedding_name, epsilon=1):
    """给模型添加对抗训练
    其中model是需要添加对抗训练的keras模型，embedding_name
    则是model里边Embedding层的名字。要在模型compile之后使用。
    """
    if model.train_function is None:  # 如果还没有训练函数
        model._make_train_function()  # 手动make
    old_train_function = model.train_function  # 备份旧的训练函数
    # 查找Embedding层
    for output in model.outputs:
        embedding_layer = search_layer(output, embedding_name)
        if embedding_layer is not None:
            break
    if embedding_layer is None:
        raise Exception('Embedding layer not found')
    # 求Embedding梯度
    embeddings = embedding_layer.embeddings  # Embedding矩阵
    gradients = K.gradients(model.total_loss, [embeddings])  # Embedding梯度
    gradients = K.zeros_like(embeddings) + gradients[0]  # 转为dense tensor
    # 封装为函数
    inputs = (model._feed_inputs +
              model._feed_targets +
              model._feed_sample_weights)  # 所有输入层
    embedding_gradients = K.function(
        inputs=inputs,
        outputs=[gradients],
        name='embedding_gradients',
    )  # 封装为函数
    def train_function(inputs):  # 重新定义训练函数
        grads = embedding_gradients(inputs)[0]  # Embedding梯度
        delta = epsilon * grads / (np.sqrt((grads**2).sum()) + 1e-8)  # 计算扰动
        K.set_value(embeddings, K.eval(embeddings) + delta)  # 注入扰动
        outputs = old_train_function(inputs)  # 梯度下降
        K.set_value(embeddings, K.eval(embeddings) - delta)  # 删除扰动
        return outputs
    model.train_function = train_function  # 覆盖原训练函数

然后我们只需要：

# 写好函数后，启用对抗训练只需要一行代码
adversarial_training(model, 'Embedding-Token', 0.5)

即可添加这个扰动。

不过需要注意的是，由于在添加扰动的时候计算了一次梯度，因此embedding实际上的时间增加了一倍。

流程图如下：

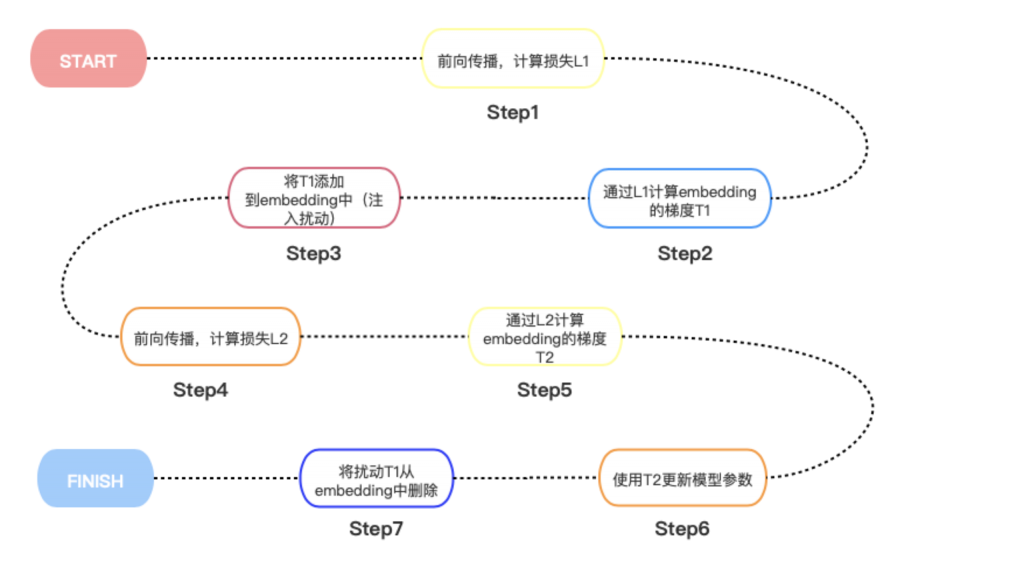
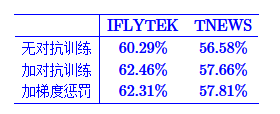
实际效果在CLUE的两个分类任务上有一定的效果

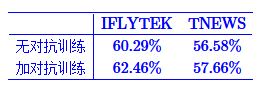
另一个有趣的对抗方法是梯度惩罚。

简单来说就是向loss中添加一个“梯度惩罚”。

图形理解就是：

假设我们的任务有n个分类，那么我们的模型相当于挖了n个坑。

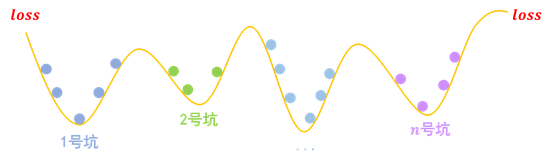
而梯度惩罚，则要求“同类样本不仅要放在同一个坑内，还要放在坑底”。这就要求每个坑内长这样：

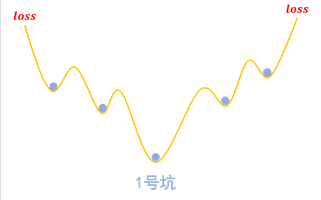
由于不容易发生干扰（坑底稳定），因此也就达到了对抗训练的目的。

代码：

def sparse_categorical_crossentropy(y_true, y_pred):
    """自定义稀疏交叉熵
    这主要是因为keras自带的sparse_categorical_crossentropy不支持求二阶梯度。
    """
    y_true = K.reshape(y_true, K.shape(y_pred)[:-1])
    y_true = K.cast(y_true, 'int32')
    y_true = K.one_hot(y_true, K.shape(y_pred)[-1])
    return K.categorical_crossentropy(y_true, y_pred)
def loss_with_gradient_penalty(y_true, y_pred, epsilon=1):
    """带梯度惩罚的loss
    """
    loss = K.mean(sparse_categorical_crossentropy(y_true, y_pred))
    embeddings = search_layer(y_pred, 'Embedding-Token').embeddings
    gp = K.sum(K.gradients(loss, [embeddings])[0].values**2)
    return loss + 0.5 * epsilon * gp
model.compile(
    loss=loss_with_gradient_penalty,
    optimizer=Adam(2e-5),
    metrics=['sparse_categorical_accuracy'],
)

效果依然不错：