【LeetCode】*0085 最大矩形

https://leetcode-cn.com/problems/maximal-rectangle/

# -*- coding:utf-8 -*-

class Solution(object):
    def maximalRectangle(self, matrix):
        """
        :type matrix: List[List[str]]
        :rtype: int
        """
        if not matrix: return 0
        m = len(matrix)
        n = len(matrix[0])
        left = [0] * n  # initialize left as the leftmost boundary possible
        right = [n] * n  # initialize right as the rightmost boundary possible
        height = [0] * n
        maxarea = 0
        for i in range(m):
            cur_left, cur_right = 0, n
            # update height
            for j in range(n):
                if matrix[i][j] == '1':
                    height[j] += 1
                else:
                    height[j] = 0
            # update left
            for j in range(n):
                if matrix[i][j] == '1':
                    left[j] = max(left[j], cur_left)
                else:
                    left[j] = 0
                    cur_left = j + 1
            # update right
            for j in range(n - 1, -1, -1):
                if matrix[i][j] == '1':
                    right[j] = min(right[j], cur_right)
                else:
                    right[j] = n
                    cur_right = j
            # update the area
            for j in range(n):
                maxarea = max(maxarea, height[j] * (right[j] - left[j]))
        return maxarea
if __name__ == '__main__':
    matrix = [
        ["1", "0", "0", "0", "0"],
        ["1", "0", "1", "1", "1"],
        ["1", "1", "1", "1", "1"],
        ["1", "0", "0", "1", "0"]
    ]
    print(Solution().maximalRectangle(matrix))

思路：这道题一看就感觉是动态规划，但是动态规划其实难就难在找状态，这道题我思考了很久尝试找出状态，刚开始想的就是max area，后来发现不行，要带边状态，然后又尝试m*n,area的组合，但是依然不行。

最后看题解发现这道题有两种dp思路，一种是较差的。

对每一行连续的1进行判断，然后在判断最大矩形，也就是在长宽相同的矩阵中复杂度达到了n3。

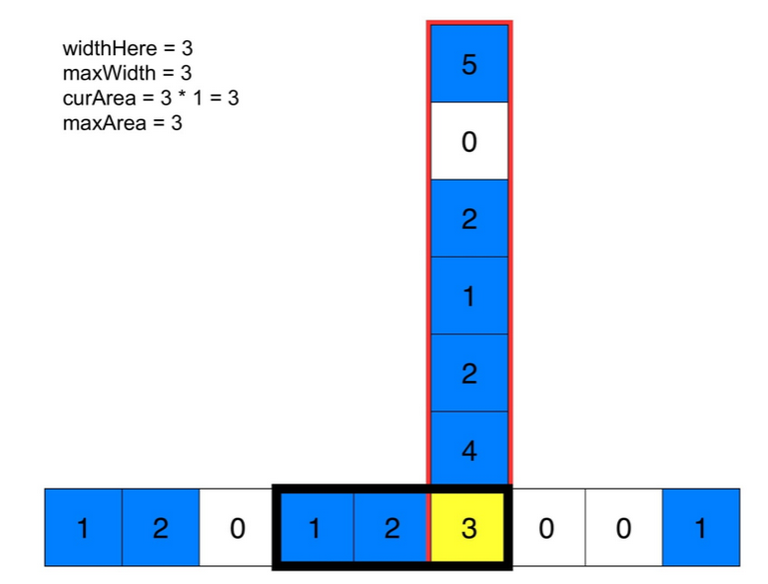
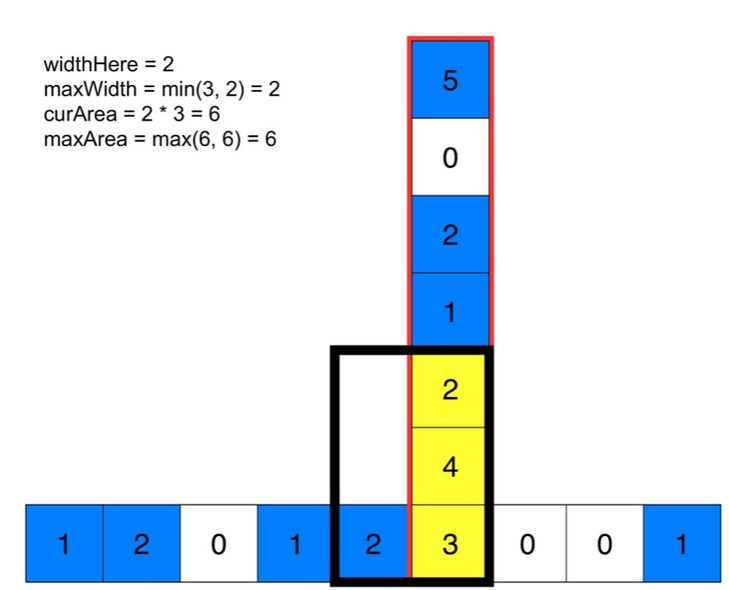
第二种较好的思想复杂度在矩阵中达到了n2。

找左边第一个非1位置和右边第一个非1位置，那么最大的区域就可以被左右两个夹出来，在添加一个高度列表，就可以算出最大矩阵。

如下图，我们虚拟出来一个第五列，假如我们算在第2行，因此有height、left、right如右边所示：

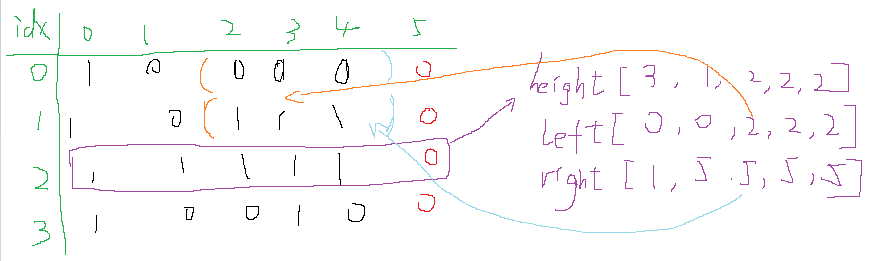
对于height，就是连续多少个1，对于left是当前列在之前出现过的行中最大的1索引，也就是尽可能靠右，然后right同理，这时候我们就在这行可以求出最大矩形面积( right-left )*height = （ 5-2 ）*2