【吴恩达深度学习】浅层神经网络

吴恩达深度学习第一课第三周，浅层神经网络

1.什么是神经网络

神经网络其实就是多个逻辑回归单元的堆叠。

比如下图：

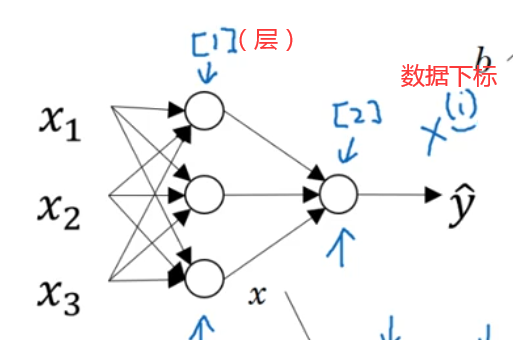
这张图片实际上就是4个逻辑回归单元的堆叠，对于【2】层，是由【1】层的数据作逻辑回归得到【2】层数据，而【1】层数据又是分别由输入层x做了三次逻辑回归得到的输出。

对于这些层的叫法，我们还有其他叫法：

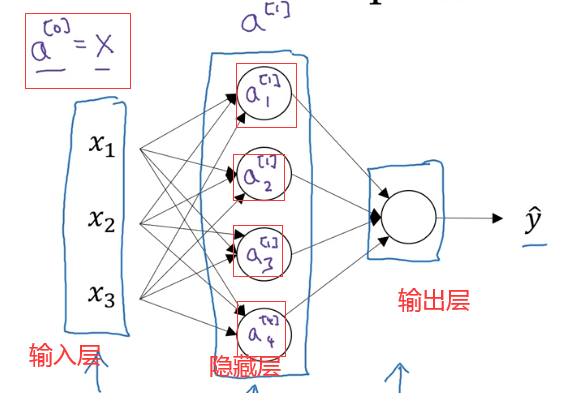
分别为输入层，隐藏层（可以大于一层）和输出层组成，其中的结点表示也在图中有标识。

2.神经元里有什么？

既然本质上和逻辑回归差不多，那么神经元的实际运算也和逻辑回归大同小异。

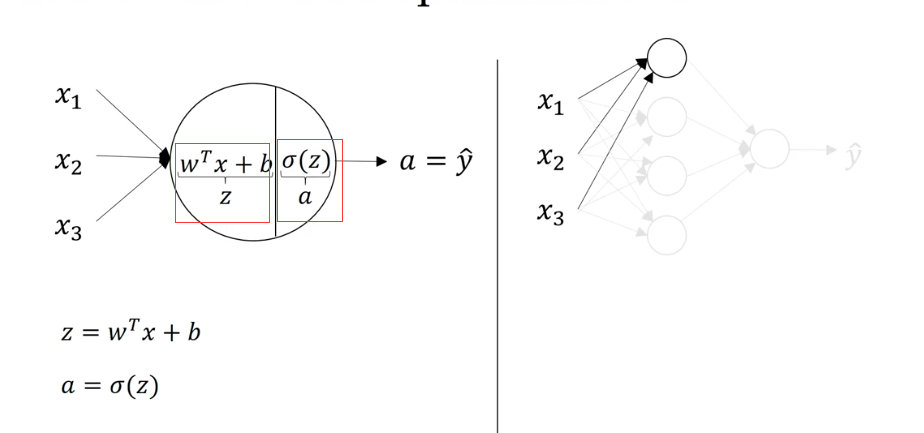
实际上就是z = wx + b和一个激活过程，和上一周讲的基于逻辑回归的神经网络是一样的，和基础逻辑回归也就多了一个偏置b。

因此对于整个神经网络，我们可以获得如下式子：

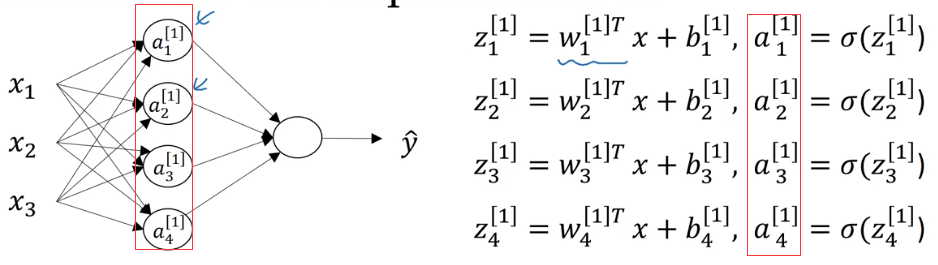
为了计算方便，我们向量化表示这些计算过程（这里是一次计算三个样本的情况）

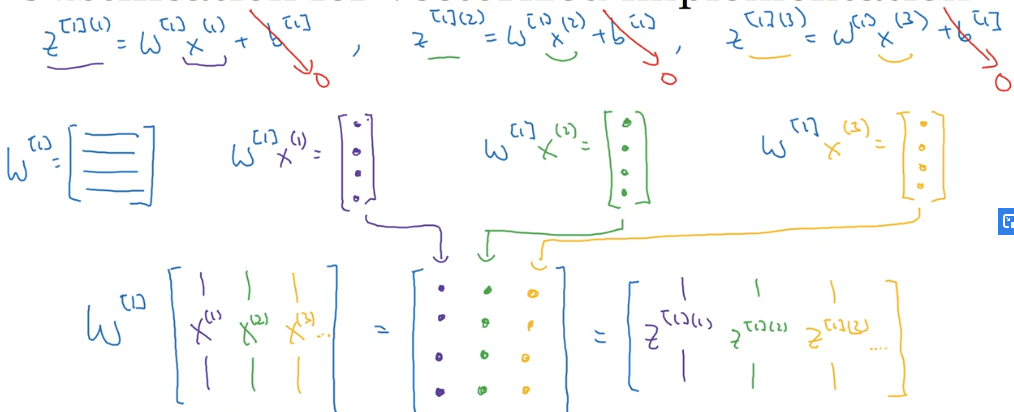
3.激活函数

我们有三（四）种激活函数，分别为：

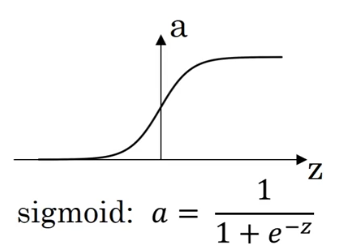
sigmoid激活函数

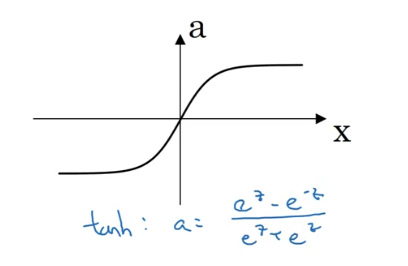
tanh激活函数

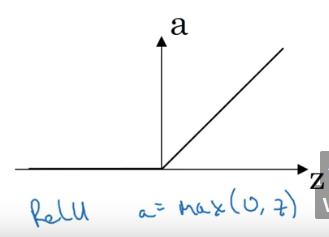
ReLU激活函数

和ReLU的变种，带泄漏的ReLU激活函数（注意到在x负半轴不再是一条水平直线，而是又一个微小斜率的曲线）

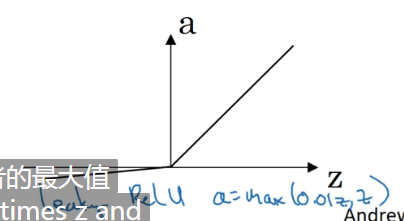
对于这么多种激活函数，怎么使用和区分呢？

对于sigmoid激活函数，是一个很古老的激活函数，它和其他激活函数一样，都将很大范围的x值映射到一个很小的范围之内。

对于tanh激活函数，它的表现往往优于sigmoid激活函数，因此多使用tanh。但是也不是绝对的，有一个特例就是二分类问题，因为我们最后的输出概率在0~1之间会更加合理，因此输出层的激活函数往往使用的是sigmoid激活函数。即使这样，在这之前的隐藏层，依然推荐使用tanh激活函数或者ReLU激活函数。

但是sigmoid激活函数和tanh激活函数都有一个问题，就是当x足够大或者足够小的时候，激活函数的斜率趋近于0，这样会导致整体的学习速率下降，减慢学习的速度，因此我们引入了另一个激活函数。

ReLU激活函数（a = max(0,z)）,只要z为复述，斜率为0，z为正数斜率为1。对于这个激活函数，只有几句话来描述，好用，用就完事了，不知道用啥就用它，指定没错。

还有一个就是带泄漏的ReLU函数，这个函数在x负半轴有一个斜率很小的取消，通常取0.01，这只是个经验值，在一些情况下需要试验其他值。但是往往使用ReLU激活函数就可以了。

因此我们总结一下就是ReLU用就完事了，sigmoid除了二分类的输出层最好不用。

4.为什么要使用非线性的激活函数？

我们可以发现上面说的几个激活函数都是非（全局）线性的，那么为什么要使用非线性的激活函数呢？

事实证明，如果要让你的神经网络有一个比较好的输出，必须使用非线性的激活函数。

因为如果使用线性的激活函数，最后我们 可以化简发现，整个神经网络实际上还是在做线性在组合，实际上还是线性拟合，就从神经网络退化到了逻辑回归。

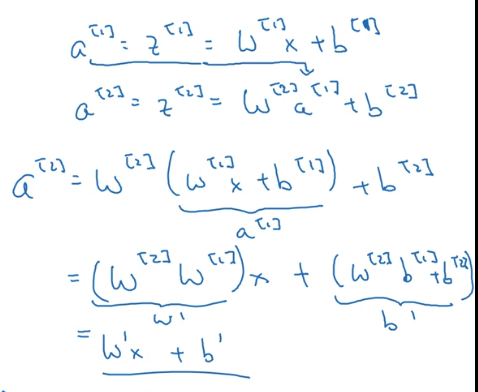
也就是说，不管多少层的神经网络，如果使用线性激活函数，那么和最简单的逻辑回归的结果是一样的。

5.随机初始化

对于参数w的选择，如果我们全部初始化为0

我们可以发现不管经过多少次计算，隐藏层的神经元的值都是一样的，因为它们有着同样的输入、同样的权重、同样的激活函数，因此必然有同样的结果。也就失去了多神经元的意义，我们称这种问题叫网络的对称性问题。

因此我们采用随机初始化w为一个很小的数，因为b没有对称性的问题，因此我们可以随意初始化，可以初始化为0。

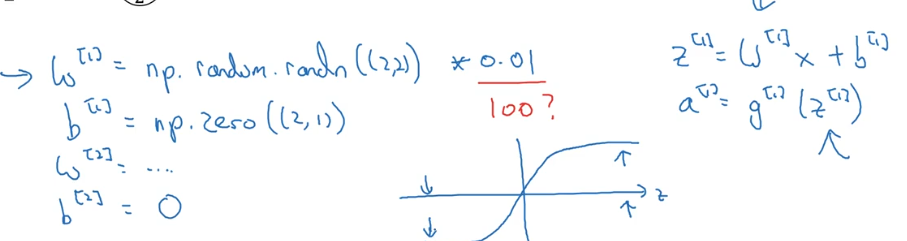
为什么随机初始化w为一个很小的数呢（也就是为什么乘0.01而不是100），因为z = wx + b，如果w比较大，z也就大，因此在激活的时候会激活到接近1的位置，斜率比较低，学习速度比较慢（当然ReLU并不存在这个问题）。

测验

1. 以下哪一项是正确的？

1. X是一个矩阵，其中每个列都是一个训练示例。
2. a[2]4 是第二层第四层神经元的激活的输出。
3. a[2](12)表示第二层和第十二层的激活向量。
4. a[2] 表示第二层的激活向量。

1，2，3，4。

2. tanh激活函数通常比隐藏层单元的sigmoid激活函数效果更好，因为其输出的平均值更接近于零，因此它将数据集中在下一层是更好的选择，请问正确吗？

正确

3. 其中哪一个是第l层向前传播的正确向量化实现，其中1≤l≤L

答案：

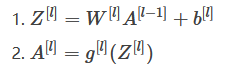
4. 您正在构建一个识别黄瓜（y = 1）与西瓜（y = 0）的二元分类器。 你会推荐哪一种激活函数用于输出层？

1. ReLU
2. Leaky ReLU
3. sigmoid
4. tanh

3， 来自sigmoid函数的输出值可以很容易地理解为概率。

5. 看一下下面的代码， 请问B.shape的值是多少?

A = np.random.randn(4,3)
B = np.sum(A, axis = 1, keepdims = True)

（4，1）由于keepdims=True的存在，会保持矩阵的性质而不会变成（4，）的数组形式。

6. 假设你已经建立了一个神经网络。 您决定将权重和偏差初始化为零。 以下哪项陈述是正确的？

1. 第一个隐藏层中的每个神经元节点将执行相同的计算。 所以即使经过多次梯度下降迭代后，层中的每个神经元节点都会计算出与其他神经元节点相同的东西。
2. 第一个隐藏层中的每个神经元将在第一次迭代中执行相同的计算。 但经过一次梯度下降迭代后，他们将学会计算不同的东西，因为我们已经“破坏了对称性”。
3. 第一个隐藏层中的每一个神经元都会计算出相同的东西，但是不同层的神经元会计算不同的东西，因此我们已经完成了“对称破坏”。
4. 即使在第一次迭代中，第一个隐藏层的神经元也会执行不同的计算， 他们的参数将以自己的方式不断发展。

1.

7. Logistic回归的权重w应该随机初始化，而不是全零，因为如果初始化为全零，那么逻辑回归将无法学习到有用的决策边界，因为它将无法“破坏对称性”，是正确的吗？

错误。 Logistic回归没有隐藏层，因此不存在多个神经元有对称性导致隐藏层失效。

8. 您已经为所有隐藏单元使用tanh激活建立了一个网络。 使用np.random.randn（..，..）* 1000将权重初始化为相对较大的值。 会发生什么？

1. 这没关系。只要随机初始化权重，梯度下降不受权重大小的影响。
2. 这将导致tanh的输入也非常大，因此导致梯度也变大。因此，您必须将α设置得非常小以防止发散; 这会减慢学习速度。
3. 这会导致tanh的输入也非常大，导致单位被“高度激活”，从而加快了学习速度，而权重必须从小数值开始。
4. 这将导致tanh的输入也很大，因此导致梯度接近于零， 优化算法将因此变得缓慢。

4。 tanh对于较大的值变得平坦，这导致其梯度接近于零。 这减慢了优化算法。

9.观察下面的神经网络：

1. b[1] 的维度是(4, 1)
2. W[1] 的维度是 (4, 2)
3. W[2] 的维度是 (1, 4)
4. b[2] 的维度是 (1, 1)

1，2，3，4。

10. 上一个网络中，z[1] 和 A[1]的维度是多少（z = wx + b）？

z[1] （4，m），A[1]（4，m）。（m是样本个数）。

编程作业

首先导入相关的包

import numpy as np
import matplotlib.pyplot as plt
from course_1_week_3.testCases import *
import sklearn.linear_model
from course_1_week_3.planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset, load_extra_datasets

然后加载数据并查看：

# 加载数据
X, Y = load_planar_dataset()
print('X的维度:', X.shape)
print('Y的维度:', Y.shape)
plt.title('show point')
plt.scatter(X[0, :], X[1, :], c=Y[0, :], s=40, cmap=plt.cm.Spectral)
plt.show()

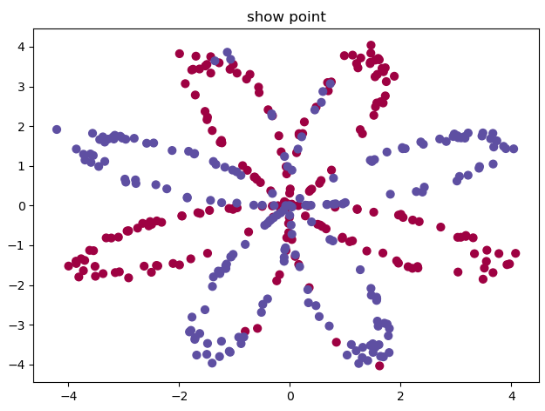
可以看到数据的样子。这时候我们尝试使用逻辑回归来进行分类。

# 使用逻辑回归处理
clf = sklearn.linear_model.LogisticRegression()
clf.fit(X.T, Y.T)
# planar_util里的方法   绘制决策边界
plot_decision_boundary(lambda x: clf.predict(x), X, Y[0, :])
plt.title('Logistic Regression')
LR_predictions = clf.predict(X.T)
print("逻辑回归的准确性： %d " % float((np.dot(Y, LR_predictions) +
                               np.dot(1 - Y, 1 - LR_predictions)) / float(Y.size) * 100) +
      "% " + "(正确标记的数据点所占的百分比)")
plt.show()

画出的决策边界如下效果并不好，并且输出

逻辑回归的准确性： 47 % (正确标记的数据点所占的百分比)

只有47%的准确率。

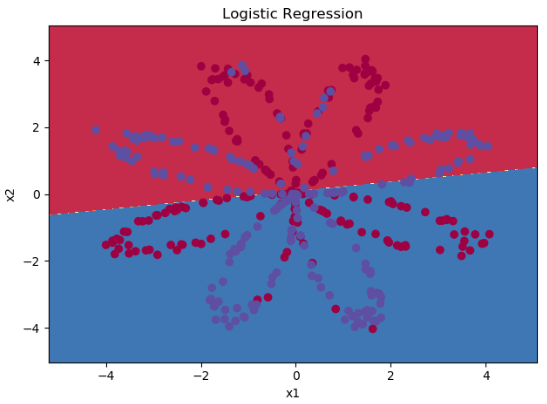
那么如果使用上一周我们学习的具有逻辑回归思维的神经网络呢？

# 使用之前写的逻辑回归思维的神经网络进行计算
from course_1_week_2.Logistic import model
d = model(X.T, Y.T, X.T, Y.T)

我们在2000次迭代后可以得到一个50%的准确率，可见这个偏置b确实可以对结果产生一定的影响。

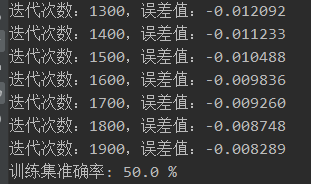
下面我们使用神经网络来进行相关的计算。

首先是初始化参数，需要随机初始化参数。

def init_parameters(n_x, n_h, n_y):
    """
    初始化参数
    :param n_x: 输入层个数
    :param n_h: 隐藏层个数
    :param n_y: 输出层个数
    :return:
    """
    # 初始化一个种子，以保证大家的结果一样
    np.random.seed(2)
    W1 = np.random.randn(n_h, n_x) * 0.01
    b1 = np.zeros((n_h, 1))
    W2 = np.random.randn(n_y, n_h) * 0.01
    b2 = np.zeros((n_y, 1))
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    assert (W1.shape == (n_h, n_x))
    assert (b1.shape == (n_h, 1))
    assert (W2.shape == (n_y, n_h))
    assert (b2.shape == (n_y, 1))
    return parameters

前向传播：

def forward_propagation(X, parameters):
    """
    前向传播
    :param X:
    :param parameters:
    :return:
    """
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    Z1 = np.dot(W1, X) + b1
    A1 = np.tanh(Z1)
    Z2 = np.dot(W2, A1) + b2
    # 这里别忘了使用sigmoid进行激活
    A2 = sigmoid(Z2)
    cache = {"Z1": Z1,
             "A1": A1,
             "Z2": Z2,
             "A2": A2}
    assert (A2.shape == (1, X.shape[1]))
    return A2, cache

计算代价，公式如下：

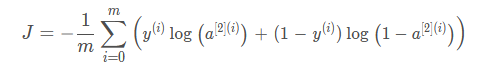
def compute_cost(A2, Y, parameters):
    """
    计算代价
    :param A2: 计算结果
    :param Y: 标签
    :param parameters: 网络参数
    :return:
    """
    m = Y.shape[1]
    if m == 0:
        print()
    # ??? 干嘛的
    W1 = parameters["W1"]
    W2 = parameters["W2"]
    # 计算成本
    logprobs = np.multiply(Y, np.log(A2)) + np.multiply((1 - Y), np.log(1 - A2))
    cost = - np.sum(logprobs) / m
    cost = float(np.squeeze(cost))
    assert (isinstance(cost, float))
    return cost

反向传播，公式如下：

def backward_propagation(parameters, cache, X, Y):
    """
    反向传播
    :param parameters:
    :param cache:
    :param X:
    :param Y:
    :return:
    """
    m = X.shape[1]

    W1 = parameters["W1"]
    W2 = parameters["W2"]

    A1 = cache["A1"]
    A2 = cache["A2"]

    dZ2 = A2 - Y
    dW2 = (1 / m) * np.dot(dZ2, A1.T)
    db2 = (1 / m) * np.sum(dZ2, axis=1, keepdims=True)
    dZ1 = np.multiply(np.dot(W2.T, dZ2), 1 - np.power(A1, 2))
    dW1 = (1 / m) * np.dot(dZ1, X.T)
    db1 = (1 / m) * np.sum(dZ1, axis=1, keepdims=True)
    grads = {"dW1": dW1,
             "db1": db1,
             "dW2": dW2,
             "db2": db2}

    return grads

计算出反向传播的值后我们就需要更新新的值，下图是不同的学习率对结果产生的影响：

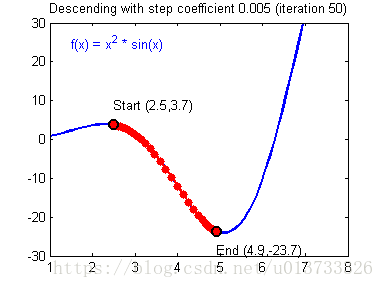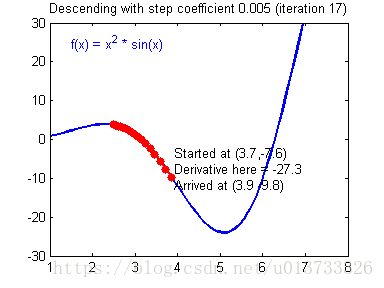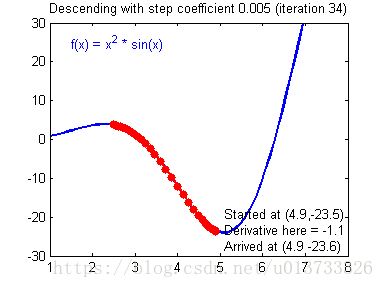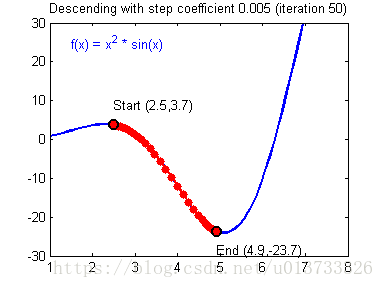
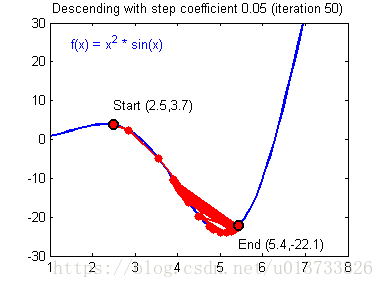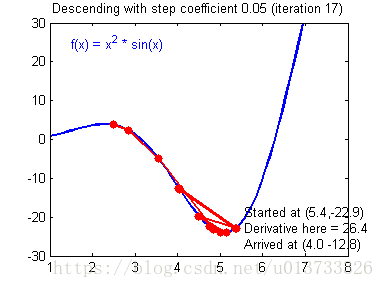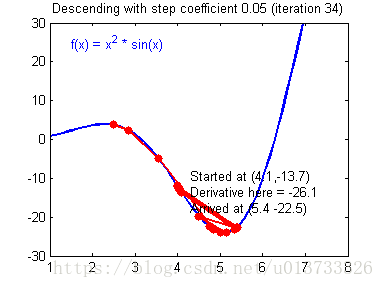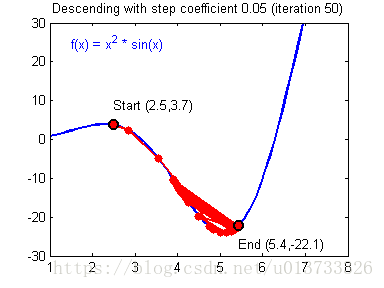
def update_parameters(parameters, grads, learning_rate=1.2):
    """
    更新权重
    :param parameters:
    :param grads:
    :param learning_rate:
    :return:
    """
    W1, W2 = parameters["W1"], parameters["W2"]
    b1, b2 = parameters["b1"], parameters["b2"]

    dW1, dW2 = grads["dW1"], grads["dW2"]
    db1, db2 = grads["db1"], grads["db2"]

    W1 = W1 - learning_rate * dW1
    b1 = b1 - learning_rate * db1
    W2 = W2 - learning_rate * dW2
    b2 = b2 - learning_rate * db2

    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}

    return parameters

预测函数：

def predict(parameters, X):
    """
    预测函数
    :param parameters:
    :param X:
    :return:
    """
    A2, cache = forward_propagation(X, parameters)
    # 四舍五入
    predictions = np.round(A2)

    return predictions

最后我们将所有的方法集合起来：

def nn_model(X, Y, n_h, num_iterations, print_cost=False):
    """
    参数：
        X - 数据集,维度为（2，示例数）
        Y - 标签，维度为（1，示例数）
        n_h - 隐藏层的数量
        num_iterations - 梯度下降循环中的迭代次数
        print_cost - 如果为True，则每1000次迭代打印一次成本数值

    返回：
        parameters - 模型学习的参数，它们可以用来进行预测。
     """

    n_x = layer_sizes(X, Y)[0]
    n_y = layer_sizes(X, Y)[2]

    parameters = init_parameters(n_x, n_h, n_y)

    for i in range(num_iterations):
        A2, cache = forward_propagation(X, parameters)
        cost = compute_cost(A2, Y, parameters)
        grads = backward_propagation(parameters, cache, X, Y)
        parameters = update_parameters(parameters, grads, learning_rate=0.5)

        if print_cost:
            if i % 1000 == 0:
                print("第 ", i, " 次循环，成本为：" + str(cost))
    return parameters

我们进行一次测试，看看使用神经网络的效果如何：

parameters = nn_model(X, Y, n_h=4, num_iterations=10000, print_cost=True)

# 绘制边界
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y[0, :])
plt.title("Decision Boundary for hidden layer size " + str(4))

predictions = predict(parameters, X)
print('准确率: %d' % float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100) + '%')
plt.show()

画出下图，并且输出准确率为90%。

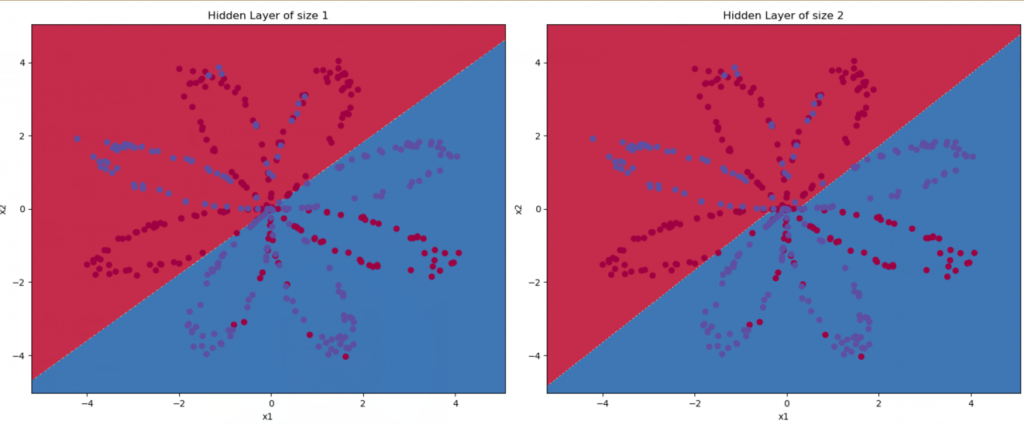
那如果我们尝试使用不同个数的隐藏层节点数呢？

plt.figure(figsize=(16, 32))
hidden_layer_sizes = [1, 2, 3, 4, 5, 20, 50]  # 隐藏层数量
for i, n_h in enumerate(hidden_layer_sizes):
    plt.subplot(5, 2, i + 1)
    plt.title('Hidden Layer of size %d' % n_h)
    parameters = nn_model(X, Y, n_h, num_iterations=10000)
    plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y[0,:])
    predictions = predict(parameters, X)
    accuracy = float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100)
    print("隐藏层的节点数量： {}  ，准确率: {} %".format(n_h, accuracy))
plt.show()

最后输出：

隐藏层的节点数量： 1  ，准确率: 67.25 %
隐藏层的节点数量： 2  ，准确率: 67.0 %
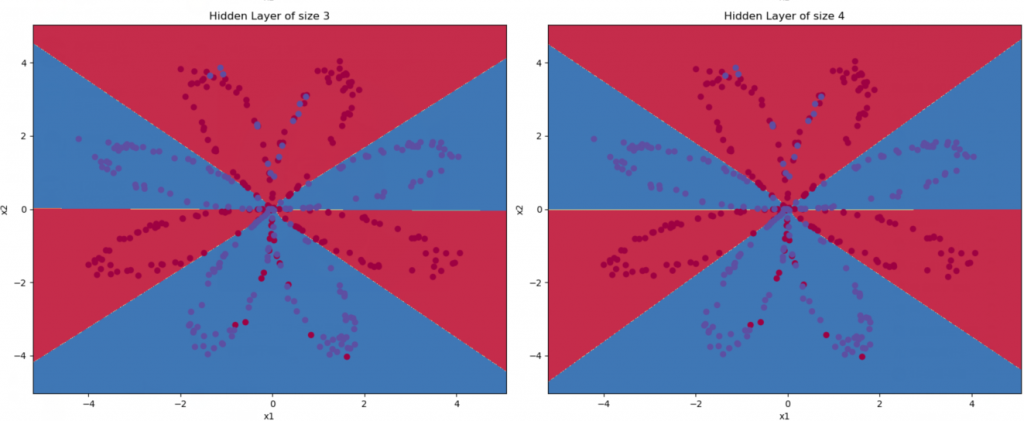
隐藏层的节点数量： 3  ，准确率: 90.75 %
隐藏层的节点数量： 4  ，准确率: 90.5 %
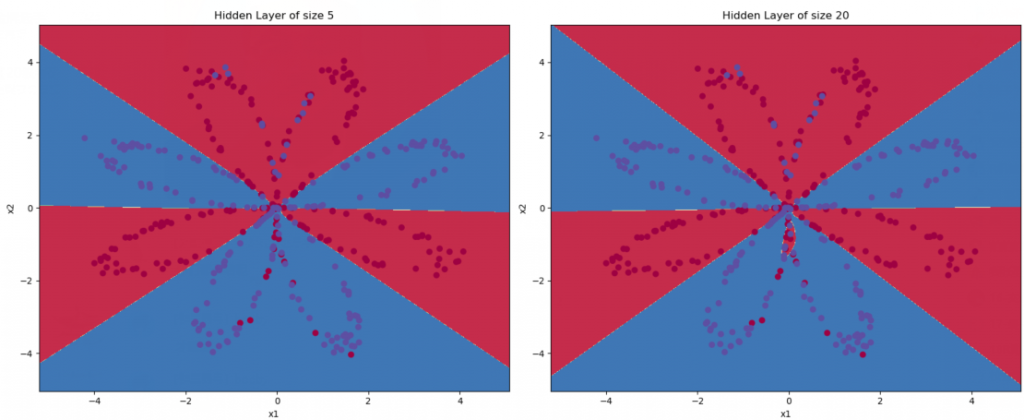
隐藏层的节点数量： 5  ，准确率: 91.0 %
隐藏层的节点数量： 20  ，准确率: 91.25 %
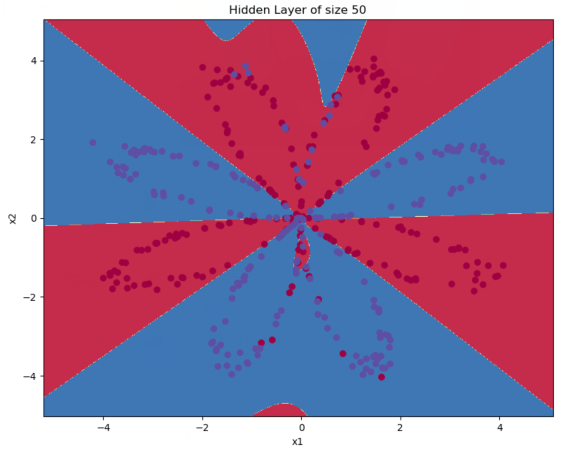
隐藏层的节点数量： 50  ，准确率: 90.75 %

并有如下图，可以看出较大的隐藏岑规模可以更好的拟合数据，有更高的准确率直至过拟合。

完整的代码如下：

# -*- coding:utf-8 -*-

import numpy as np
import matplotlib.pyplot as plt
from course_1_week_3.testCases import *
import sklearn.linear_model
from course_1_week_3.planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset, load_extra_datasets
# 加载数据
X, Y = load_planar_dataset()
print('X的维度:', X.shape)
print('Y的维度:', Y.shape)
plt.title('show point')
plt.scatter(X[0, :], X[1, :], c=Y[0, :], s=40, cmap=plt.cm.Spectral)
plt.show()
# 使用逻辑回归处理
clf = sklearn.linear_model.LogisticRegression()
clf.fit(X.T, Y.T)
# planar_util里的方法   绘制决策边界
plot_decision_boundary(lambda x: clf.predict(x), X, Y[0, :])
plt.title('Logistic Regression')
LR_predictions = clf.predict(X.T)
print("逻辑回归的准确性： %d " % float((np.dot(Y, LR_predictions) +
                               np.dot(1 - Y, 1 - LR_predictions)) / float(Y.size) * 100) +
      "% " + "(正确标记的数据点所占的百分比)")
plt.show()
# 使用之前写的逻辑回归思维的神经网络进行计算
from course_1_week_2.Logistic import model
d = model(X.T, Y.T, X.T, Y.T)
# 神经网络
# (5,3)    (2,3)
X_asses, Y_asses = layer_sizes_test_case()
def layer_sizes(X, Y):
    """
    返回神经网络各层的个数
    :param X: 输入数据集
    :param Y: 标签
    :return:
    """
    # 输入层个数
    n_x = X.shape[0]
    # 隐藏层个数
    n_h = 4
    # 输出层个数
    n_y = Y.shape[0]
    return n_x, n_h, n_y
def init_parameters(n_x, n_h, n_y):
    """
    初始化参数
    :param n_x: 输入层个数
    :param n_h: 隐藏层个数
    :param n_y: 输出层个数
    :return:
    """
    # 初始化一个种子，以保证大家的结果一样
    np.random.seed(2)
    W1 = np.random.randn(n_h, n_x) * 0.01
    b1 = np.zeros((n_h, 1))
    W2 = np.random.randn(n_y, n_h) * 0.01
    b2 = np.zeros((n_y, 1))
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    assert (W1.shape == (n_h, n_x))
    assert (b1.shape == (n_h, 1))
    assert (W2.shape == (n_y, n_h))
    assert (b2.shape == (n_y, 1))
    return parameters
def forward_propagation(X, parameters):
    """
    前向传播
    :param X:
    :param parameters:
    :return:
    """
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    Z1 = np.dot(W1, X) + b1
    A1 = np.tanh(Z1)
    Z2 = np.dot(W2, A1) + b2
    # 这里别忘了使用sigmoid进行激活
    A2 = sigmoid(Z2)
    cache = {"Z1": Z1,
             "A1": A1,
             "Z2": Z2,
             "A2": A2}
    assert (A2.shape == (1, X.shape[1]))
    return A2, cache
def compute_cost(A2, Y, parameters):
    """
    计算代价
    :param A2: 计算结果
    :param Y: 标签
    :param parameters: 网络参数
    :return:
    """
    m = Y.shape[1]
    if m == 0:
        print()
    # ??? 干嘛的
    W1 = parameters["W1"]
    W2 = parameters["W2"]
    # 计算成本
    logprobs = np.multiply(Y, np.log(A2)) + np.multiply((1 - Y), np.log(1 - A2))
    cost = - np.sum(logprobs) / m
    cost = float(np.squeeze(cost))
    assert (isinstance(cost, float))
    return cost
def backward_propagation(parameters, cache, X, Y):
    """
    反向传播
    :param parameters:
    :param cache:
    :param X:
    :param Y:
    :return:
    """
    m = X.shape[1]
    W1 = parameters["W1"]
    W2 = parameters["W2"]
    A1 = cache["A1"]
    A2 = cache["A2"]
    dZ2 = A2 - Y
    dW2 = (1 / m) * np.dot(dZ2, A1.T)
    db2 = (1 / m) * np.sum(dZ2, axis=1, keepdims=True)
    dZ1 = np.multiply(np.dot(W2.T, dZ2), 1 - np.power(A1, 2))
    dW1 = (1 / m) * np.dot(dZ1, X.T)
    db1 = (1 / m) * np.sum(dZ1, axis=1, keepdims=True)
    grads = {"dW1": dW1,
             "db1": db1,
             "dW2": dW2,
             "db2": db2}
    return grads
# 更新参数
def update_parameters(parameters, grads, learning_rate=1.2):
    """
    更新权重
    :param parameters:
    :param grads:
    :param learning_rate:
    :return:
    """
    W1, W2 = parameters["W1"], parameters["W2"]
    b1, b2 = parameters["b1"], parameters["b2"]
    dW1, dW2 = grads["dW1"], grads["dW2"]
    db1, db2 = grads["db1"], grads["db2"]
    W1 = W1 - learning_rate * dW1
    b1 = b1 - learning_rate * db1
    W2 = W2 - learning_rate * dW2
    b2 = b2 - learning_rate * db2
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    return parameters
def nn_model(X, Y, n_h, num_iterations, print_cost=False):
    """
    参数：
        X - 数据集,维度为（2，示例数）
        Y - 标签，维度为（1，示例数）
        n_h - 隐藏层的数量
        num_iterations - 梯度下降循环中的迭代次数
        print_cost - 如果为True，则每1000次迭代打印一次成本数值
    返回：
        parameters - 模型学习的参数，它们可以用来进行预测。
     """
    n_x = layer_sizes(X, Y)[0]
    n_y = layer_sizes(X, Y)[2]
    parameters = init_parameters(n_x, n_h, n_y)
    for i in range(num_iterations):
        A2, cache = forward_propagation(X, parameters)
        cost = compute_cost(A2, Y, parameters)
        grads = backward_propagation(parameters, cache, X, Y)
        parameters = update_parameters(parameters, grads, learning_rate=0.5)
        if print_cost:
            if i % 1000 == 0:
                print("第 ", i, " 次循环，成本为：" + str(cost))
    return parameters
def predict(parameters, X):
    """
    预测函数
    :param parameters:
    :param X:
    :return:
    """
    A2, cache = forward_propagation(X, parameters)
    # 四舍五入
    predictions = np.round(A2)
    return predictions
parameters = nn_model(X, Y, n_h=4, num_iterations=10000, print_cost=True)
# 绘制边界
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y[0, :])
plt.title("Decision Boundary for hidden layer size " + str(4))
predictions = predict(parameters, X)
print('准确率: %d' % float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100) + '%')
plt.show()
plt.figure(figsize=(16, 32))
hidden_layer_sizes = [1, 2, 3, 4, 5, 20, 50]  # 隐藏层数量
for i, n_h in enumerate(hidden_layer_sizes):
    plt.subplot(5, 2, i + 1)
    plt.title('Hidden Layer of size %d' % n_h)
    parameters = nn_model(X, Y, n_h, num_iterations=10000)
    plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y[0,:])
    predictions = predict(parameters, X)
    accuracy = float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100)
    print("隐藏层的节点数量： {}  ，准确率: {} %".format(n_h, accuracy))
plt.show()
"""
隐藏层的节点数量： 1  ，准确率: 67.25 %
隐藏层的节点数量： 2  ，准确率: 67.0 %
隐藏层的节点数量： 3  ，准确率: 90.75 %
隐藏层的节点数量： 4  ，准确率: 90.5 %
隐藏层的节点数量： 5  ，准确率: 91.0 %
隐藏层的节点数量： 20  ，准确率: 91.25 %
隐藏层的节点数量： 50  ，准确率: 90.75 %
"""