【吴恩达深度学习】深度神经网络

吴恩达深度学习第一课第四周 深度学习网络

1.什么是深层神经网络

如下图，分别是逻辑回归，有一个隐藏层的神经网络，有两个隐藏层的神经网络，有五个隐藏层的神经网络。

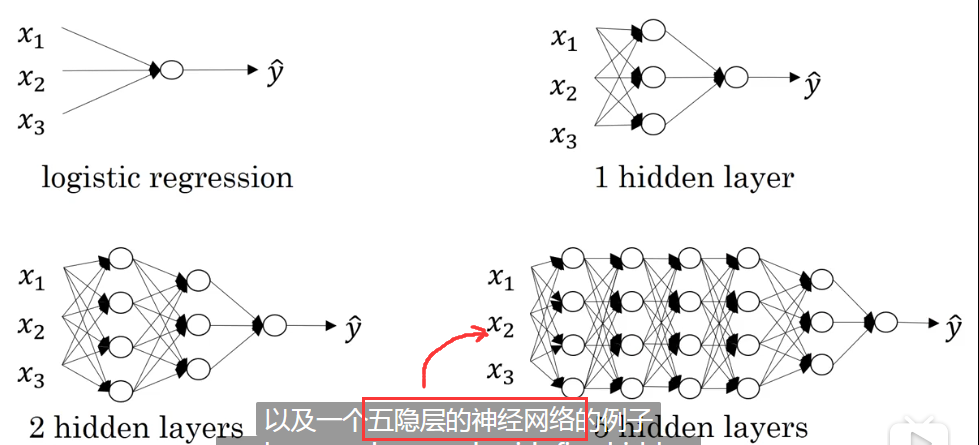
我们一般称有一个以上隐藏层的网络为深层神经网络。

我们在选择模型的时候，一般先使用逻辑回归，然后双层神经网络、三层神经网络以此类推，把隐藏层层数作为一个可以自由选择大小的超参来改变。

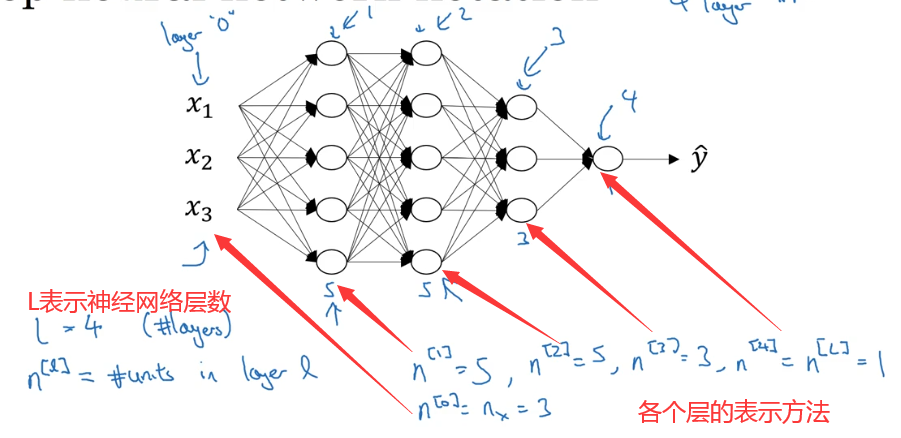
2. 深层神经网络的符号表示

和普通的神经网络表示基本一样，点了个层数L。

3.参数VS超参

之后我们我们还会接触一些其他的超参，比如monmentum、mini batch size、不同的正则化参数等等。

测验

1. 在实现前向传播和反向传播中使用的“cache”是什么？

1. 用于在训练期间缓存成本函数的中间值。
2. 我们用它传递前向传播中计算的变量到相应的反向传播步骤，它包含用于计算导数的反向传播的有用值。
3. 它用于跟踪我们正在搜索的超参数，以加速计算。
4. 我们使用它将向后传播计算的变量传递给相应的正向传播步骤，它包含用于计算计算激活的正向传播的有用值。

2。

2. 以下哪些是“超参数”？

1. 隐藏层的大小n[l]
2. 学习率α
3. 迭代次数
4. 神经网络中的层数L

1、2、3、4。

3.下列哪个说法是正确的？

1. 神经网络的更深层通常比前面的层计算更复杂的输入特征。
2. 神经网络的前面的层通常比更深层计算输入的更复杂的特性。

1。

4. 向量化允许您在L层神经网络中计算前向传播，而不需要在层(l = 1,2，…，L)上显式的使用for-loop（或任何其他显式迭代循环），正确吗？

错误。 层间计算中，我们不能避免for循环迭代。

5. 假设我们将n[l]的值存储在名为layers的数组中，如下所示：layer_dims = [n_x,4,3,2,1]。 因此，第1层有四个隐藏单元，第2层有三个隐藏单元，依此类推。 您可以使用哪个for循环初始化模型参数？

for(i in range(1, len(layer_dims))):
     parameter[‘W’ + str(i)] = np.random.randn(layers[i], layers[i - 1])) * 0.01
     parameter[‘b’ + str(i)] = np.zeros((layers_dims[l], 1))

6. 层数L为4，隐藏层数为3正确么？

正确。

7. 在前向传播期间，在层l的前向传播函数中，您需要知道层l中的激活函数（Sigmoid，tanh，ReLU等）是什么， 在反向传播期间，相应的反向传播函数也需要知道第l层的激活函数是什么，因为梯度是根据它来计算的，正确吗？

正确。反向传播中需要知道使用哪种激活函数才能正确的计算导函数。

8.使用浅网络电路计算函数时，需要一个大网络（我们通过网络中的逻辑门数量来度量大小），但是使用深网络电路来计算它，只需要一个指数较小的网络。真/假？

正确。

编程作业

步骤：

1.初始化网络参数

2.前向传播

2.1 计算一层的中线性求和的部分

2.2 计算激活函数的部分（ReLU使用L-1次，Sigmod使用1次）

2.3 结合线性求和与激活函数

3.计算误差

4.反向传播

4.1 线性部分的反向传播公式

4.2 激活函数部分的反向传播公式

4.3 结合线性部分与激活函数的反向传播公式

5.更新参数

首先我们导包：

import numpy as np
import h5py
import matplotlib.pyplot as plt
from course_1_week_4 import testCases
from course_1_week_4.dnn_utils import sigmoid, sigmoid_backward, relu, relu_backward
from course_1_week_4 import lr_utils

在这一课，实现两种神经网络，一个是上一周的双层神经网络，一个是这一周的深层神经网络，因此我们首先写一个对双层神经网络的参数初始化方法：

def init_two_layer_parameters(n_x, n_h, n_y):
    """
    随机初始化参数（一个两层的神经网络）
    :param n_x: 输入层结点个数
    :param n_h: 隐藏层结点个数
    :param n_y: 输出层结点个数
    :return:
    """
    W1 = np.random.randn(n_h, n_x) * 0.01
    b1 = np.zeros((n_h, 1))
    W2 = np.random.randn(n_y, n_h) * 0.01
    b2 = np.zeros((n_y, 1))

    parameters = {
        'W1': W1,
        'b1': b1,
        'W2': W2,
        'b2': b2
    }
    return parameters

同样在写一个深层神经网络的参数初始化（当然，深层可以初始化两层的）：

def init_deep_layers_parameters(layers_dim):
    """
    初始化多层神经网络参数
    :param layers_dim: 每层节点数的列表
    :return:
    """
    parameters = {}
    for i in range(1, len(layers_dim)):
        parameters['W' + str(i)] = np.random.randn(layers_dim[i], layers_dim[i - 1]) * 0.01
        parameters['b' + str(i)] = np.zeros((layers_dim[i], 1))

    return parameters

完成了参数的初始化我们就开始进行前向传播相关的代码。

首先是线性传播的方法，只计算wx+b而不进行激活，同时将A,W,b作为缓存返回

def linear_forward(A, W, b):
    """
    前向传播（只算wx+b，不激活）
    :param A:
    :param W:
    :param b:
    :return:
    """
    Z = np.dot(W, A) + b
    cache = (A, W, b)
    return Z, cache

然后是激活函数，在这里进行分类，因为我们二分类的神经网络最后一层使用的是sigmoid激活，而在这之前我们都在使用ReLU进行激活。同时将激活前的结果和x、w、b作为缓存返回（x因为是当前层的结果，下一层的输入，在计算下一层的时候和反向传播时需要用到，因此缓存。另外两个本身就是参数，必然缓存）。

def linear_activation_forward(A_prev, W, b, activation):
    """
    前向传播的激活
    :param A_prev:上一层的激活值
    :param W:
    :param b:
    :param activation: 激活函数
    :return:
    """
    assert activation in ['sigmoid', 'relu']
    Z, linear_cache = linear_forward(A_prev, W, b)
    if activation is 'sigmoid':
        A, activation_cache = sigmoid(Z)
    else:
        A, activation_cache = relu(Z)

    #    进行xw+b(按顺序)的各个参数  # 进行激活的Z
    cache = linear_cache, activation_cache
    return A, cache

到这里，我们可以实现一次神经网络的前向传播，那我们需要写深层的传播，也就是进行n次单层的传播调用（这里多缓存了激活前的z，而之前使用sigmoid时没有缓存，一个原因是sigmoid函数的导数依然有sigmoid函数，可以用激活后的A进行计算，而ReLU却没有，因此需要Z来充当复合函数求导后的x项）

def L_model_forward(X, parameters):
    """
    多层模型的传播
    :param X:
    :param parameters:
    :return:
    """
    caches = []
    A = X
    L = len(parameters) // 2
    for i in range(1, L):
        A, cache = linear_activation_forward(A, parameters['W' + str(i)], parameters['b' + str(i)], 'relu')
        caches.append(cache)
    AL, cahce = linear_activation_forward(A, parameters['W' + str(L)], parameters['b' + str(L)], 'sigmoid')
    # caches 中为 每一次传播过程的（进行xw+b的各个参数，进行激活的Z）
    caches.append(cahce)

    return AL, caches

我们进行完了前向传播然后计算代价

def compute_cost(AL, Y):
    """
    计算成本
    :param AL:
    :param Y:
    :return:
    """
    m = Y.shape[1]
    cost = -np.sum(np.multiply(np.log(AL), Y) + np.multiply(np.log(1 - AL), 1 - Y)) / m

    # 矩阵转数组(单个数字)
    cost = np.squeeze(cost)
    return cost

然后进行反向传播，首先是计算误差，当然也是只计算一轮。

def linear_backward(dZ, cache):
    """
    反向传播
    :param dZ:
    :param cache:
    :return:
    """
    A_prev, W, b = cache
    m = A_prev.shape[1]
    dW = np.dot(dZ, A_prev.T) / m
    db = np.sum(dZ, axis=1, keepdims=True) / m
    dA_prev = np.dot(W.T, dZ)

    return dA_prev, dW, db

然后是激活函数部分，一样，根据前向传播时使用的不同激活函数进行激活：

def linear_activation_backward(dA, cache, activation='relu'):
    """
    反向传播的激活
    :param dA:
    :param cache:
    :param activation:
    :return:
    """
    assert activation in ['sigmoid', 'relu']
    linear_cache, activation_cache = cache
    if activation is "relu":
        dZ = relu_backward(dA, activation_cache)
        dA_prev, dW, db = linear_backward(dZ, linear_cache)
    elif activation is "sigmoid":
        dZ = sigmoid_backward(dA, activation_cache)
        dA_prev, dW, db = linear_backward(dZ, linear_cache)
    return dA_prev, dW, db

然后是L层进行反向传播：

def L_model_backward(AL, Y, caches):
    """
    多层网络的反向传播
    :param AL:
    :param Y:
    :param caches:
    :return:
    """
    grads = {}
    L = len(caches)
    Y = Y.reshape(AL.shape)
    dAL = -(np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))

    current_cache = caches[-1]
    grads['dA' + str(L)], grads['dW' + str(L)], grads['db' + str(L)] = linear_activation_backward(dAL, current_cache,
                                                                                                  'sigmoid')
    for l in range(L - 1):
        current_cache = caches[l]
        dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads['dA' + str(l + 2)], current_cache, 'relu')
        grads['dA' + str(l + 1)] = dA_prev_temp
        grads['dW' + str(l + 1)] = dW_temp
        grads['db' + str(l + 1)] = db_temp

    return grads

更新参数：

def update_parameters(parameters, grads, learning_rate):
    """
    更新参数
    :param parameters:
    :param grads:
    :param learning_rate:
    :return:
    """
    L = len(parameters) // 2
    for i in range(L):
        parameters['W' + str(i + 1)] = parameters['W' + str(i + 1)] - learning_rate * grads['dW' + str(i + 1)]
        parameters['b' + str(i + 1)] = parameters['b' + str(i + 1)] - learning_rate * grads['db' + str(i + 1)]

    return parameters

预测结果的预测函数：

def predict(X, y, parameters):
    """
    预测结果
    :param X:
    :param y:
    :param parameters:
    :return:
    """
    m = X.shape[1]
    p = np.zeros((1, m))

    # 根据参数前向传播
    probas, caches = L_model_forward(X, parameters)

    for i in range(0, probas.shape[1]):
        if probas[0, i] > 0.5:
            p[0, i] = 1
        else:
            p[0, i] = 0

    print("准确度为: " + str(float(np.sum((p == y)) / m)))
    return p

然后是神经网络模型，将上面所有的方法串起来使用（方法名是两层网络，但是多层实现依然在里面，只要将注释解开，改变laters_dims的值就可以变成深层网络）：

def two_layer_model(X, Y, layers_dims, learning_rate=0.0075, num_iterations=3000, print_cost=False, isPlot=True):
    """
    实现一个两层的神经网络
    :param X:
    :param Y:
    :param layers_dims:
    :param learning_rate:
    :param num_iteration:
    :param print_cost:
    :param isPlot:
    :return:
    """
    np.random.seed(1)

    grads = {}
    costs = []
    n_x, n_h, n_y = layers_dims

    parameters = init_two_layer_parameters(n_x, n_h, n_y)
    # parameters = init_deep_layers_parameters(layers_dims)

    W1 = parameters['W1']
    W2 = parameters['W2']
    b1 = parameters['b1']
    b2 = parameters['b2']

    for i in range(num_iterations):
        # 前向传播
        A1, cache1 = linear_activation_forward(X, W1, b1, 'relu')
        A2, cache2 = linear_activation_forward(A1, W2, b2, 'sigmoid')
        # A2, caches = L_model_forward(X, parameters)

        cost = compute_cost(A2, Y)

        # 反向传播
        dA2 = - (np.divide(Y, A2) - np.divide(1 - Y, 1 - A2))
        dA1, dW2, db2 = linear_activation_backward(dA2, cache2, "sigmoid")
        dA0, dW1, db1 = linear_activation_backward(dA1, cache1, "relu")
        # grads = L_model_backward(A2, Y, caches)

        # 向后传播完成后的数据保存到grads
        grads["dW1"] = dW1
        grads["db1"] = db1
        grads["dW2"] = dW2
        grads["db2"] = db2

        # 更新参数
        parameters = update_parameters(parameters, grads, learning_rate)
        W1 = parameters["W1"]
        b1 = parameters["b1"]
        W2 = parameters["W2"]
        b2 = parameters["b2"]

        # 打印成本值，如果print_cost=False则忽略
        if i % 100 == 0:
            # 记录成本
            costs.append(cost)
            # 是否打印成本值
            if print_cost:
                print("第", i, "次迭代，成本值为：", np.squeeze(cost))
    # 迭代完成，根据条件绘制图
    if isPlot:
        plt.plot(np.squeeze(costs))
        plt.ylabel('cost')
        plt.xlabel('iterations (per tens)')
        plt.title("Learning rate =" + str(learning_rate))
        plt.show()
    # 返回parameters
    return parameters

最后读取数据集与标准化，调用网络模型：

# 预处理数据集
train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes = lr_utils.load_dataset()

train_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0], -1).T
test_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T

# RGB标准化
train_x = train_x_flatten / 255
train_y = train_set_y
test_x = test_x_flatten / 255
test_y = test_set_y

n_x = 12288
n_h = 7
n_y = 1
layers_dims = (n_x, n_h, n_y)

parameters = two_layer_model(train_x, train_set_y, layers_dims=(n_x, n_h, n_y), num_iterations=2500, print_cost=True,
                             isPlot=True)

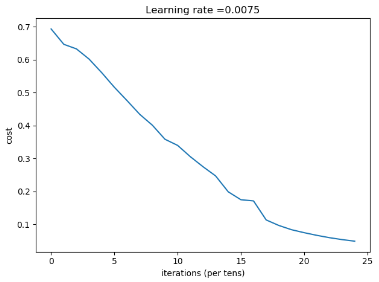
结果：

第 2300 次迭代，成本值为： 0.05336140348560556
第 2400 次迭代，成本值为： 0.048554785628770185
准确度为: 1.0
准确度为: 0.72

生成图像：

上面是使用双层参数初始化，按说使用多层参数初始化对结果不会构成很大影响，但是实际上结果如下：

第 2300 次迭代，成本值为： 0.14781357997051983
第 2400 次迭代，成本值为： 0.12935258942424563
准确度为: 1.0
准确度为: 0.74

虽然代价变高了，但是准确度却上升了。

我们查看一下识别失败的图片：

def print_mislabeled_images(classes, X, y, p):
    """
   绘制预测和实际不同的图像。
       X - 数据集
       y - 实际的标签
       p - 预测
    """
    a = p + y
    mislabeled_indices = np.asarray(np.where(a == 1))
    plt.rcParams['figure.figsize'] = (40.0, 40.0)  # set default size of plots
    num_images = len(mislabeled_indices[0])
    for i in range(num_images):
        index = mislabeled_indices[1][i]

        plt.subplot(2, num_images, i + 1)
        plt.imshow(X[:, index].reshape(64, 64, 3), interpolation='nearest')
        plt.axis('off')
        plt.title(
            "Prediction: " + classes[int(p[0, index])].decode("utf-8") + " \n Class: " + classes[y[0, index]].decode(
                "utf-8"))
    plt.show()


print_mislabeled_images(classes, test_x, test_y, pred_test)

发现确实有一些不是猫，但是有一些姿势千奇百怪的猫依然没有办法进行识别。

完整代码：

# -*- coding:utf-8 -*-

"""
      ┏┛ ┻━━━━━┛ ┻┓
      ┃　　　　　　 ┃
      ┃　　　━　　　┃
      ┃　┳┛　  ┗┳　┃
      ┃　　　　　　 ┃
      ┃　　　┻　　　┃
      ┃　　　　　　 ┃
      ┗━┓　　　┏━━━┛
        ┃　　　┃   神兽保佑
        ┃　　　┃   代码无BUG！
        ┃　　　┗━━━━━━━━━┓
        ┃　　　　　　　    ┣┓
        ┃　　　　         ┏┛
        ┗━┓ ┓ ┏━━━┳ ┓ ┏━┛
          ┃ ┫ ┫   ┃ ┫ ┫
          ┗━┻━┛   ┗━┻━┛
"""

import numpy as np
import h5py
import matplotlib.pyplot as plt
from course_1_week_4 import testCases
from course_1_week_4.dnn_utils import sigmoid, sigmoid_backward, relu, relu_backward
from course_1_week_4 import lr_utils

# 指定随机数种子
np.random.seed(1)


def init_two_layer_parameters(n_x, n_h, n_y):
    """
    随机初始化参数（一个两层的神经网络）
    :param n_x: 输入层结点个数
    :param n_h: 隐藏层结点个数
    :param n_y: 输出层结点个数
    :return:
    """
    W1 = np.random.randn(n_h, n_x) * 0.01
    b1 = np.zeros((n_h, 1))
    W2 = np.random.randn(n_y, n_h) * 0.01
    b2 = np.zeros((n_y, 1))

    parameters = {
        'W1': W1,
        'b1': b1,
        'W2': W2,
        'b2': b2
    }
    return parameters


def init_deep_layers_parameters(layers_dim):
    """
    初始化多层神经网络参数
    :param layers_dim: 每层节点数的列表
    :return:
    """
    parameters = {}
    for i in range(1, len(layers_dim)):
        parameters['W' + str(i)] = np.random.randn(layers_dim[i], layers_dim[i - 1]) * 0.01
        parameters['b' + str(i)] = np.zeros((layers_dim[i], 1))

    return parameters


def linear_forward(A, W, b):
    """
    前向传播（只算wx+b，不激活）
    :param A:
    :param W:
    :param b:
    :return:
    """
    Z = np.dot(W, A) + b
    cache = (A, W, b)
    return Z, cache


def linear_activation_forward(A_prev, W, b, activation):
    """
    前向传播的激活
    :param A_prev:上一层的激活值
    :param W:
    :param b:
    :param activation: 激活函数
    :return:
    """
    assert activation in ['sigmoid', 'relu']
    Z, linear_cache = linear_forward(A_prev, W, b)
    if activation is 'sigmoid':
        A, activation_cache = sigmoid(Z)
    else:
        A, activation_cache = relu(Z)

    #    进行xw+b(按顺序)的各个参数  # 进行激活的Z
    cache = linear_cache, activation_cache
    return A, cache


def L_model_forward(X, parameters):
    """
    多层模型的传播
    :param X:
    :param parameters:
    :return:
    """
    caches = []
    A = X
    L = len(parameters) // 2
    for i in range(1, L):
        A, cache = linear_activation_forward(A, parameters['W' + str(i)], parameters['b' + str(i)], 'relu')
        caches.append(cache)
    AL, cahce = linear_activation_forward(A, parameters['W' + str(L)], parameters['b' + str(L)], 'sigmoid')
    # caches 中为 每一次传播过程的（进行xw+b的各个参数，进行激活的Z）
    caches.append(cahce)

    return AL, caches


def compute_cost(AL, Y):
    """
    计算成本
    :param AL:
    :param Y:
    :return:
    """
    m = Y.shape[1]
    cost = -np.sum(np.multiply(np.log(AL), Y) + np.multiply(np.log(1 - AL), 1 - Y)) / m

    # 矩阵转数组(单个数字)
    cost = np.squeeze(cost)
    return cost


def linear_backward(dZ, cache):
    """
    反向传播
    :param dZ:
    :param cache:
    :return:
    """
    A_prev, W, b = cache
    m = A_prev.shape[1]
    dW = np.dot(dZ, A_prev.T) / m
    db = np.sum(dZ, axis=1, keepdims=True) / m
    dA_prev = np.dot(W.T, dZ)

    return dA_prev, dW, db


def linear_activation_backward(dA, cache, activation='relu'):
    """
    反向传播的激活
    :param dA:
    :param cache:
    :param activation:
    :return:
    """
    assert activation in ['sigmoid', 'relu']
    linear_cache, activation_cache = cache
    if activation is "relu":
        dZ = relu_backward(dA, activation_cache)
        dA_prev, dW, db = linear_backward(dZ, linear_cache)
    elif activation is "sigmoid":
        dZ = sigmoid_backward(dA, activation_cache)
        dA_prev, dW, db = linear_backward(dZ, linear_cache)

    return dA_prev, dW, db


def L_model_backward(AL, Y, caches):
    """
    多层网络的反向传播
    :param AL:
    :param Y:
    :param caches:
    :return:
    """
    grads = {}
    L = len(caches)
    Y = Y.reshape(AL.shape)
    dAL = -(np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))

    current_cache = caches[-1]
    grads['dA' + str(L)], grads['dW' + str(L)], grads['db' + str(L)] = linear_activation_backward(dAL, current_cache,
                                                                                                  'sigmoid')
    for l in reversed(range(L-1)):
        current_cache = caches[l]
        dA_prev_temp, dW_temp, db_temp = linear_activation_backward(grads['dA' + str(l + 2)], current_cache, 'relu')
        grads['dA' + str(l + 1)] = dA_prev_temp
        grads['dW' + str(l + 1)] =
 dW_temp
        grads['db' + str(l + 1)] = db_temp

    return grads


def update_parameters(parameters, grads, learning_rate):
    """
    更新参数
    :param parameters:
    :param grads:
    :param learning_rate:
    :return:
    """
    L = len(parameters) // 2
    for i in range(L):
        parameters['W' + str(i + 1)] = parameters['W' + str(i + 1)] - learning_rate * grads['dW' + str(i + 1)]
        parameters['b' + str(i + 1)] = parameters['b' + str(i + 1)] - learning_rate * grads['db' + str(i + 1)]

    return parameters


def two_layer_model(X, Y, layers_dims, learning_rate=0.0075, num_iterations=3000, print_cost=False, isPlot=True):
    """
    实现一个两层的神经网络
    :param X:
    :param Y:
    :param layers_dims:
    :param learning_rate:
    :param num_iteration:
    :param print_cost:
    :param isPlot:
    :return:
    """
    np.random.seed(1)

    grads = {}
    costs = []
    # n_x, n_h, n_y = layers_dims

    # parameters = init_two_layer_parameters(n_x, n_h, n_y)
    parameters = init_deep_layers_parameters(layers_dims)

    W1 = parameters['W1']
    W2 = parameters['W2']
    b1 = parameters['b1']
    b2 = parameters['b2']

    for i in range(num_iterations):
        # 前向传播
        # A1, cache1 = linear_activation_forward(X, W1, b1, 'relu')
        # A2, cache2 = linear_activation_forward(A1, W2, b2, 'sigmoid')
        AL, caches = L_model_forward(X, parameters)

        cost = compute_cost(AL, Y)

        # 反向传播
        # dA2 = - (np.divide(Y, A2) - np.divide(1 - Y, 1 - A2))
        # dA1, dW2, db2 = linear_activation_backward(dA2, cache2, "sigmoid")
        # dA0, dW1, db1 = linear_activation_backward(dA1, cache1, "relu")
        grads = L_model_backward(AL, Y, caches)

        # 向后传播完成后的数据保存到grads
        # grads["dW1"] = dW1
        # grads["db1"] = db1
        # grads["dW2"] = dW2
        # grads["db2"] = db2

        # 更新参数
        parameters = update_parameters(parameters, grads, learning_rate)
        # W1 = parameters["W1"]
        # b1 = parameters["b1"]
        # W2 = parameters["W2"]
        # b2 = parameters["b2"]

        # 打印成本值，如果print_cost=False则忽略
        if i % 100 == 0:
            # 记录成本
            costs.append(cost)
            # 是否打印成本值
            if print_cost:
                print("第", i, "次迭代，成本值为：", np.squeeze(cost))
    # 迭代完成，根据条件绘制图
    if isPlot:
        plt.plot(np.squeeze(costs))
        plt.ylabel('cost')
        plt.xlabel('iterations (per tens)')
        plt.title("Learning rate =" + str(learning_rate))
        plt.show()
    # 返回parameters
    return parameters


def predict(X, y, parameters):
    """
    预测结果
    :param X:
    :param y:
    :param parameters:
    :return:
    """
    m = X.shape[1]
    p = np.zeros((1, m))

    # 根据参数前向传播
    probas, caches = L_model_forward(X, parameters)

    for i in range(0, probas.shape[1]):
        if probas[0, i] > 0.5:
            p[0, i] = 1
        else:
            p[0, i] = 0

    print("准确度为: " + str(float(np.sum((p == y)) / m)))
    return p


# 预处理数据集
train_set_x_orig, train_set_y, test_set_x_orig, test_set_y, classes = lr_utils.load_dataset()

train_x_flatten = train_set_x_orig.reshape(train_set_x_orig.shape[0], -1).T
test_x_flatten = test_set_x_orig.reshape(test_set_x_orig.shape[0], -1).T

# RGB标准化
train_x = train_x_flatten / 255
train_y = train_set_y
test_x = test_x_flatten / 255
test_y = test_set_y

n_x = 12288
n_h = 7
n_y = 1
layers_dims = (n_x, n_h, n_y)

parameters = two_layer_model(train_x, train_set_y, layers_dims=(n_x, n_h, n_y), num_iterations=2500, print_cost=True,
                             isPlot=True)
"""
cost： 0.05336140348560556
cost： 0.048554785628770185
train准确度为: 1.0
test准确度为: 0.72

cost为： 0.14781357997051983
cost： 0.12935258942424563
train准确度为: 1.0
test准确度为: 0.74
"""

pred_train = predict(train_x, train_y, parameters)
pred_test = predict(test_x, test_y, parameters)


def print_mislabeled_images(classes, X, y, p):
    """
   绘制预测和实际不同的图像。
       X - 数据集
       y - 实际的标签
       p - 预测
    """
    a = p + y
    mislabeled_indices = np.asarray(np.where(a == 1))
    plt.rcParams['figure.figsize'] = (40.0, 40.0)  # set default size of plots
    num_images = len(mislabeled_indices[0])
    for i in range(num_images):
        index = mislabeled_indices[1][i]

        plt.subplot(2, num_images, i + 1)
        plt.imshow(X[:, index].reshape(64, 64, 3), interpolation='nearest')
        plt.axis('off')
        plt.title(
            "Prediction: " + classes[int(p[0, index])].decode("utf-8") + " \n Class: " + classes[y[0, index]].decode(
                "utf-8"))
    plt.show()


print_mislabeled_images(classes, test_x, test_y, pred_test)