吴恩达深度学习第二课第一周 深度学习的实用层面

本周我们将学习超参数的调优 如何构建数据 如何确保优化算法快速运行。
1.数据的划分
数据集的科学划分往往可以提高网络的准确率以及评价的中肯性。
机器学习时代,如果我们不设置验证集,那么一般训练集占70%,测试集栈30%;如果我们设置验证集,那他们的比例一般为60%,20%,20%。当然这并不绝对,如果我们有100万条数据,那么我们98万条训练集、验证集和测试集各1万条也是可以的。
对于现代深度学习,如果我们的数据来源十分复杂的情况,比如有一些精美处理过的数据,有一些爬取来的差一些的数据,这时候训练集、验证集以及测试集中各种质量的数据比例要基本一致。当然对于不需要对结果做出无错验证的情况也可以不使用测试集(当然这时候你可以称验证集为测试集)。
2.偏差&方差
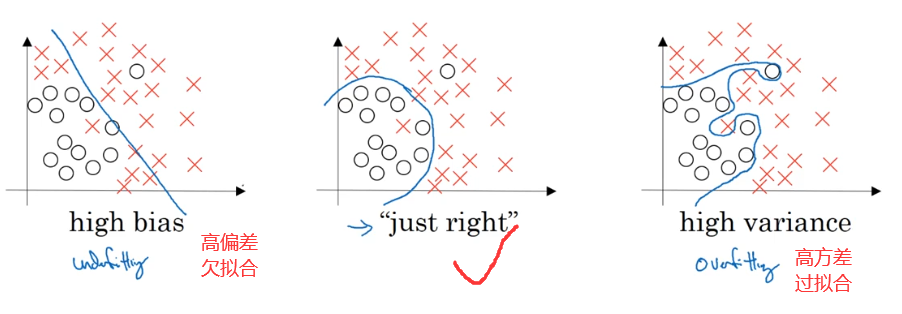
对于高偏差和高方差在错误率上的体现如下表所示:

3.机器学习基础
详见 机器学习算法与调优。
4.正则化
如果欠拟合我们往往需要增大数据量,但是如果很难再增加数据量或者获取数据的代价很高,我们可以使用正则化来减少网络的误差和防止过拟合。
正则化其实就是限制权重的变化速度。
L2正则化:实际上就是多加了一个权重矩阵的二范数的平方。 ( 目的是让权重更加接近原点,其他叫法也有岭回归或者Tikhonov正则)
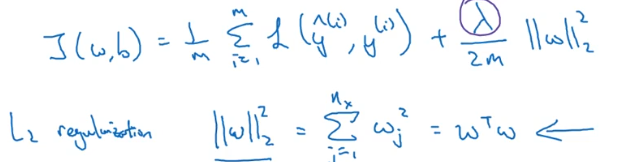
L1正则化:相比L2正则,L1正则会产生更加稀疏的解。一般被用来特征选择机制。
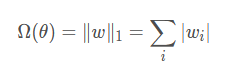
5.Dropout正则化
还有一个非常有效的正则化方法:dropout(随机失活)。
5.1反向随机失活
我们设置一个keep_prob参数,假设值为0.8,那么意味着这个神经网络将会有20%的神经元被消去,80%神经元被保留。
3 = np.random.rand(a3.shape[0], a3.shape[1]) < keep.prob所有小于该值的神经元都会被置为0,其余置为1。
a3 = np.multiply(a3, d3)
a3 /= keep_prob除以keep_prob它会大致矫正或者补足你丢失的20%,以确保a3的期望值仍然维持在同一水准。这也会使你在测试时轻松一点,因为你没有增加额外的缩放问题(scaling problem)。
测试时我们不需要执行Dropout操作,你没有必要随机化你的输出。如果你在测试阶段使用了Dropout,那只会增加你预测上的噪音。理论上,你可以多次用不用的隐藏单元运行随机化的Dropout,但也只会给你不用Dropout一样的结果。这会耗费了你的计算效率,但给了你同样的结果。
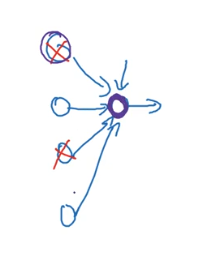
如下图,实际上dropout做的事情是使结果不会过分依赖与某一个结点,因为他们都会随机失效,也就防止了过拟合的发生,一般用在计算机视觉上偏多,因为网络常常有过拟合的问题。
6.其他正则化
early stop
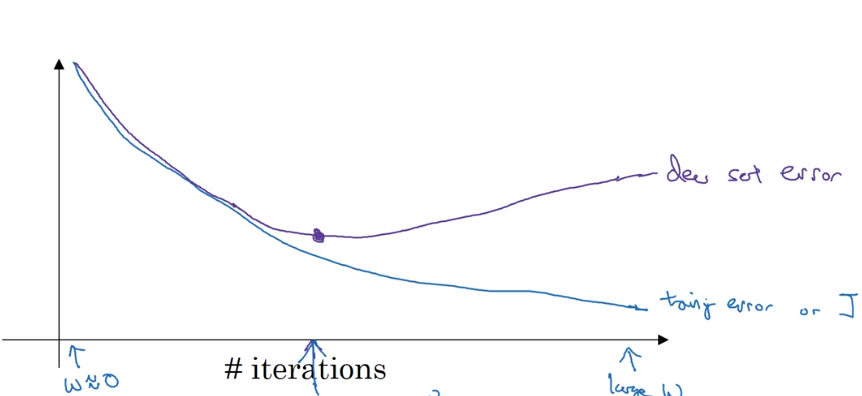
由于刚开始初始化的时候w很小,随着迭代的次数通过观察训练集代价和验证集代价,当发现验证集代价开始升高的时候,说明接下来的迭代就可能是开始对训练集进行过拟合了,这时候早早的结束算法获得的往往是一个比较好的结果。
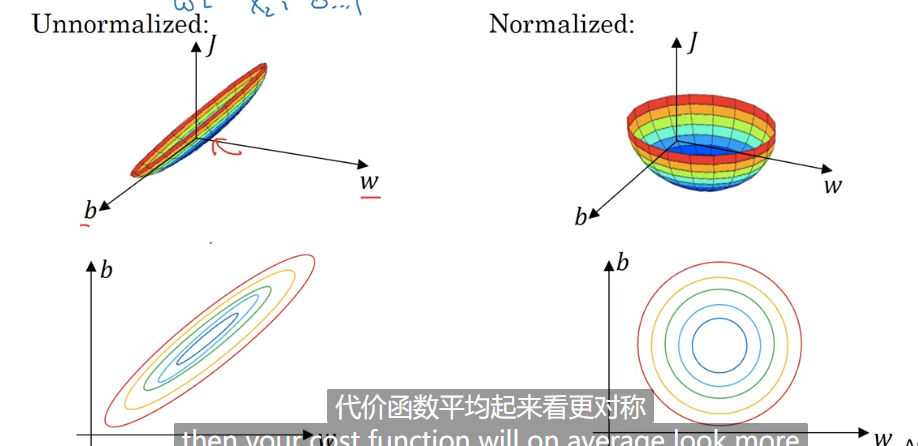
7.归一化输入
标准化训练集
将训练集的值均匀的散列在远点附近(类似于做正态分布)。
8.梯度消失和梯度爆炸
梯度消失是在使用例如sigmoid激活函数这类,当结果较大或者较小时,导数趋近于0,这样在传播的时候,随着网络的加深,z的绝对值变大,导数开始趋近于0,这样反向传播的时候无法被快速更新,导致神经网络无法被快速优化甚至永远不会收敛。
梯度爆炸则相反,随着网络的越来越深,w的值越老越大,可能会导致一个非常大的权重更新。
对于梯度消失的解决办法通常更好的参数初始化、使用ReLU代替Sigmoid等,而解决梯度爆炸的方法可以有梯度阶段、更快的优化器或者使用LSTM等。
9.梯度的数值逼近(双边误差公式)
双边误差就是更改一下求导方法,以达到更优秀的精度。
具体推导如下:
我们知道导数的定义
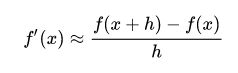
使用泰勒展开的话如下
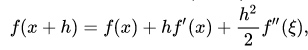
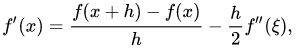
我们可以得出误差项与h同阶。
如果我们使用两个导数
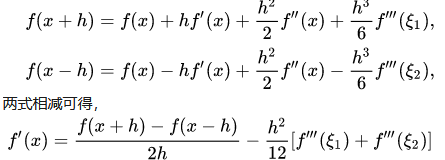
我们发现现在的误差项变为h方同阶,精度得到了提升。
10.梯度检验
神经网络算法使用反向传播计算目标函数关于每个参数的梯度,可以看做解析梯度。由于计算过程中涉及到的参数很多,反向传播计算的梯度很容易出现误差,导致最后迭代得到效果很差的参数值。
为了确认代码中反向传播计算的梯度是否正确,可以采用梯度检验(gradient check)的方法。通过计算数值梯度,得到梯度的近似值,然后和反向传播得到的梯度进行比较,若两者相差很小的话则证明反向传播的代码是正确无误的。
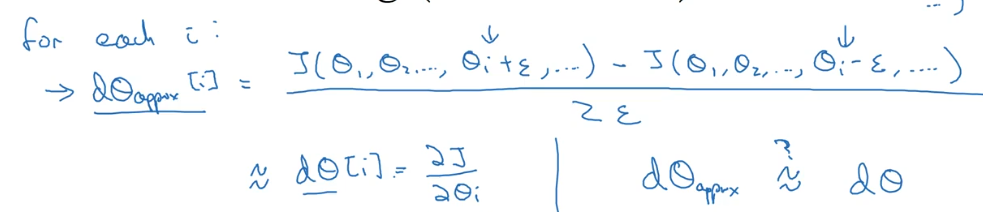
一般我们认为差距10^-7是比较好的,10^-5一般,可能产生bug,而10^-3可能就要仔细检查有没有bug的产生。
需要注意的是:
- 不要在训练中使用梯度检验,仅仅是在调试阶段使用,因为它太慢了
- 如果检验不合格,要检查每一项的值以确定bug的位置
- 在实施梯度检验的时候不要忘记使用正则化
- 不要和dropout同时使用
课后测验
1. 如果你有10,000,000个例子,你会如何划分训练/开发/测试集?
训练集占98% , 开发集占1% , 测试集占1% 。
2. 开发和测试集应该:
来自同一分布。
3. 如果你的神经网络模型似乎有很高的方差,下列哪个尝试是可能解决问题的?
添加正则化, 获取更多的训练数据 。
4. 你在一家超市的自动结帐亭工作,正在为苹果,香蕉和橘子制作分类器。 假设您的分类器在训练集上有0.5%的错误,以及开发集上有7%的错误。 以下哪项尝试是有希望改善你的分类器的分类效果的?
增加正则化参数lambda, 获取更多的训练数据 。
5. 什么是权重衰减?
正则化技术(例如L2正则化)导致梯度下降在每次迭代时权重收缩。
6.当你增加正则化超参数lambda时会发生什么?
权重会变得更小(接近0)
7. 在测试时候使用dropout时
不要随机消除节点,也不要在训练中使用的计算中保留1 / keep_prob因子。
8. 将参数keep_prob从(比如说)0.5增加到0.6可能会导致以下情况
正则化效应被减弱、使神经网络在结束时会在训练集上表现好一些。
9. 以下哪些技术可用于减少方差(减少过拟合):
Dropout、 L2 正则化 、 扩充数据集 。
10.为什么我们要归一化输入x?
它使成本函数更快地进行优化。
编程作业
这周的编程作业,我们需要做初始化、正则化以及梯度校验的代码。
首先我们导包
import numpy as np
import matplotlib.pyplot as plt
import sklearn
import sklearn.datasets
from course_2_week_1 import init_utils # 第一部分,初始化
from course_2_week_1 import reg_utils # 第二部分,正则化
from course_2_week_1 import gc_utils # 第三部分,梯度校验
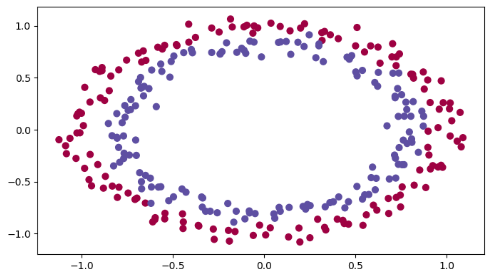
我们初始化一下数据,然后打印出来看一下数据效果。
train_X, train_Y, test_X, test_Y = init_utils.load_dataset(is_plot=True)
plt.show()
我们在这里尝试三种参数初始化方法,全部初始化为0、随机初始化与抑梯度异常初始化。
在这之前,我们先把模型搭建好(方法以后再说,解释性语言就是好啊x),然后使用不同的参数初始化方法进行对比(其他的前向反向传播等方法均在工具类中实现好了)。
),然后使用不同的参数初始化方法进行对比(其他的前向反向传播等方法均在工具类中实现好了)。
def model(X, Y, learning_rate=0.01, num_iteration=15000, print_cost=True, initialization="he", is_polt=True):
"""
神经网络模型
:param X:
:param Y:
:param learning_rate:
:param num_iteration:
:param print_cost:
:param initialization:
:param is_polt:
:return:
"""
grads = {}
costs = []
# 训练集个数
m = X.shape[1]
# 三层神经网络的结构
layers_dims = [X.shape[0], 10, 5, 1]
if initialization == 'zeros':
parameters = initialize_parameters_zeros(layers_dims)
elif initialization == 'random':
parameters = initialize_parameters_random(layers_dims)
elif initialization == "he":
parameters = initialize_parameters_he(layers_dims)
else:
print("错误的初始化参数!程序退出")
exit
# 开始学习
for i in range(num_iteration):
a3, cache = init_utils.forward_propagation(X, parameters)
cost = init_utils.compute_loss(a3, Y)
grads = init_utils.backward_propagation(X, Y, cache)
parameters = init_utils.update_parameters(parameters, grads, learning_rate)
if i % 1000 == 0:
costs.append(cost)
if print_cost:
print("第" + str(i) + "次迭代,成本值为:" + str(cost))
# 学习完毕,绘制成本曲线
if is_polt:
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
# 返回学习完毕后的参数
return parameters
首先我们尝试使用初始化0:
def initialize_parameters_zeros(layers_dims):
"""
模型的参数全部初始化为0
:param layers_dims:
:return:
"""
parameters = {}
# 网络层数
L = len(layers_dims)
for i in range(1, L):
parameters['W' + str(i)] = np.zeros((layers_dims[i], layers_dims[i - 1]))
parameters['b' + str(i)] = np.zeros((layers_dims[i], 1))
return parameters
然后我们运行模型
parameters = model(train_X, train_Y, initialization="zero", is_polt=True)
print("训练集:")
predictions_train = init_utils.predict(train_X, train_Y, parameters)
print("测试集:")
predictions_test = init_utils.predict(test_X, test_Y, parameters)
输出如下:
第0次迭代,成本值为:0.6931471805599453
第1000次迭代,成本值为:0.6931471805599453
第2000次迭代,成本值为:0.6931471805599453
第3000次迭代,成本值为:0.6931471805599453
第4000次迭代,成本值为:0.6931471805599453
第5000次迭代,成本值为:0.6931471805599453
第6000次迭代,成本值为:0.6931471805599453
第7000次迭代,成本值为:0.6931471805599453
第8000次迭代,成本值为:0.6931471805599453
第9000次迭代,成本值为:0.6931471805599453
第10000次迭代,成本值为:0.6931471805599455
第11000次迭代,成本值为:0.6931471805599453
第12000次迭代,成本值为:0.6931471805599453
训练集:
Accuracy: 0.5
测试集:
Accuracy: 0.5可以看到随着迭代次数的增加,代价没有任何变化。
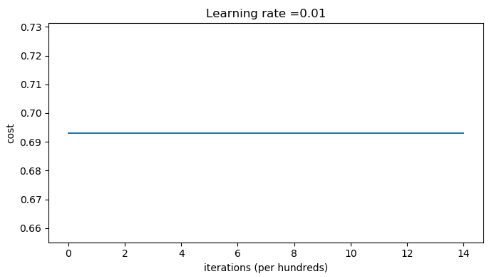
就像之前说的,当参数初始化为0的时候,神经网络就退化成逻辑回归了。
然后是使用随机初始化:
def initialize_parameters_random(layers_dims):
"""
模型随机初始化参数
:param layers_dims:
:return:
"""
np.random.seed(3)
parameters = {}
L = len(layers_dims)
for i in range(1, L):
parameters['W' + str(i)] = np.random.randn(layers_dims[i], layers_dims[i - 1]) * 10
parameters['b' + str(i)] = np.zeros((layers_dims[i], 1))
return parameters
然后调用输出并绘制决策边界。
parameters = model(train_X, train_Y, initialization="random", is_polt=True)
print("训练集:")
predictions_train = init_utils.predict(train_X, train_Y, parameters)
print("测试集:")
predictions_test = init_utils.predict(test_X, test_Y, parameters)
plt.title("Model with large random initialization")
axes = plt.gca()
axes.set_xlim([-1.5, 1.5])
axes.set_ylim([-1.5, 1.5])
init_utils.plot_decision_boundary(lambda x: init_utils.predict_dec(parameters, x.T), train_X, train_Y)
第0次迭代,成本值为:inf
第1000次迭代,成本值为:0.6250982793959966
第2000次迭代,成本值为:0.5981216596703697
第3000次迭代,成本值为:0.5638417572298645
第4000次迭代,成本值为:0.5501703049199763
第5000次迭代,成本值为:0.5444632909664456
第6000次迭代,成本值为:0.5374513807000807
第7000次迭代,成本值为:0.4764042074074983
第8000次迭代,成本值为:0.39781492295092263
第9000次迭代,成本值为:0.3934764028765484
第10000次迭代,成本值为:0.3920295461882659
第11000次迭代,成本值为:0.38924598135108
第12000次迭代,成本值为:0.3861547485712325
第13000次迭代,成本值为:0.384984728909703
第14000次迭代,成本值为:0.3827828308349524
训练集:
Accuracy: 0.83
测试集:
Accuracy: 0.86代价曲线:
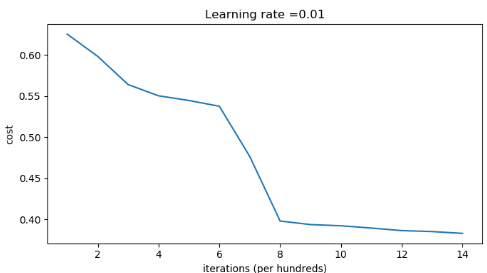
决策边界:

初始化的时候乘了个10,如果我们将这个10去掉变成1,那么准确率就会达到96%。说明这个超参也能影响准确度,这与这个数变成多少比较好,下面会说。
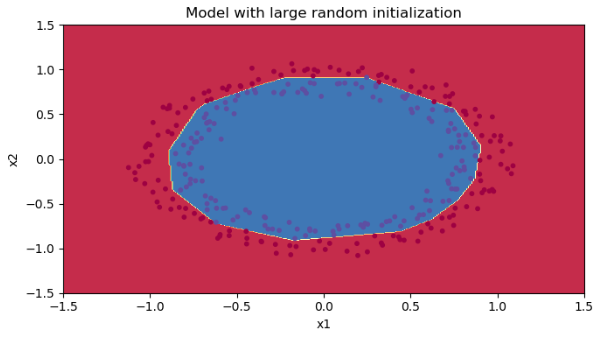
然后是抑梯度异常初始化:
def initialize_parameters_he(layers_dims):
"""
抑梯度异常初始化
:param layers_dims:
:return:
"""
np.random.seed(3)
parameters = {}
L = len(layers_dims)
for i in range(1, L):
print(np.sqrt(2 / layers_dims[i - 1]))
parameters['W' + str(i)] = np.random.randn(layers_dims[i], layers_dims[i - 1]) * np.sqrt(2 / layers_dims[i - 1])
parameters['b' + str(i)] = np.zeros((layers_dims[i], 1))
return parameters
然后输出结果和绘制决策边界:
parameters = model(train_X, train_Y, initialization="he", is_polt=True)
print("训练集:")
predictions_train = init_utils.predict(train_X, train_Y, parameters)
print("测试集:")
predictions_test = init_utils.predict(test_X, test_Y, parameters)
plt.title("Model with large random initialization")
axes = plt.gca()
axes.set_xlim([-1.5, 1.5])
axes.set_ylim([-1.5, 1.5])
init_utils.plot_decision_boundary(lambda x: init_utils.predict_dec(parameters, x.T), train_X, train_Y)
第0次迭代,成本值为:0.8830537463419761
第1000次迭代,成本值为:0.6879825919728063
第2000次迭代,成本值为:0.6751286264523371
第3000次迭代,成本值为:0.6526117768893807
第4000次迭代,成本值为:0.6082958970572937
第5000次迭代,成本值为:0.5304944491717495
第6000次迭代,成本值为:0.4138645817071793
第7000次迭代,成本值为:0.3117803464844441
第8000次迭代,成本值为:0.23696215330322556
第9000次迭代,成本值为:0.18597287209206828
第10000次迭代,成本值为:0.15015556280371808
第11000次迭代,成本值为:0.12325079292273548
第12000次迭代,成本值为:0.09917746546525937
第13000次迭代,成本值为:0.08457055954024274
第14000次迭代,成本值为:0.07357895962677366
训练集:
Accuracy: 0.9933333333333333
测试集:
Accuracy: 0.96代价变化曲线:
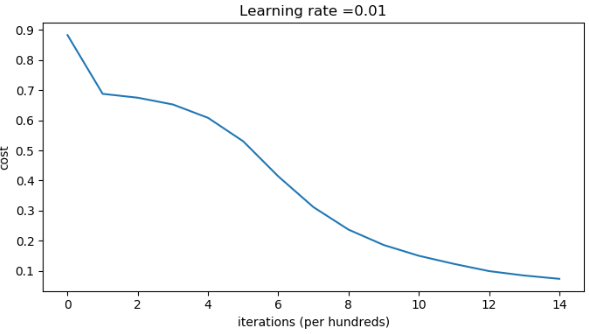
决策边界
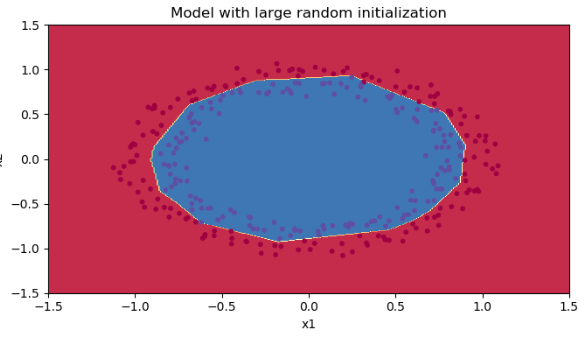
我们发现准确度很高,并且决策边界和上面超参为1的时候很像,我们输出一下这个超参看看。
1.0
0.4472135954999579
0.6324555320336759发现基本也在1附近。
处理完参数初始化,我们接下来学习正则化的相关知识。
第0次迭代,成本值为:0.6557412523481002
第5000次迭代,成本值为:0.17620471758400447
第10000次迭代,成本值为:0.1632998752572419
第15000次迭代,成本值为:0.14796400922574113
第20000次迭代,成本值为:0.13851642423239133
第25000次迭代,成本值为:0.13285370211487862
训练集:
Accuracy: 0.9478672985781991
测试集:
Accuracy: 0.915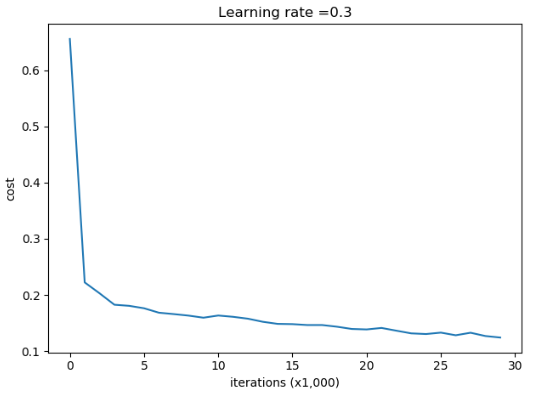
然后是正则化:
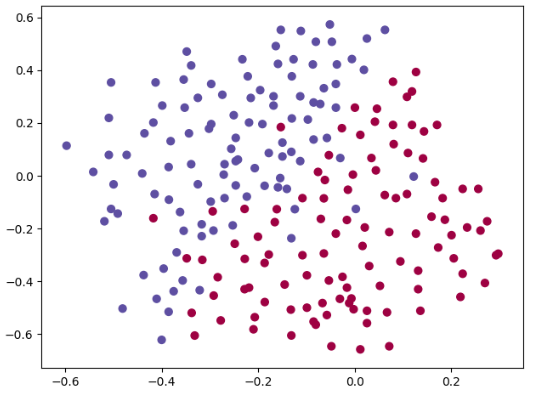
首先我们导入数据
train_X, train_Y, test_X, test_Y = reg_utils.load_2D_dataset()
plt.show()
还是和之前一样,我们先写模型,对于方法以后实现:
def model(X, Y, learning_rate=0.3, num_iterations=30000, print_cost=True, is_plot=True, lambd=0.0, keep_prob=1.0):
"""
模型主体
:param X:
:param Y:
:param learning_rate:
:param num_iterations:
:param print_cost:
:param is_plot:
:param lambd:
:param keep_prob:
:return:
"""
grads = {}
costs = []
m = X.shape[1]
layers_dims = [X.shape[0], 20, 3, 1]
# 这个初始化后台也是抑梯度异常初始化
parameters = reg_utils.initialize_parameters(layers_dims)
for i in range(num_iterations):
# dropout
if keep_prob == 1:
a3, cache = reg_utils.forward_propagation(X, parameters)
elif keep_prob < 1:
a3, cache = forward_propagation_with_dropout(X, parameters, keep_prob)
# 正则化
if lambd == 0:
# 不使用L2正则化
cost = reg_utils.compute_cost(a3, Y)
else:
# 使用L2正则化
cost = compute_cost_with_regularization(a3, Y, parameters, lambd)
# 反向传播
# 可以同时使用L2正则化和随机删除节点,但是本次实验不同时使用。
assert (lambd == 0 or keep_prob == 1)
# 两个参数的使用情况
if (lambd == 0 and keep_prob == 1):
# 不使用L2正则化和不使用随机删除节点
grads = reg_utils.backward_propagation(X, Y, cache)
elif lambd != 0:
# 使用L2正则化,不使用随机删除节点
grads = backward_propagation_with_regularization(X, Y, cache, lambd)
elif keep_prob < 1:
# 使用随机删除节点,不使用L2正则化
grads = backward_propagation_with_dropout(X, Y, cache, keep_prob)
parameters = reg_utils.update_parameters(parameters, grads, learning_rate)
if i % 1000 == 0:
costs.append(cost)
if (print_cost and i % 5000 == 0):
print("第" + str(i) + "次迭代,成本值为:" + str(cost))
if is_plot:
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (x1,000)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parameters
首先是正则化的前向传播:
def compute_cost_with_regularization(A3, Y, parameters, lambd):
"""
正则化前向传播
:return:
"""
m = Y.shape[1]
W1 = parameters['W1']
W2 = parameters['W2']
W3 = parameters['W3']
cost = reg_utils.compute_cost(A3, Y)
L2_regularization_cost = lambd * (np.sum(np.square(W1)) + np.sum(np.square(W2)) + np.sum(np.square(W3))) / (2 * m)
cost = cost + L2_regularization_cost
return cost
然后是正则化的反向传播:
def backward_propagation_with_regularization(X, Y, cache, lambd):
"""
因为代价函数的改变,反向传播的过程也要改变
:param X:
:param Y:
:param cache:
:param lambd:
:return:
"""
m = X.shape[1]
(Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = (1 / m) * np.dot(dZ3, A2.T) + ((lambd * W3) / m)
db3 = (1 / m) * np.sum(dZ3, axis=1, keepdims=True)
dA2 = np.dot(W3.T, dZ3)
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = (1 / m) * np.dot(dZ2, A1.T) + ((lambd * W2) / m)
db2 = (1 / m) * np.sum(dZ2, axis=1, keepdims=True)
dA1 = np.dot(W2.T, dZ2)
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = (1 / m) * np.dot(dZ1, X.T) + ((lambd * W1) / m)
db1 = (1 / m) * np.sum(dZ1, axis=1, keepdims=True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3, "dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
然后我们调用训练
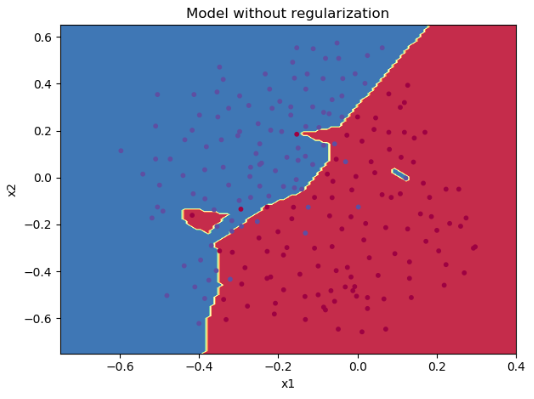
parameters = model(train_X, train_Y, is_plot=True, lambd=0.7)
print("训练集:")
predictions_train = reg_utils.predict(train_X, train_Y, parameters)
print("测试集:")
predictions_test = reg_utils.predict(test_X, test_Y, parameters)
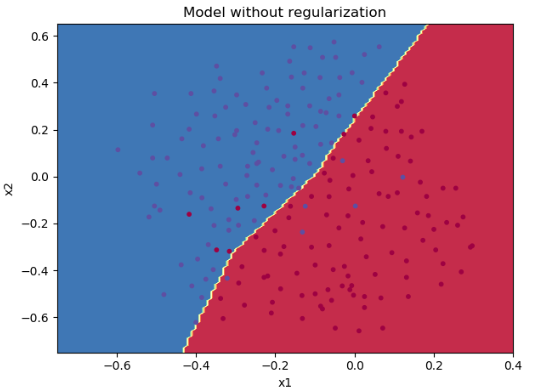
plt.title("Model without regularization")
axes = plt.gca()
axes.set_xlim([-0.75, 0.40])
axes.set_ylim([-0.75, 0.65])
reg_utils.plot_decision_boundary(lambda x: reg_utils.predict_dec(parameters, x.T), train_X, train_Y)
我们可以看到输出如下:
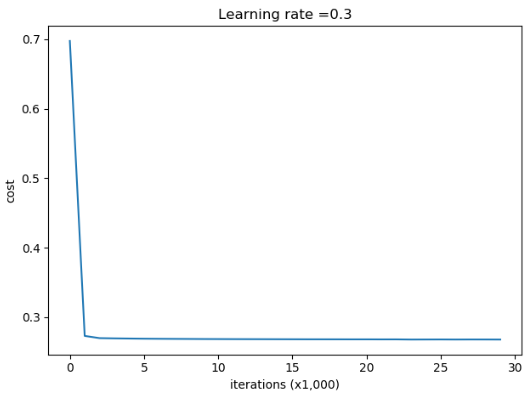
第0次迭代,成本值为:0.6974484493131264
第5000次迭代,成本值为:0.2690430474349705
第10000次迭代,成本值为:0.2684918873282239
第15000次迭代,成本值为:0.2682199033729048
第20000次迭代,成本值为:0.2680916337127301
第25000次迭代,成本值为:0.26794285663887024
训练集:
Accuracy: 0.9383886255924171
测试集:
Accuracy: 0.93代价变化曲线:
决策边界:
然后就是dropout的前向和反向传播过程:
def forward_propagation_with_dropout(X, parameters, keep_prob=0.5):
"""
随机舍弃结点的前向传播
:param X:
:param parameters:
:param keep_prob:
:return:
"""
np.random.seed(1)
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
W3 = parameters["W3"]
b3 = parameters["b3"]
Z1 = np.dot(W1, X) + b1
A1 = reg_utils.relu(Z1)
# 随机初始化一个0~1的矩阵,然后根据初始化的值重新计算A1,最后缩小一点A
D1 = np.random.rand(A1.shape[0], A1.shape[1])
D1 = D1 < keep_prob
A1 = A1 * D1
A1 = A1 / keep_prob
Z2 = np.dot(W2, A1) + b2
A2 = reg_utils.relu(Z2)
D2 = np.random.rand(A2.shape[0], A2.shape[1])
D2 = D2 < keep_prob
A2 = A2 * D2
A2 = A2 / keep_prob
Z3 = np.dot(W3, A2) + b3
A3 = reg_utils.sigmoid(Z3)
cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3)
return A3, cache
def backward_propagation_with_dropout(X, Y, cache, keep_prob):
"""
随机舍弃结点的反向传播
:param X:
:param Y:
:param cache:
:param keep_prob:
:return:
"""
m = X.shape[1]
(Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = (1 / m) * np.dot(dZ3, A2.T)
db3 = 1. / m * np.sum(dZ3, axis=1, keepdims=True)
dA2 = np.dot(W3.T, dZ3)
# 根据前向随机舍弃的结点重新计算A,并缩放A
dA2 = dA2 * D2
dA2 = dA2 / keep_prob
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1. / m * np.dot(dZ2, A1.T)
db2 = 1. / m * np.sum(dZ2, axis=1, keepdims=True)
dA1 = np.dot(W2.T, dZ2)
dA1 = dA1 * D1
dA1 = dA1 / keep_prob
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1. / m * np.dot(dZ1, X.T)
db1 = 1. / m * np.sum(dZ1, axis=1, keepdims=True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3, "dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
输出如下:
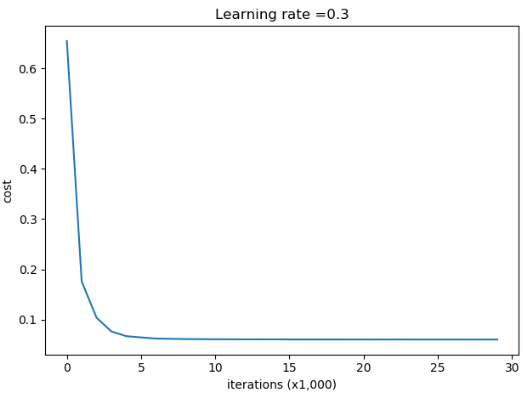
第0次迭代,成本值为:0.6543912405149825
第5000次迭代,成本值为:0.06466905008519824
第10000次迭代,成本值为:0.061016986574905605
第15000次迭代,成本值为:0.060664572161287754
第20000次迭代,成本值为:0.060582435798513114
第25000次迭代,成本值为:0.06050179002362491
训练集:
Accuracy: 0.9289099526066351
测试集:
Accuracy: 0.95代价变化曲线
决策边界:

我们可以看到,虽然整体的训练集准确率降低了,但是测试集准确率却上升了,说明正则化一定程度上消除了过拟合。
完整代码:
# -*- coding:utf-8 -*-
"""
┏┛ ┻━━━━━┛ ┻┓
┃ ┃
┃ ━ ┃
┃ ┳┛ ┗┳ ┃
┃ ┃
┃ ┻ ┃
┃ ┃
┗━┓ ┏━━━┛
┃ ┃ 神兽保佑
┃ ┃ 代码无BUG!
┃ ┗━━━━━━━━━┓
┃ ┣┓
┃ ┏┛
┗━┓ ┓ ┏━━━┳ ┓ ┏━┛
┃ ┫ ┫ ┃ ┫ ┫
┗━┻━┛ ┗━┻━┛
"""
import numpy as np
import matplotlib.pyplot as plt
import sklearn
import sklearn.datasets
from course_2_week_1 import init_utils # 第一部分,初始化
from course_2_week_1 import reg_utils # 第二部分,正则化
from course_2_week_1 import gc_utils # 第三部分,梯度校验
# plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
# plt.rcParams['image.interpolation'] = 'nearest'
# plt.rcParams['image.cmap'] = 'gray'
# 初始化数据
# train_X, train_Y, test_X, test_Y = init_utils.load_dataset(is_plot=True)
# plt.show()
def initialize_parameters_zeros(layers_dims):
"""
模型的参数全部初始化为0
:param layers_dims:
:return:
"""
parameters = {}
# 网络层数
L = len(layers_dims)
for i in range(1, L):
parameters['W' + str(i)] = np.zeros((layers_dims[i], layers_dims[i - 1]))
parameters['b' + str(i)] = np.zeros((layers_dims[i], 1))
return parameters
def initialize_parameters_random(layers_dims):
"""
模型随机初始化参数
:param layers_dims:
:return:
"""
np.random.seed(3)
parameters = {}
L = len(layers_dims)
for i in range(1, L):
parameters['W' + str(i)] = np.random.randn(layers_dims[i], layers_dims[i - 1]) * 10
parameters['b' + str(i)] = np.zeros((layers_dims[i], 1))
return parameters
def initialize_parameters_he(layers_dims):
"""
抑梯度异常初始化
:param layers_dims:
:return:
"""
np.random.seed(3)
parameters = {}
L = len(layers_dims)
for i in range(1, L):
print(np.sqrt(2 / layers_dims[i - 1]))
parameters['W' + str(i)] = np.random.randn(layers_dims[i], layers_dims[i - 1]) * np.sqrt(2 / layers_dims[i - 1])
parameters['b' + str(i)] = np.zeros((layers_dims[i], 1))
return parameters
def model(X, Y, learning_rate=0.01, num_iteration=15000, print_cost=True, initialization="he", is_polt=True):
"""
神经网络模型
:param X:
:param Y:
:param learning_rate:
:param num_iteration:
:param print_cost:
:param initialization:
:param is_polt:
:return:
"""
grads = {}
costs = []
# 训练集个数
m = X.shape[1]
# 三层神经网络的结构
layers_dims = [X.shape[0], 10, 5, 1]
if initialization == 'zeros':
parameters = initialize_parameters_zeros(layers_dims)
elif initialization == 'random':
parameters = initialize_parameters_random(layers_dims)
elif initialization == "he":
parameters = initialize_parameters_he(layers_dims)
else:
print("错误的初始化参数!程序退出")
exit
# 开始学习
for i in range(num_iteration):
a3, cache = init_utils.forward_propagation(X, parameters)
cost = init_utils.compute_loss(a3, Y)
grads = init_utils.backward_propagation(X, Y, cache)
parameters = init_utils.update_parameters(parameters, grads, learning_rate)
if i % 1000 == 0:
costs.append(cost)
if print_cost:
print("第" + str(i) + "次迭代,成本值为:" + str(cost))
# 学习完毕,绘制成本曲线
if is_polt:
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (per hundreds)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
# 返回学习完毕后的参数
return parameters
# parameters = model(train_X, train_Y, initialization="he", is_polt=True)
# print("训练集:")
# predictions_train = init_utils.predict(train_X, train_Y, parameters)
# print("测试集:")
# predictions_test = init_utils.predict(test_X, test_Y, parameters)
#
# plt.title("Model with large random initialization")
# axes = plt.gca()
# axes.set_xlim([-1.5, 1.5])
# axes.set_ylim([-1.5, 1.5])
# init_utils.plot_decision_boundary(lambda x: init_utils.predict_dec(parameters, x.T), train_X, train_Y)
# 正则化
# 首先是读取数据
# train_X, train_Y, test_X, test_Y = reg_utils.load_2D_dataset()
# plt.show()
def compute_cost_with_regularization(A3, Y, parameters, lambd):
"""
正则化前向传播
:return:
"""
m = Y.shape[1]
W1 = parameters['W1']
W2 = parameters['W2']
W3 = parameters['W3']
cost = reg_utils.compute_cost(A3, Y)
L2_regularization_cost = lambd * (np.sum(np.square(W1)) + np.sum(np.square(W2)) + np.sum(np.square(W3))) / (2 * m)
cost = cost + L2_regularization_cost
return cost
def backward_propagation_with_regularization(X, Y, cache, lambd):
"""
因为代价函数的改变,反向传播的过程也要改变
:param X:
:param Y:
:param cache:
:param lambd:
:return:
"""
m = X.shape[1]
(Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = (1 / m) * np.dot(dZ3, A2.T) + ((lambd * W3) / m)
db3 = (1 / m) * np.sum(dZ3, axis=1, keepdims=True)
dA2 = np.dot(W3.T, dZ3)
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = (1 / m) * np.dot(dZ2, A1.T) + ((lambd * W2) / m)
db2 = (1 / m) * np.sum(dZ2, axis=1, keepdims=True)
dA1 = np.dot(W2.T, dZ2)
dZ1 = np.multiply(dA1, np.int 64(A1 > 0))
dW1 = (1 / m) * np.dot(dZ1, X.T) + ((lambd * W1) / m)
db1 = (1 / m) * np.sum(dZ1, axis=1, keepdims=True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3, "dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
def forward_propagation_with_dropout(X, parameters, keep_prob=0.5):
"""
随机舍弃结点的前向传播
:param X:
:param parameters:
:param keep_prob:
:return:
"""
np.random.seed(1)
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
W3 = parameters["W3"]
b3 = parameters["b3"]
Z1 = np.dot(W1, X) + b1
A1 = reg_utils.relu(Z1)
# 随机初始化一个0~1的矩阵,然后根据初始化的值重新计算A1,最后缩小一点A
D1 = np.random.rand(A1.shape[0], A1.shape[1])
D1 = D1 < keep_prob
A1 = A1 * D1
A1 = A1 / keep_prob
Z2 = np.dot(W2, A1) + b2
A2 = reg_utils.relu(Z2)
D2 = np.random.rand(A2.shape[0], A2.shape[1])
D2 = D2 < keep_prob
A2 = A2 * D2
A2 = A2 / keep_prob
Z3 = np.dot(W3, A2) + b3
A3 = reg_utils.sigmoid(Z3)
cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3)
return A3, cache
def backward_propagation_with_dropout(X, Y, cache, keep_prob):
"""
随机舍弃结点的反向传播
:param X:
:param Y:
:param cache:
:param keep_prob:
:return:
"""
m = X.shape[1]
(Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = (1 / m) * np.dot(dZ3, A2.T)
db3 = 1. / m * np.sum(dZ3, axis=1, keepdims=True)
dA2 = np.dot(W3.T, dZ3)
# 根据前向随机舍弃的结点重新计算A,并缩放A
dA2 = dA2 * D2
dA2 = dA2 / keep_prob
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1. / m * np.dot(dZ2, A1.T)
db2 = 1. / m * np.sum(dZ2, axis=1, keepdims=True)
dA1 = np.dot(W2.T, dZ2)
dA1 = dA1 * D1
dA1 = dA1 / keep_prob
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1. / m * np.dot(dZ1, X.T)
db1 = 1. / m * np.sum(dZ1, axis=1, keepdims=True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3, "dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
def model(X, Y, learning_rate=0.3, num_iterations=30000, print_cost=True, is_plot=True, lambd=0.0, keep_prob=1.0):
"""
模型主体
:param X:
:param Y:
:param learning_rate:
:param num_iterations:
:param print_cost:
:param is_plot:
:param lambd:
:param keep_prob:
:return:
"""
grads = {}
costs = []
m = X.shape[1]
layers_dims = [X.shape[0], 20, 3, 1]
# 这个初始化后台也是抑梯度异常初始化
parameters = reg_utils.initialize_parameters(layers_dims)
for i in range(num_iterations):
# dropout
if keep_prob == 1:
a3, cache = reg_utils.forward_propagation(X, parameters)
elif keep_prob < 1:
a3, cache = forward_propagation_with_dropout(X, parameters, keep_prob)
# 正则化
if lambd == 0:
# 不使用L2正则化
cost = reg_utils.compute_cost(a3, Y)
else:
# 使用L2正则化
cost = compute_cost_with_regularization(a3, Y, parameters, lambd)
# 反向传播
# 可以同时使用L2正则化和随机删除节点,但是本次实验不同时使用。
assert (lambd == 0 or keep_prob == 1)
# 两个参数的使用情况
if (lambd == 0 and keep_prob == 1):
# 不使用L2正则化和不使用随机删除节点
grads = reg_utils.backward_propagation(X, Y, cache)
elif lambd != 0:
# 使用L2正则化,不使用随机删除节点
grads = backward_propagation_with_regularization(X, Y, cache, lambd)
elif keep_prob < 1:
# 使用随机删除节点,不使用L2正则化
grads = backward_propagation_with_dropout(X, Y, cache, keep_prob)
parameters = reg_utils.update_parameters(parameters, grads, learning_rate)
if i % 1000 == 0:
costs.append(cost)
if (print_cost and i % 5000 == 0):
print("第" + str(i) + "次迭代,成本值为:" + str(cost))
if is_plot:
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (x1,000)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
return parameters
# parameters = model(train_X, train_Y, is_plot=True)
# parameters = model(train_X, train_Y, is_plot=True, lambd=0.7)
# # parameters = model(train_X, train_Y, is_plot=True, keep_prob=0.86)
# print("训练集:")
# predictions_train = reg_utils.predict(train_X, train_Y, parameters)
# print("测试集:")
# predictions_test = reg_utils.predict(test_X, test_Y, parameters)
#
# plt.title("Model without regularization")
# axes = plt.gca()
# axes.set_xlim([-0.75, 0.40])
# axes.set_ylim([-0.75, 0.65])
# reg_utils.plot_decision_boundary(lambda x: reg_utils.predict_dec(parameters, x.T), train_X, train_Y)
# 梯度校验
# 现在假设定义一个一维的线性函数
def forward_propagation(x, theta):
"""
一维线性函数的前向传播
:param x:
:param theta:
:return:
"""
J = np.dot(theta, x)
return J
def backward_propagation(x, theta):
"""
一阶线性的反向传播
:param x:
:param theta:
:return:
"""
dtheta = x
return dtheta
def gradient_check(x, theta, epsilon=1e-7):
"""
验证梯度校验
:param x:
:param theta:
:param epsilon:
:return:
"""
# 使用公式(3)的左侧计算gradapprox。
thetaplus = theta + epsilon # Step 1
thetaminus = theta - epsilon # Step 2
J_plus = forward_propagation(x, thetaplus) # Step 3
J_minus = forward_propagation(x, thetaminus) # Step 4
gradapprox = (J_plus - J_minus) / (2 * epsilon) # Step 5
# 检查gradapprox是否足够接近backward_propagation()的输出
grad = backward_propagation(x, theta)
# 求二范数
numerator = np.linalg.norm(grad - gradapprox) # Step 1'
denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox) # Step 2'
difference = numerator / denominator # Step 3'
if difference < 1e-7:
print("梯度检查:梯度正常!")
else:
print("梯度检查:梯度超出阈值!")
return difference
# print("-----------------测试gradient_check-----------------")
# x, theta = 2, 4
# difference = gradient_check(x, theta)
# print("difference = " + str(difference))
def forward_propagation_n(X, Y, parameters):
"""
前向传播并计算代价
:param X:
:param Y:
:param parameters:
:return:
"""
m = X.shape[1]
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
W3 = parameters["W3"]
b3 = parameters["b3"]
Z1 = np.dot(W1, X) + b1
A1 = gc_utils.relu(Z1)
Z2 = np.dot(W2, A1) + b2
A2 = gc_utils.relu(Z2)
Z3 = np.dot(W3, A2) + b3
A3 = gc_utils.sigmoid(Z3)
# 计算成本
logprobs = np.multiply(-np.log(A3), Y) + np.multiply(-np.log(1 - A3), 1 - Y)
cost = (1 / m) * np.sum(logprobs)
cache = (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3)
return cost, cache
def backward_propagation_n(X, Y, cache):
"""
反向传播
:param X:
:param Y:
:param cache:
:return:
"""
m = X.shape[1]
(Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = 1. / m * np.dot(dZ3, A2.T)
db3 = 1. / m * np.sum(dZ3, axis=1, keepdims=True)
dA2 = np.dot(W3.T, dZ3)
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1. / m * np.dot(dZ2, A1.T)
db2 = 1. / m * np.sum(dZ2, axis=1, keepdims=True)
dA1 = np.dot(W2.T, dZ2)
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1. / m * np.dot(dZ1, X.T)
db1 = 1. / m * np.sum(dZ1, axis=1, keepdims=True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,
"dA2": dA2, "dZ2": dZ2, "dW2": dW2, "db2": db2,
"dA1": dA1, "dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
def gradient_check_n(parameters, gradients, X, Y, epsilon=1e-7):
"""
梯度校验
:param parameters:
:param gradients:
:param X:
:param Y:
:param epsilon:
:return:
"""
# 初始化参数
parameters_values, keys = gc_utils.dictionary_to_vector(parameters) # keys用不到
grad = gc_utils.gradients_to_vector(gradients)
num_parameters = parameters_values.shape[0]
J_plus = np.zeros((num_parameters, 1))
J_minus = np.zeros((num_parameters, 1))
gradapprox = np.zeros((num_parameters, 1))
# 计算gradapprox
for i in range(num_parameters):
# 计算J_plus [i]。输入:“parameters_values,epsilon”。输出=“J_plus [i]”
thetaplus = np.copy(parameters_values) # Step 1
thetaplus[i][0] = thetaplus[i][0] + epsilon # Step 2
J_plus[i], cache = forward_propagation_n(X, Y, gc_utils.vector_to_dictionary(thetaplus)) # Step 3 ,cache用不到
# 计算J_minus [i]。输入:“parameters_values,epsilon”。输出=“J_minus [i]”。
thetaminus = np.copy(parameters_values) # Step 1
thetaminus[i][0] = thetaminus[i][0] - epsilon # Step 2
J_minus[i], cache = forward_propagation_n(X, Y, gc_utils.vector_to_dictionary(thetaminus)) # Step 3 ,cache用不到
# 计算gradapprox[i]
gradapprox[i] = (J_plus[i] - J_minus[i]) / (2 * epsilon)
# 通过计算差异比较gradapprox和后向传播梯度。
numerator = np.linalg.norm(grad - gradapprox) # Step 1'
denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox) # Step 2'
difference = numerator / denominator # Step 3'
if difference < 1e-7:
print("梯度检查:梯度正常!")
else:
print("梯度检查:梯度超出阈值!")
return difference
0 条评论