吴恩达深度学习第四课 第一周 卷积神经网络

1.计算机视觉
深度学习与计算机视觉可以帮助汽车,查明周围的行人和汽车,并帮助汽车避开它们。还使得人脸识别技术变得更加效率和精准,你们即将能够体验到或早已体验过仅仅通过刷脸就能解锁手机或者门锁。当你解锁了手机,我猜手机上一定有很多分享图片的应用。在上面,你能看到美食,酒店或美丽风景的图片。有些公司在这些应用上使用了深度学习技术来向你展示最为生动美丽以及与你最为相关的图片。

我们现在已经可以做64*64大小的猫识别,算上RGB也就是64*64*3个数据,也就是12288个,那么如果我们要计算1000*1000大小的图片,就需要超级多的参数,大概300w个。
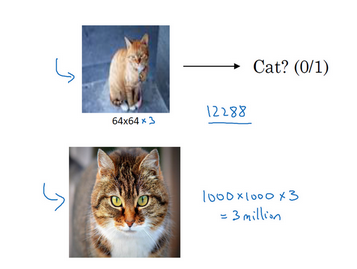
因此引入卷积神经网络来解决比较大的图片训练问题。
2.边缘检测算法
利用边缘监测算法我们可以检测出图片的横边和竖边
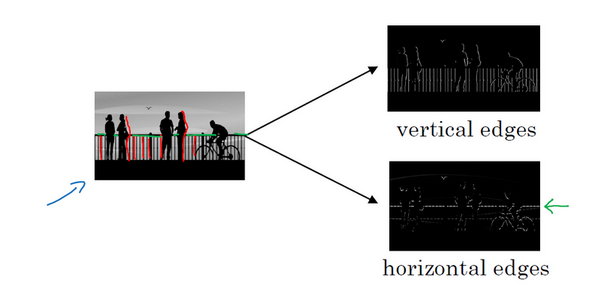
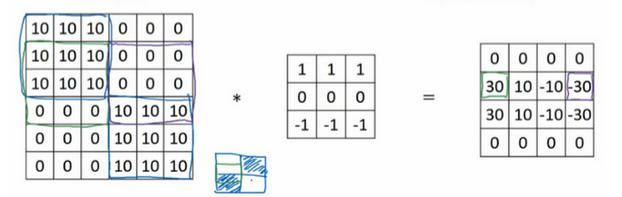
它的原理实际上是通过卷积操作,重新计算值:
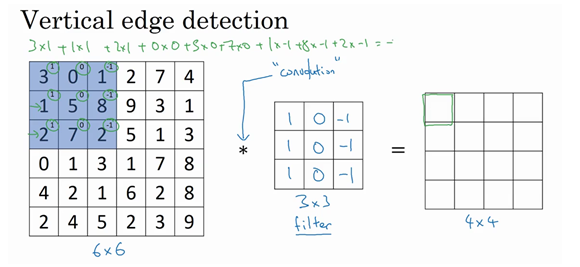
如图,对图片左上的3*3进行计算然后填入输出的最左上的位置,然后以此类推
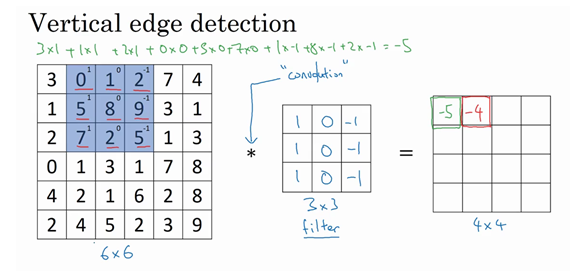
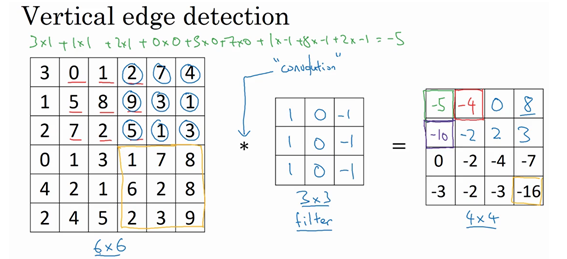
这个操作叫卷积操作,这里只是用‘*’来进行表示,在TensorFlow中我们可以使用tf.conv2d来进行这项操作。
他有什么效果呢?为什么能够进行边界划分呢?
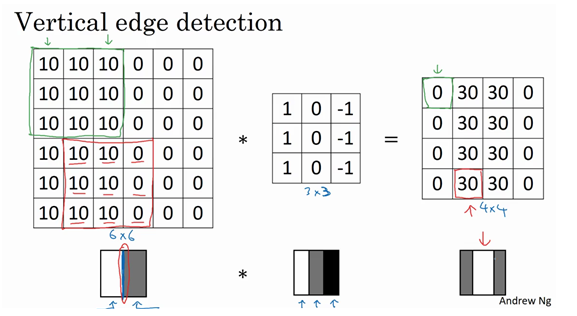
我们可以看到确实在边界上做出了区分,同时还可以有明暗或者暗明区分:
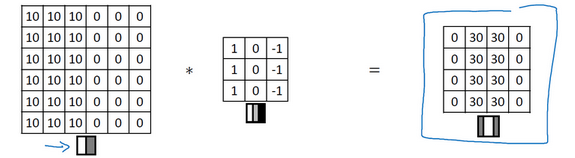
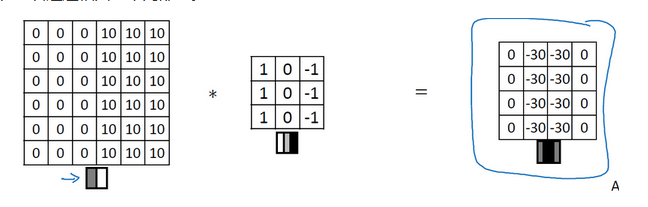
同理,如果我们使用横向的卷积矩阵,我们也可以获得横向的边界
而卷积矩阵中的参数我们也可以变(下图分别是 Sobel过滤器和Scharr过滤器 ):
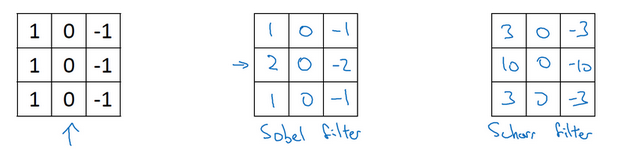
甚至可以把他们当做参数来使用:
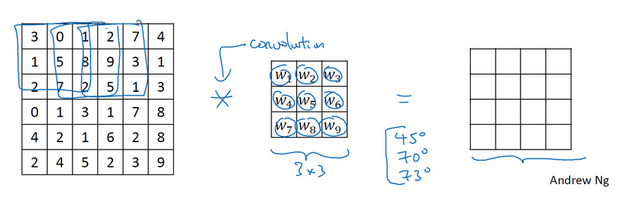
3.Padding
我们发现每经过卷积图片都变小了,为了避免这种情况,我们将原图片扩大,这样就不会变小了
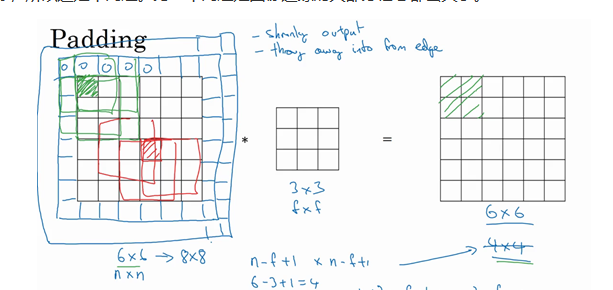
我们称没有使用padding的叫做Valid卷积(卷积后图片变小),使用Padding的称作Same卷积(卷积后图片不变小)。
4.卷积步长
这个也挺好解释,之前我们是一步一步移动,这时候卷积步长就为1.
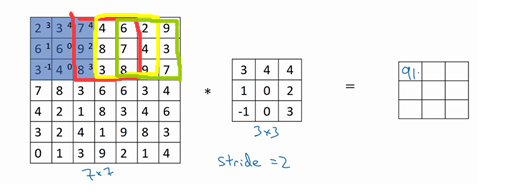
这是步长为2时的情况
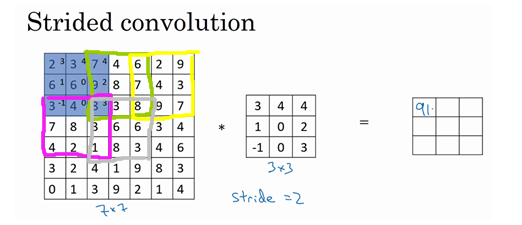
5.三维卷积
我们了解了卷积的操作,那么如何处理图片的RGB数据呢?就是使用三维卷积,也就是可以理解成进行三次卷积操作
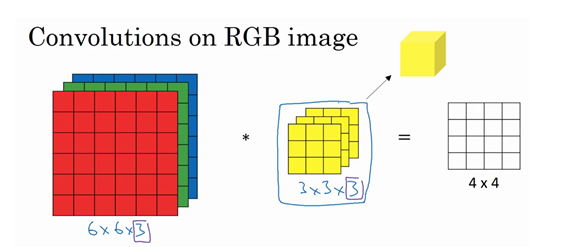
相当于只用正方体的块进行检查
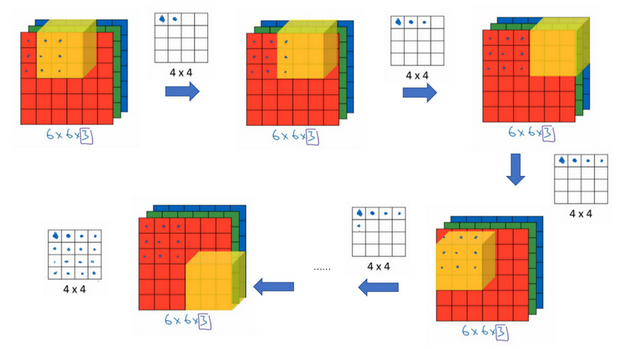
6.简单卷积网络示例
通过卷积网络,将一个图片变小,特征变大(相当于检测了20个特征)
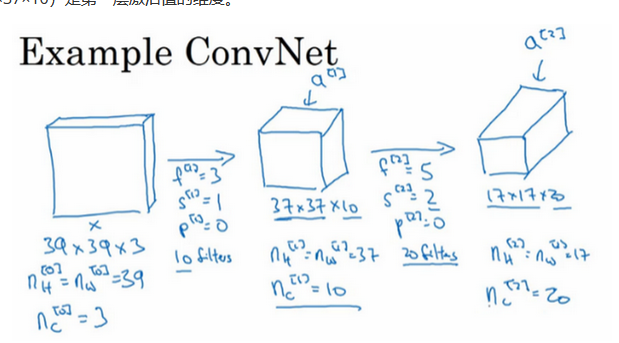
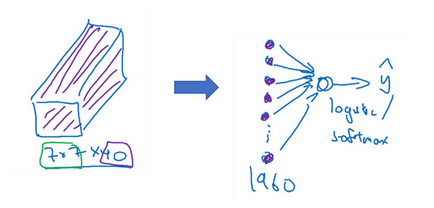
我们得到最后一个长方体之后,使用sigmoid或者softmax(这取决于是要进行二分类还是多分类)就可以得到结果。
7.池化层
最大池化
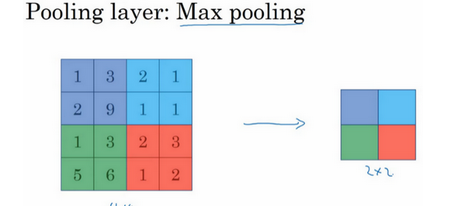
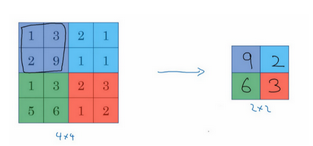
就是在一个大小内找最大值,用途呢可能就是防止图片太大一个特征的提取,因为没有参数,只是一个固定的步骤,所以他的超参就只是窗口大小和步数。
还有平均池化
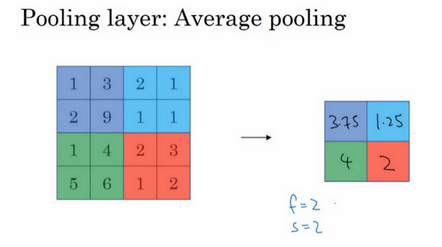
目前来说最大池化比平均池化更常用。
8.卷积神经网络示例
如下图,就是一个较为完整的卷积神经网络的结构:
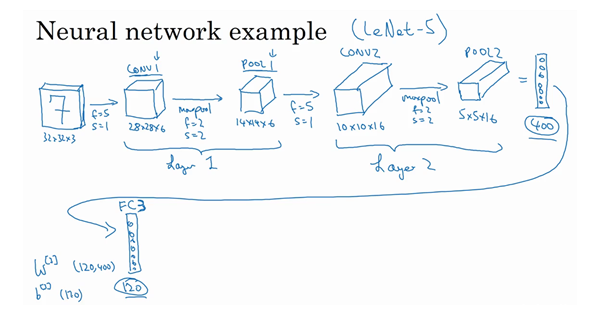
首先就是一个32*32的RGB图片,然后经过第一次卷积(因为池化没有参数,所以很多人认为卷积和池化属于一层),变成了10*10*16,相当于我们提取出来了16个特征,继续向下,经过第二层我们继续变成5*5*16,水平展开就是400个参数,然后使用全连接网络,继续向下训练,120个结点->->直到出来我们想要的结果
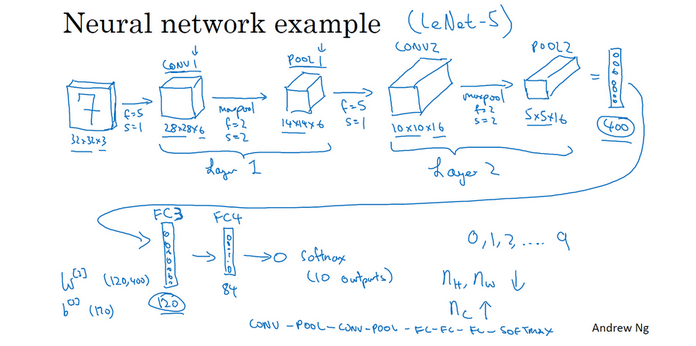
9.为什么使用卷积?
和全连接层相比,卷积的两个优势主要在参数共享和稀疏连接。
测验
1. 你认为把下面这个过滤器应用到灰度图像会怎么样?
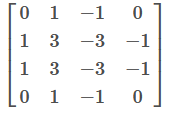
- 会检测45度边缘
- 会检测垂直边缘
- 会检测水平边缘
- 会检测图像对比度
2。
2. 假设你的输入是一个300×300的彩色(RGB)图像,而你没有使用卷积神经网络。 如果第一个隐藏层有100个神经元,每个神经元与输入层进行全连接,那么这个隐藏层有多少个参数(包括偏置参数)?
27,000,100 (300*300*3*100+100(偏置))
3. 假设你的输入是300×300彩色(RGB)图像,并且你使用卷积层和100个过滤器,每个过滤器都是5×5的大小,请问这个隐藏层有多少个参数(包括偏置参数)?
7600( (5*5*3+1)*00 )
4. 你有一个63x63x16的输入,并使用大小为7×7的32个过滤器进行卷积,使用步幅为2和无填充,请问输出是多少?
29*29*32 【(( 63+2*0-7 )/2)+1】0是padding
5. 你有一个15x15x8的输入,并使用“pad = 2”进行填充,填充后的尺寸是多少?
19*19*8
6. 你有一个63x63x16的输入,有32个过滤器进行卷积,每个过滤器的大小为7×7,步幅为1,你想要使用“same”的卷积方式,请问pad的值是多少?
3【(7-1)/2】
7. 你有一个32x32x16的输入,并使用步幅为2、过滤器大小为2的最大化池,请问输出是多少?
16*16*16
8. 因为池化层不具有参数,所以它们不影响反向传播的计算。
错误。
9. 在视频中,我们谈到了“参数共享”是使用卷积网络的好处。关于参数共享的下列哪个陈述是正确的?(检查所有选项。)
- 它减少了参数的总数,从而减少过拟合。
- 它允许在整个输入值的多个位置使用特征检测器。
- 它允许为一项任务学习的参数即使对于不同的任务也可以共享(迁移学习)。
- 它允许梯度下降将许多参数设置为零,从而使得连接稀疏。
2,4。
10. 在课堂上,我们讨论了“稀疏连接”是使用卷积层的好处。这是什么意思?
- 正则化导致梯度下降将许多参数设置为零。
- 每个过滤器都连接到上一层的每个通道。
- 下一层中的每个激活只依赖于前一层的少量激活。
- 卷积网络中的每一层只连接到另外两层。
3。
编程作业
这节课刚开始先简单介绍手写卷积网络相关知识,然后试图使用卷积网络进行上节课的手势识别。
首先手写卷积相关技术:
先导包:
import numpy as np
import h5py
import matplotlib.pyplot as plt
首先是padding,我们使用numpy提供的pad参数来进行padding操作,需要传的几个参数分别是array,然后就是三个维度上分别扩展多少位(arr3D为一个三维数组,我们不希望变成4维所以第一个均为0,然后第二维第三维前后分别加上几个0),然后constant表示填充:
# padding
arr3D = np.array([[[1, 1, 2, 2, 3, 4],
[1, 1, 2, 2, 3, 4],
[1, 1, 2, 2, 3, 4]],
[[0, 1, 2, 3, 4, 5],
[0, 1, 2, 3, 4, 5],
[0, 1, 2, 3, 4, 5]],
[[1, 1, 2, 2, 3, 4],
[1, 1, 2, 2, 3, 4],
[1, 1, 2, 2, 3, 4]]])
print('constant: \n' + str(np.pad(arr3D, ((0, 0), (1, 1), (2, 2)), 'constant')))
输出:
constant:
[[[0 0 0 0 0 0 0 0 0 0]
[0 0 1 1 2 2 3 4 0 0]
[0 0 1 1 2 2 3 4 0 0]
[0 0 1 1 2 2 3 4 0 0]
[0 0 0 0 0 0 0 0 0 0]]
[[0 0 0 0 0 0 0 0 0 0]
[0 0 0 1 2 3 4 5 0 0]
[0 0 0 1 2 3 4 5 0 0]
[0 0 0 1 2 3 4 5 0 0]
[0 0 0 0 0 0 0 0 0 0]]
[[0 0 0 0 0 0 0 0 0 0]
[0 0 1 1 2 2 3 4 0 0]
[0 0 1 1 2 2 3 4 0 0]
[0 0 1 1 2 2 3 4 0 0]
[0 0 0 0 0 0 0 0 0 0]]]我们试着可视化一下:
def zero_pad(X, pad):
"""
对图片X进行填充
:param X:
:param pad:
:return:
"""
X_paded = np.pad(X, (
(0, 0), # 样本数,不填充
(pad, pad), # 图像高度,你可以视为上面填充x个,下面填充y个(x,y)
(pad, pad), # 图像宽度,你可以视为左边填充x个,右边填充y个(x,y)
(0, 0)), # 通道数,不填充
'constant', constant_values=0) # 连续一样的值填充
return X_paded
np.random.seed(1)
x = np.random.randn(4, 3, 3, 2)
x_paded = zero_pad(x, 2)
#
# # 绘制图
fig, axarr = plt.subplots(1, 2) # 一行两列
axarr[0].set_title('x')
axarr[0].imshow(x[0, :, :, 0])
axarr[1].set_title('x_paded')
axarr[1].imshow(x_paded[0, :, :, 0])
plt.show()
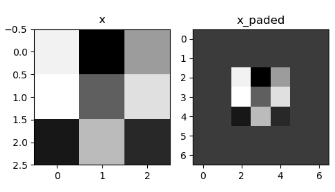
然后就是卷积操作,卷积操作的动图如下:
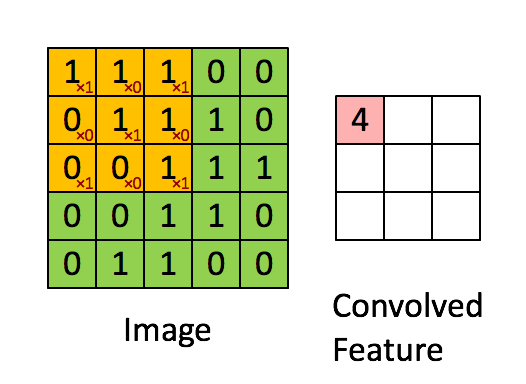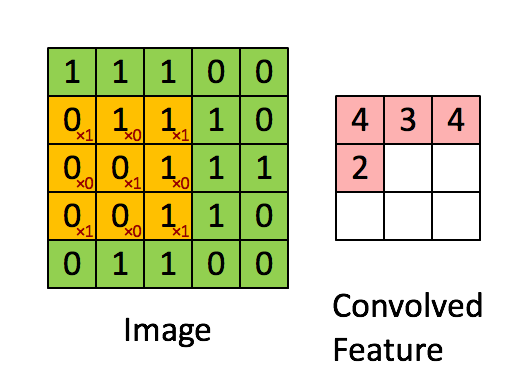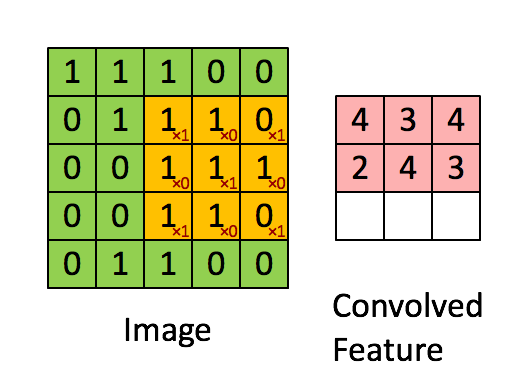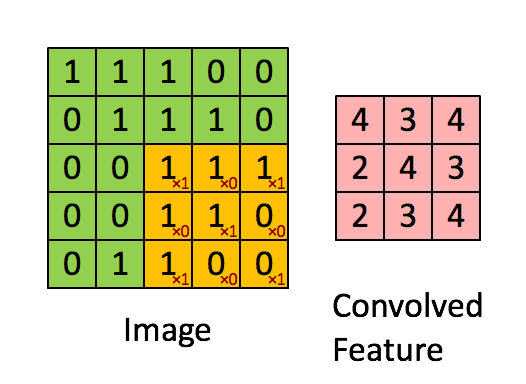
计算卷积后图片大小公式如下:
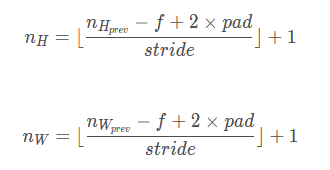
def conv_single_step(a_slice_prev, W, b):
"""
进行卷积操作
:param a_slice_prev:
:param W:
:param b:
:return:
"""
s = np.multiply(a_slice_prev, W) + b
Z = np.sum(s)
return Z
def conv_forward(A_prev, W, b, hparameters):
"""
卷积前向传播
:param A_prev:
:param W:
:param b:
:param hparameters:
:return:
"""
# 获取来自上一层数据的基本信息
(m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
# 获取权重矩阵的基本信息
(f, f, n_C_prev, n_C) = W.shape
# 获取超参值
stride = hparameters["stride"]
pad = hparameters["pad"]
# 计算卷积后的图像的宽度高度,参考上面的公式,使用int()来进行板除
n_H = int((n_H_prev - f + 2 * pad) / stride) + 1
n_W = int((n_W_prev - f + 2 * pad) / stride) + 1
# 使用0来初始化卷积输出Z
Z = np.zeros((m, n_H, n_W, n_C))
# 通过A_prev创建填充过了的A_prev_pad
A_prev_pad = zero_pad(A_prev, pad)
for i in range(m): # 遍历样本
a_prev_pad = A_prev_pad[i] # 选择第i个样本的扩充后的激活矩阵
for h in range(n_H): # 在输出的垂直轴上循环
for w in range(n_W): # 在输出的水平轴上循环
for c in range(n_C): # 循环遍历输出的通道
# 定位当前的切片位置
vert_start = h * stride # 竖向,开始的位置
vert_end = vert_start + f # 竖向,结束的位置
horiz_start = w * stride # 横向,开始的位置
horiz_end = horiz_start + f # 横向,结束的位置
# 切片位置定位好了我们就把它取出来,需要注意的是我们是“穿透”取出来的,
# 自行脑补一下吸管插入一层层的橡皮泥就明白了
a_slice_prev = a_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :]
# 执行单步卷积
Z[i, h, w, c] = conv_single_step(a_slice_prev, W[:, :, :, c], b[0, 0, 0, c])
# 数据处理完毕,验证数据格式是否正确
assert (Z.shape == (m, n_H, n_W, n_C))
# 存储一些缓存值,以便于反向传播使用
cache = (A_prev, W, b, hparameters)
return (Z, cache)
然后就是池化层:
def pool_forward(A_prev, hparameters, mode="max"):
"""
池化层
:param A_prev:
:param hparameters:
:param mode:
:return:
"""
# 获取输入数据的基本信息
(m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
# 获取超参数的信息
f = hparameters["f"]
stride = hparameters["stride"]
# 计算输出维度
n_H = int((n_H_prev - f) / stride) + 1
n_W = int((n_W_prev - f) / stride) + 1
n_C = n_C_prev
# 初始化输出矩阵
A = np.zeros((m, n_H, n_W, n_C))
for i in range(m): # 遍历样本
for h in range(n_H): # 在输出的垂直轴上循环
for w in range(n_W): # 在输出的水平轴上循环
for c in range(n_C): # 循环遍历输出的通道
# 定位当前的切片位置
vert_start = h * stride # 竖向,开始的位置
vert_end = vert_start + f # 竖向,结束的位置
horiz_start = w * stride # 横向,开始的位置
horiz_end = horiz_start + f # 横向,结束的位置
# 定位完毕,开始切割
a_slice_prev = A_prev[i, vert_start:vert_end, horiz_start:horiz_end, c]
# 对切片进行池化操作
if mode == "max":
A[i, h, w, c] = np.max(a_slice_prev)
elif mode == "average":
A[i, h, w, c] = np.mean(a_slice_prev)
# 池化完毕,校验数据格式
assert (A.shape == (m, n_H, n_W, n_C))
# 校验完毕,开始存储用于反向传播的值
cache = (A_prev, hparameters)
return A, cache
然后就是卷积的反向传播:
def conv_backward(dZ, cache):
"""
卷积层反向传播
:param dZ:
:param cache:
:return:
"""
# 获取cache的值
(A_prev, W, b, hparameters) = cache
# 获取A_prev的基本信息
(m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
# 获取dZ的基本信息
(m, n_H, n_W, n_C) = dZ.shape
# 获取权值的基本信息
(f, f, n_C_prev, n_C) = W.shape
# 获取hparaeters的值
pad = hparameters["pad"]
stride = hparameters["stride"]
# 初始化各个梯度的结构
dA_prev = np.zeros((m, n_H_prev, n_W_prev, n_C_prev))
dW = np.zeros((f, f, n_C_prev, n_C))
db = np.zeros((1, 1, 1, n_C))
# 前向传播中我们使用了pad,反向传播也需要使用,这是为了保证数据结构一致
A_prev_pad = zero_pad(A_prev, pad)
dA_prev_pad = zero_pad(dA_prev, pad)
# 现在处理数据
for i in range(m):
# 选择第i个扩充了的数据的样本,降了一维。
a_prev_pad = A_prev_pad[i]
da_prev_pad = dA_prev_pad[i]
for h in range(n_H):
for w in range(n_W):
for c in range(n_C):
# 定位切片位置
vert_start = h
vert_end = vert_start + f
horiz_start = w
horiz_end = horiz_start + f
# 定位完毕,开始切片
a_slice = a_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :]
# 切片完毕,使用上面的公式计算梯度
da_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :] += W[:, :, :, c] * dZ[i, h, w, c]
dW[:, :, :, c] += a_slice * dZ[i, h, w, c]
db[:, :, :, c] += dZ[i, h, w, c]
# 设置第i个样本最终的dA_prev,即把非填充的数据取出来。
dA_prev[i, :, :, :] = da_prev_pad[pad:-pad, pad:-pad, :]
# 数据处理完毕,验证数据格式是否正确
assert (dA_prev.shape == (m, n_H_prev, n_W_prev, n_C_prev))
return (dA_prev, dW, db)
然后是池化层的反向传播,因为对于最大池化层我们要记录最大的位置以便我们反向传播,因此需要多一个方法来记录这些最大值的位置:
def create_mask_from_window(x):
"""
从输入矩阵中创建掩码,以保存最大值的矩阵的位置。
:param x:
:return:
"""
mask = x == np.max(x)
return mask
def distribute_value(dz, shape):
"""
平均池化的反向传播
:param dz:
:param shape:
:return:
"""
# 获取矩阵的大小
(n_H, n_W) = shape
# 计算平均值
average = dz / (n_H * n_W)
# 填充入矩阵
a = np.ones(shape) * average
return a
def pool_backward(dA, cache, mode="max"):
"""
实现池化层的反向传播
:param dA:
:param cache:
:param mode:
:return:
"""
# 获取cache中的值
(A_prev, hparaeters) = cache
# 获取hparaeters的值
f = hparaeters["f"]
stride = hparaeters["stride"]
# 获取A_prev和dA的基本信息
(m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
(m, n_H, n_W, n_C) = dA.shape
# 初始化输出的结构
dA_prev = np.zeros_like(A_prev)
# 开始处理数据
for i in range(m):
a_prev = A_prev[i]
for h in range(n_H):
for w in range(n_W):
for c in range(n_C):
# 定位切片位置
vert_start = h
vert_end = vert_start + f
horiz_start = w
horiz_end = horiz_start + f
# 选择反向传播的计算方式
if mode == "max":
# 开始切片
a_prev_slice = a_prev[vert_start:vert_end, horiz_start:horiz_end, c]
# 创建掩码
mask = create_mask_from_window(a_prev_slice)
# 计算dA_prev,就是只在最大值的位置进行加减
dA_prev[i, vert_start:vert_end, horiz_start:horiz_end, c] += np.multiply(mask, dA[i, h, w, c])
elif mode == "average":
# 获取dA的值
da = dA[i, h, w, c]
# 定义过滤器大小
shape = (f, f)
# 平均分配
dA_prev[i, vert_start:vert_end, horiz_start:horiz_end, c] += distribute_value(da, shape)
# 数据处理完毕,开始验证格式
assert (dA_prev.shape == A_prev.shape)
return dA_prev
到这基本上我们就手动的写了一边卷积神经网络。
然后我们使用TensorFlow框架进行手势识别:
首先还是导包:
import math
import numpy as np
import h5py
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import tensorflow as tf
from tensorflow.python.framework import ops
from course_4_week_1 import cnn_utils
读取数据:
np.random.seed(1)
X_train_orig, Y_train_orig, X_test_orig, Y_test_orig, classes = cnn_utils.load_dataset()
然后进行数据标准化:
# 数据标准化
X_train = X_train_orig / 255
X_test = X_test_orig / 255
Y_train = cnn_utils.convert_to_one_hot(Y_train_orig, 6).T
Y_test = cnn_utils.convert_to_one_hot(Y_test_orig, 6).T
初始化我们的palceholder:
def create_placeholders(n_H0, n_W0, n_C0, n_y):
"""
创建占位符
:param n_H0:
:param n_W0:
:param n_C0:
:param n_y:
:return:
"""
X = tf.placeholder(tf.float32, [None, n_H0, n_W0, n_C0])
Y = tf.placeholder(tf.float32, [None, n_y])
return X, Y
初始化参数:
def initialize_parameters():
"""
初始化权值矩阵,这里我们把权值矩阵硬编码:
:return:
"""
W1 = tf.get_variable("W1", [4, 4, 3, 8], initializer=tf.contrib.layers.xavier_initializer(seed=1))
W2 = tf.get_variable("W2", [2, 2, 8, 16], initializer=tf.contrib.layers.xavier_initializer(seed=1))
parameters = {"W1": W1,
"W2": W2}
return parameters
然后对网络的前向传播进行定义:
def forward_propagation(X, parameters):
"""
实现前向传播
CONV2D -> RELU -> MAXPOOL -> CONV2D -> RELU -> MAXPOOL -> FLATTEN -> FULLYCONNECTED
:param X:
:param parameters:
:return:
"""
W1 = parameters['W1']
W2 = parameters['W2']
# Conv2d : 步伐:1,填充方式:“SAME”
Z1 = tf.nn.conv2d(X, W1, strides=[1, 1, 1, 1], padding="SAME")
# ReLU :
A1 = tf.nn.relu(Z1)
# Max pool : 窗口大小:8x8,步伐:8x8,填充方式:“SAME”
P1 = tf.nn.max_pool(A1, ksize=[1, 8, 8, 1], strides=[1, 8, 8, 1], padding="SAME")
# Conv2d : 步伐:1,填充方式:“SAME”
Z2 = tf.nn.conv2d(P1, W2, strides=[1, 1, 1, 1], padding="SAME")
# ReLU :
A2 = tf.nn.relu(Z2)
# Max pool : 过滤器大小:4x4,步伐:4x4,填充方式:“SAME”
P2 = tf.nn.max_pool(A2, ksize=[1, 4, 4, 1], strides=[1, 4, 4, 1], padding="SAME")
# 一维化上一层的输出
P = tf.contrib.layers.flatten(P2)
# 全连接层(FC):使用没有非线性激活函数的全连接层
Z3 = tf.contrib.layers.fully_connected(P, 6, activation_fn=None)
return Z3
计算代价:
def compute_cost(Z3, Y):
"""
计算代价
:param Z3:
:param Y:
:return:
"""
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=Z3, labels=Y))
return cost
然后我们定义模型并运行:
def model(X_train, Y_train, X_test, Y_test, learning_rate=0.009,
num_epochs=100, minibatch_size=64, print_cost=True, isPlot=True):
"""
创建模型
:param X_train:
:param Y_train:
:param X_test:
:param Y_test:
:param learning_rate:
:param num_epochs:
:param minibatch_size:
:param print_cost:
:param isPlot:
:return:
"""
tf.get_default_graph()
seed = 3
tf.set_random_seed(1)
# m个图片 h*w大小 c个卷积层
m, n_H0, n_W0, n_C0 = X_train.shape
# 有多少种结果
n_y = Y_train.shape[1]
costs = []
X, Y = create_placeholders(n_H0, n_W0, n_C0, n_y)
# 初始化参数
parameters = initialize_parameters()
# 前向传播
Z3 = forward_propagation(X, parameters)
# 计算成本
cost = compute_cost(Z3, Y)
# 反向传播
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost)
# 保存数据
saver = tf.train.Saver()
# 全局初始化变量
init = tf.global_variables_initializer()
# 开始运行
with tf.Session() as session:
# 初始化参数
session.run(init)
# 遍历数据
for epoch in range(num_epochs):
minibatch_cost = 0
num_minibatches = int(m / minibatch_size)
seed = seed + 1
minibatches = cnn_utils.random_mini_batches(X_train, Y_train, minibatch_size, seed)
for minibatch in minibatches:
minibatch_X, minibatch_Y = minibatch
_, temp_cost = session.run([optimizer, cost], feed_dict={X: minibatch_X, Y: minibatch_Y})
minibatch_cost += temp_cost / num_minibatches
# 保存参数
saver.save(session, './model/my_model', global_step=5)
# 打印成本
if print_cost:
if epoch % 5 == 0:
print("当前是第 " + str(epoch) + " 代,成本值为:" + str(minibatch_cost))
# 记录成本
costs.append(minibatch_cost)
# 绘制成本曲线
if isPlot:
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
# 开始预测
predict_op = tf.argmax(Z3, 1)
corrent_prediction = tf.equal(predict_op, tf.argmax(Y, 1))
accuracy = tf.reduce_mean(tf.cast(corrent_prediction, 'float',name='accuracy'))
print("corrent_prediction accuracy= " + str(accuracy))
train_accuracy = accuracy.eval({X: X_train, Y: Y_train})
test_accuracy = accuracy.eval({X: X_test, Y: Y_test})
print("训练集准确度:" + str(train_accuracy))
print("测试集准确度:" + str(test_accuracy))
return train_accuracy, test_accuracy, parameters
_, _, parameters = model(X_train, Y_train, X_test, Y_test, num_epochs=150)
程序输出如下:
当前是第 0 代,成本值为:1.9079020842909813
当前是第 5 代,成本值为:1.8338764905929565
当前是第 10 代,成本值为:1.3530711755156517
当前是第 15 代,成本值为:1.0513618439435959
当前是第 20 代,成本值为:0.7954236306250095
当前是第 25 代,成本值为:0.6776404492557049
当前是第 30 代,成本值为:0.6062654200941324
当前是第 35 代,成本值为:0.5560709461569786
当前是第 40 代,成本值为:0.50390131957829
当前是第 45 代,成本值为:0.45013799145817757
当前是第 50 代,成本值为:0.43954286724328995
当前是第 55 代,成本值为:0.3888242533430457
当前是第 60 代,成本值为:0.37428596522659063
当前是第 65 代,成本值为:0.35892391856759787
当前是第 70 代,成本值为:0.33011145144701004
当前是第 75 代,成本值为:0.3231000145897269
当前是第 80 代,成本值为:0.31615445110946894
当前是第 85 代,成本值为:0.3158330311998725
当前是第 90 代,成本值为:0.26991996727883816
当前是第 95 代,成本值为:0.2658209102228284
当前是第 100 代,成本值为:0.2894991096109152
当前是第 105 代,成本值为:0.24726102221757174
当前是第 110 代,成本值为:0.2515424760058522
当前是第 115 代,成本值为:0.3262146320194006
当前是第 120 代,成本值为:0.23388438019901514
当前是第 125 代,成本值为:0.23200181871652603
当前是第 130 代,成本值为:0.2730541517958045
当前是第 135 代,成本值为:0.22053561871871352
当前是第 140 代,成本值为:0.25617739744484425
当前是第 145 代,成本值为:0.19133262312971056
corrent_prediction accuracy= Tensor("Mean_1:0", shape=(), dtype=float32)
训练集准确度:0.93796295
测试集准确度:0.81666666
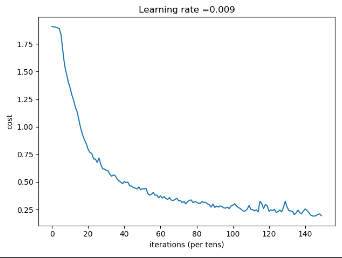
完整代码:
# -*- coding:utf-8 -*-
"""
┏┛ ┻━━━━━┛ ┻┓
┃ ┃
┃ ━ ┃
┃ ┳┛ ┗┳ ┃
┃ ┃
┃ ┻ ┃
┃ ┃
┗━┓ ┏━━━┛
┃ ┃ 神兽保佑
┃ ┃ 代码无BUG!
┃ ┗━━━━━━━━━┓
┃ ┣┓
┃ ┏┛
┗━┓ ┓ ┏━━━┳ ┓ ┏━┛
┃ ┫ ┫ ┃ ┫ ┫
┗━┻━┛ ┗━┻━┛
"""
import math
import numpy as np
import h5py
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import tensorflow as tf
from tensorflow.python.framework import ops
from course_4_week_1 import cnn_utils
np.random.seed(1)
X_train_orig, Y_train_orig, X_test_orig, Y_test_orig, classes = cnn_utils.load_dataset()
# index = 6
# plt.imshow(X_train_orig[index])
# print("y = " + str(np.squeeze(Y_train_orig[:, index])))
# plt.show()
# 数据标准化
X_train = X_train_orig / 255
X_test = X_test_orig / 255
Y_train = cnn_utils.convert_to_one_hot(Y_train_orig, 6).T
Y_test = cnn_utils.convert_to_one_hot(Y_test_orig, 6).T
conv_layers = {}
def create_placeholders(n_H0, n_W0, n_C0, n_y):
"""
创建占位符
:param n_H0:
:param n_W0:
:param n_C0:
:param n_y:
:return:
"""
X = tf.placeholder(tf.float32, [None, n_H0, n_W0, n_C0])
Y = tf.placeholder(tf.float32, [None, n_y])
return X, Y
def initialize_parameters():
"""
初始化权值矩阵,这里我们把权值矩阵硬编码:
:return:
"""
W1 = tf.get_variable("W1", [4, 4, 3, 8], initializer=tf.contrib.layers.xavier_initializer(seed=1))
W2 = tf.get_variable("W2", [2, 2, 8, 16], initializer=tf.contrib.layers.xavier_initializer(seed=1))
parameters = {"W1": W1,
"W2": W2}
return parameters
def forward_propagation(X, parameters):
"""
实现前向传播
CONV2D -> RELU -> MAXPOOL -> CONV2D -> RELU -> MAXPOOL -> FLATTEN -> FULLYCONNECTED
:param X:
:param parameters:
:return:
"""
W1 = parameters['W1']
W2 = parameters['W2']
# Conv2d : 步伐:1,填充方式:“SAME”
Z1 = tf.nn.conv2d(X, W1, strides=[1, 1, 1, 1], padding="SAME")
# ReLU :
A1 = tf.nn.relu(Z1)
# Max pool : 窗口大小:8x8,步伐:8x8,填充方式:“SAME”
P1 = tf.nn.max_pool(A1, ksize=[1, 8, 8, 1], strides=[1, 8, 8, 1], padding="SAME")
# Conv2d : 步伐:1,填充方式:“SAME”
Z2 = tf.nn.conv2d(P1, W2, strides=[1, 1, 1, 1], padding="SAME")
# ReLU :
A2 = tf.nn.relu(Z2)
# Max pool : 过滤器大小:4x4,步伐:4x4,填充方式:“SAME”
P2 = tf.nn.max_pool(A2, ksize=[1, 4, 4, 1], strides=[1, 4, 4, 1], padding="SAME")
# 一维化上一层的输出
P = tf.contrib.layers.flatten(P2)
# 全连接层(FC):使用没有非线性激活函数的全连接层
Z3 = tf.contrib.layers.fully_connected(P, 6, activation_fn=None)
return Z3
def compute_cost(Z3, Y):
"""
计算代价
:param Z3:
:param Y:
:return:
"""
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=Z3, labels=Y))
return cost
def model(X_train, Y_train, X_test, Y_test, learning_rate=0.009,
num_epochs=100, minibatch_size=64, print_cost=True, isPlot=True):
"""
创建模型
:param X_train:
:param Y_train:
:param X_test:
:param Y_test:
:param learning_rate:
:param num_epochs:
:param minibatch_size:
:param print_cost:
:param isPlot:
:return:
"""
tf.get_default_graph()
seed = 3
tf.set_random_seed(1)
# m个图片 h*w大小 c个卷积层
m, n_H0, n_W0, n_C0 = X_train.shape
# 有多少种结果
n_y = Y_train.shape[1]
costs = []
X, Y = create_placeholders(n_H0, n_W0, n_C0, n_y)
# 初始化参数
parameters = initialize_parameters()
# 前向传播
Z3 = forward_propagation(X, parameters)
# 计算成本
cost = compute_cost(Z3, Y)
# 反向传播
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(cost)
# 保存数据
saver = tf.train.Saver()
# 全局初始化变量
init = tf.global_variables_initializer()
# 开始运行
with tf.Session() as session:
# 初始化参数
session.run(init)
# 遍历数据
for epoch in range(num_epochs):
minibatch_cost = 0
num_minibatches = int(m / minibatch_size)
seed = seed + 1
minibatches = cnn_utils.random_mini_batches(X_train, Y_train, minibatch_size, seed)
for minibatch in minibatches:
minibatch_X, minibatch_Y = minibatch
_, temp_cost = session.run([optimizer, cost], feed_dict={X: minibatch_X, Y: minibatch_Y})
minibatch_cost += temp_cost / num_minibatches
# 保存参数
saver.save(session, './model/my_model', global_step=5)
# 打印成本
if print_cost:
if epoch % 5 == 0:
print("当前是第 " + str(epoch) + " 代,成本值为:" + str(minibatch_cost))
# 记录成本
costs.append(minibatch_cost)
# 绘制成本曲线
if isPlot:
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
# 开始预测
predict_op = tf.argmax(Z3, 1)
corrent_prediction = tf.equal(predict_op , tf.argmax(Y, 1))
accuracy = tf.reduce_mean(tf.cast(corrent_prediction, 'float',name='accuracy'))
print("corrent_prediction accuracy= " + str(accuracy))
train_accuracy = accuracy.eval({X: X_train, Y: Y_train})
test_accuracy = accuracy.eval({X: X_test, Y: Y_test})
print("训练集准确度:" + str(train_accuracy))
print("测试集准确度:" + str(test_accuracy))
return train_accuracy, test_accuracy, parameters
_, _, parameters = model(X_train, Y_train, X_test, Y_test, num_epochs=150)
"""
当前是第 0 代,成本值为:1.9079020842909813
当前是第 5 代,成本值为:1.8338764905929565
当前是第 10 代,成本值为:1.3530711755156517
当前是第 15 代,成本值为:1.0513618439435959
当前是第 20 代,成本值为:0.7954236306250095
当前是第 25 代,成本值为:0.6776404492557049
当前是第 30 代,成本值为:0.6062654200941324
当前是第 35 代,成本值为:0.5560709461569786
当前是第 40 代,成本值为:0.50390131957829
当前是第 45 代,成本值为:0.45013799145817757
当前是第 50 代,成本值为:0.43954286724328995
当前是第 55 代,成本值为:0.3888242533430457
当前是第 60 代,成本值为:0.37428596522659063
当前是第 65 代,成本值为:0.35892391856759787
当前是第 70 代,成本值为:0.33011145144701004
当前是第 75 代,成本值为:0.3231000145897269
当前是第 80 代,成本值为:0.31615445110946894
当前是第 85 代,成本值为:0.3158330311998725
当前是第 90 代,成本值为:0.26991996727883816
当前是第 95 代,成本值为:0.2658209102228284
当前是第 100 代,成本值为:0.2894991096109152
当前是第 105 代,成本值为:0.24726102221757174
当前是第 110 代,成本值为:0.2515424760058522
当前是第 115 代,成本值为:0.3262146320194006
当前是第 120 代,成本值为:0.23388438019901514
当前是第 125 代,成本值为:0.23200181871652603
当前是第 130 代,成本值为:0.2730541517958045
当前是第 135 代,成本值为:0.22053561871871352
当前是第 140 代,成本值为:0.25617739744484425
当前是第 145 代,成本值为:0.19133262312971056
corrent_prediction accuracy= Tensor("Mean_1:0", shape=(), dtype=float32)
训练集准确度:0.93796295
测试集准确度:0.81666666
"""
0 条评论