吴恩达深度学习第四课第二周:深度卷积网络:实例探究
注:所有代码均可在github获得完整文件。

1.经典网络
首先介绍几个经典的卷积神经网络,他们分别是LeNet-5、AlexNet和VGGNet。
LeNet-5:假设我们有一张32*32*1的图片,leNet-5可以识别图中的手写数字。因为 leNet-5 针对的是灰度图片训练,因此图片大小只有32*32*1.它使用6个5*5的过滤器,步幅为1,padding为0,因此输出大小为28*28,然后进行池化操作。
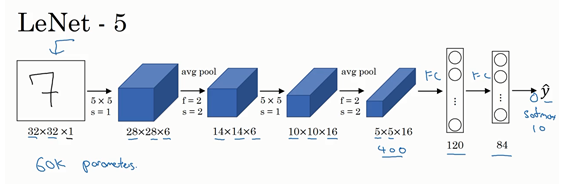
这个网络大概有6w个参数。
AlexNet:首先用一张227*227*3的图片作为输入,第一层我们使用96个11*11的过滤器,步幅为4,因此图片缩小到55*55.然后用一个3*3的最大池化层,f=3,步幅为2,卷积层大小变为27*27*96,然后再执行一个5*5的卷积,padding之后输出依然是27*27*256,然后继续最大池化层变成13*13*256
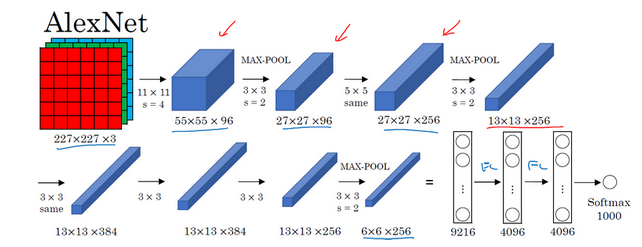
然后进行三次3*3的same卷积变成13*13*256然后进行一个最大池化层变成6*6*256最后是三个全连接层。
AlexNet 包括了大约6000w个参数。
VGG-16: VGG-16 的超参比较少,是一种只需专注于构建卷积层的简单网络。
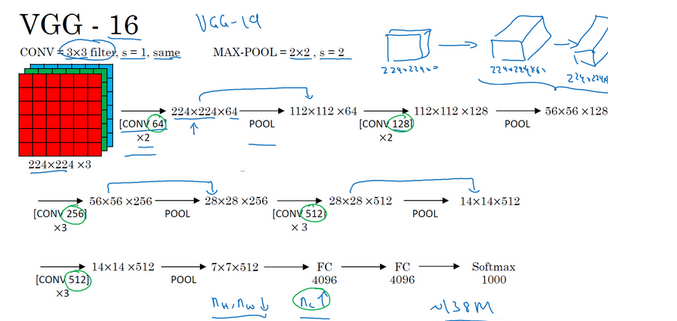
正是设计此种网络结构的另一个简单原则。这种相对一致的网络结构对研究者很有吸引力,而它的主要缺点是需要训练的特征数量非常巨大。
2.残差网络
对于很深的网络是很难训练的,主要原因是存在梯度消失和梯度爆炸的问题。而残差网络则可以一定程度上解决这种问题。
残差网络实际上是多个下图中的块组成:
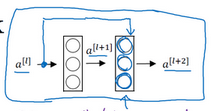
由于添加了一条可以跳过一层网络的参数,而这层参数也是经过反向传播学习来的,因此可以更好地匹配数据。
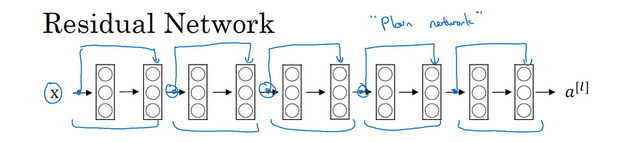
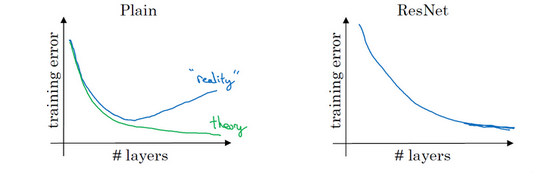
我们知道一般认为随着网络层数的加大,代价应该如左图绿线一样,但是实际上是蓝线,并没有达到我们预期的绿线水平,而使用残差网络则可以达到右图的样子。
3.网络中的网络以及1*1卷积
如下图就是一个1*1卷积的示意图
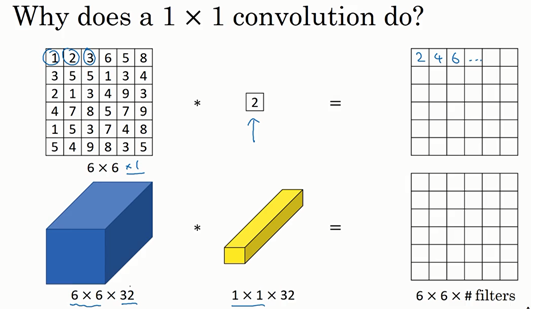
那么1*1的卷积有什么用呢?
我们用1*1的卷积计算出结果的一个1*1位置,也就是相当于做了一层全连接
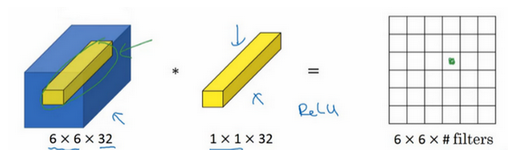
而如果我们使用多个1*1卷积,我们也就可以得到多个个channel的结果
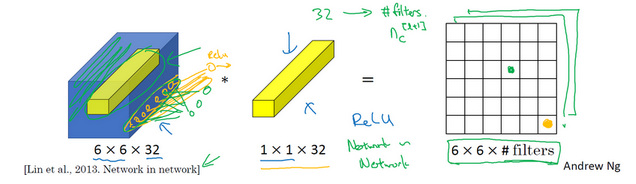
因此我们可以用1*1的卷积用来压缩特征
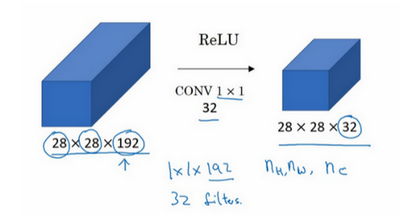
4.谷歌Inception网络简介
Inception 盗梦空间。
这个网络之所以叫这么梦幻的一个名字就是因为这个网络确实挺梦幻,他还有一个名字叫做GoogleLeNet,是向LeNet网络致敬。
这个网络我们不再进行卷积大小的选择,而是由网络进行选择,我们将每一种情况都放到一起:
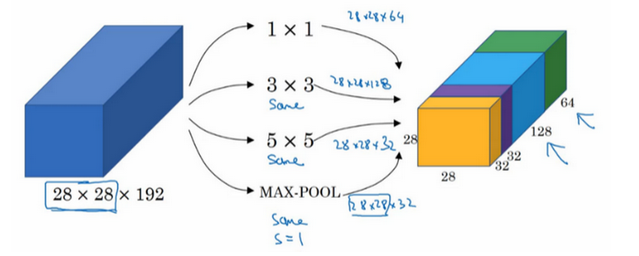
如果我们简单的28*28*192的变成28*28*32,我们需要计算1.2e词
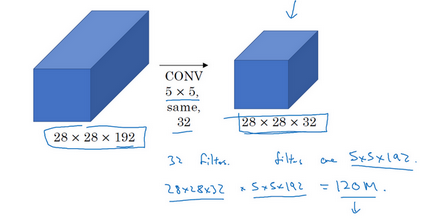
而如果我们使用1*1卷积
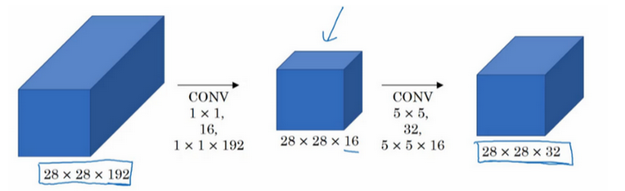
这时候我们只需要计算1200w,大概是上一种的十分之一,因此第二种显然是比较好的方法,又因为中间加了一个较小的卷积,因此也被形象的叫做瓶颈层。
那么这个网络是什么样子的呢?
我们已经看过基本的样子:
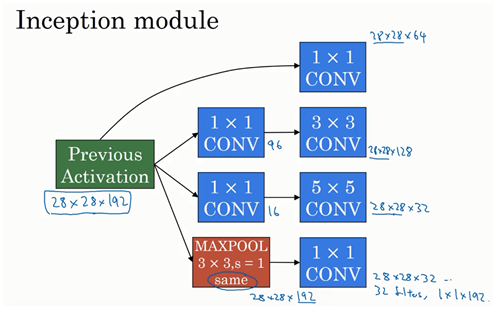
然后将多个这个模块拼接起来:
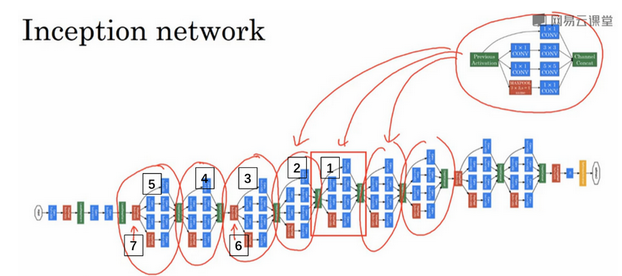
实际上真正的网络比这个还多一点东西,就是更多的输出:
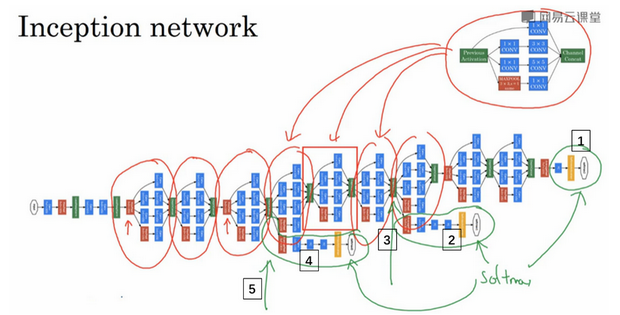
这样通过隐藏层来进行预测,可以找出更好的网络结构。
测验
1. 在典型的卷积神经网络中,随着网络的深度增加,你能看到的现象是?
- nH 和 nW 增加,同时nC 减少。
- nH 和 nW 减少,同时 nC 也减少。
- nH 和 nW 增加,同时 nC 也增加。
- nH 和 nW 减少,同时 nC 增加。
4。
2. 在典型的卷积神经网络中,你能看到的是?
- 多个卷积层后面跟着的是一个池化层。
- 多个池化层后面跟着的是一个卷积层。
- 全连接层(FC)位于最后的几层。
- 全连接层(FC)位于开始的几层。
2,4。
3. 为了构建一个非常深的网络,我们经常在卷积层使用“valid”的填充,只使用池化层来缩小激活值的宽/高度,否则的话就会使得输入迅速的变小。
错误。
4. 我们使用普通的网络结构来训练一个很深的网络,要使得网络适应一个很复杂的功能(比如增加层数),总会有更低的训练误差。
错误。
5. 面计算残差(ResNet)块的公式中,横线上应该分别填什么?
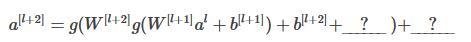
- 分别是 0 与 z[l+1] 。
- 分别是 a[l] 与 0
- 分别是 z[l] 与 a[l] 。
- 分别是 0 与 a[l] 。
2。
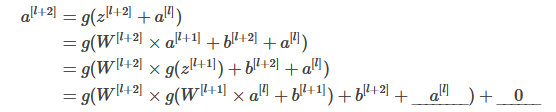
6. 关于残差网络下面哪个(些)说法是正确的?
- 使用跳越连接能够对反向传播的梯度下降有益且能够帮你对更深的网络进行训练。
- 跳跃连接计算输入的复杂的非线性函数以传递到网络中的更深层。
- 有L层的残差网络一共有L2种跳跃连接的顺序。
- 跳跃连接能够使得网络轻松地学习残差块类的输入输出间的身份映射。
2,4。
7. 假设你的输入的维度为64x64x16,单个1×1的卷积过滤器含有多少个参数(包括偏差)?
16+1。
8. 假设你有一个维度为nH×nW×nC的卷积输入,下面哪个说法是正确的(假设卷积层为1×1,步伐为1,padding为0)?
- 你能够使用1×1的卷积层来减少nC,但是不能减少 nH、nW
- 你可以使用池化层减少 nH、nW,但是不能减少 nC
- 你可以使用一个1×1的卷积层来减少nH、nW和nC.
- 你可以使用池化层减少 nH、 nW和nC.
1,2。
9. 关于 Inception 网络下面哪些说法是正确的
- Inception 网络包含了各种网络的体系结构(类似于随机删除节点模式,它会在每一步中随机选择网络的结构),因此它具有随机删除节点的正则化效应。
- Inception 块通常使用1×1的卷积来减少输入卷积的大小,然后再使用3×3和5×5的卷积。
- 一个inception 块允许网络使用1×1, 3×3, 5×5 的和卷积个池化层的组合。
- 通过叠加inception块的方式让inception 网络更深不会损害训练集的表现。
2,3。
10. 下面哪些是使用卷积网络的开源实现(包含模型/权值)的常见原因?
- 为一个计算机视觉任务训练的模型通常可以用来数据扩充,即使对于不同的计算机视觉任务也是如此。
- 为一个计算机视觉任务训练的参数通常对其他计算机视觉任务的预训练是有用的。
- 使用获得计算机视觉竞赛奖项的相同的技术,广泛应用于实际部署。
- 使用开源实现可以很简单的来实现复杂的卷积结构。
2,3,4。
编程作业
这一周的作业主要是keras入门和ResNet网络。
首先我们做keras入门,思考如下情绪识别任务:

在开始之前建议先简单看一下文档:
首先是导包:
import keras
from course_4_week_2 import kt_utils
import keras.backend as K
K.set_image_data_format('channels_last')
然后是读取数据和数据标准化:
X_train_orig, Y_train_orig, X_test_orig, Y_test_orig, classes = kt_utils.load_dataset()
# 标准化数据
X_train = X_train_orig / 255.
X_test = X_test_orig / 255.
# reshape
Y_train = Y_train_orig.T
Y_test = Y_test_orig.T
定义模型:
def model(input_shape):
"""
总体模型
:param input_shape:
:return:
"""
# 定义输出的placeholder
X_input = keras.layers.Input(input_shape)
# 用0填充
X = keras.layers.ZeroPadding2D((3, 3))(X_input)
# CONV -> BN -> RELU
X = keras.layers.Conv2D(32, (7, 7), strides=(1, 1), name='conv0')(X)
X = keras.layers.BatchNormalization(axis=3, name='bn0')(X)
X = keras.layers.Activation('relu')(X)
# 最大池化层
X = keras.layers.MaxPool2D((2, 2), name='max_pool')(X)
# 降维,矩阵转换为向量+全连接
X = keras.layers.Flatten()(X) # 多维的输入一维化
X = keras.layers.Dense(1, activation='sigmoid', name='fc')(X) # 输出一个神经元 sigmoid激活
model = keras.models.Model(inputs=X_input, outputs=X, name='HappyModel')
return model
创建实体、训练和测试:
# 创建一个模型实体
happy_model = model(X_train.shape[1:])
# 编译模型
happy_model.compile('adam', 'binary_crossentropy', metrics=['accuracy'])
# 训练模型
happy_model.fit(X_train, Y_train, epochs=40, batch_size=50)
# 评估模型
preds = happy_model.evaluate(X_test, Y_test, batch_size=32, verbose=1, sample_weight=None) # verbose 日志级别
# 保存模型
happy_model.save('happy_model.h5')
print("误差值 = " + str(preds[0]))
print("准确度 = " + str(preds[1]))
最后输出(节选):
150/150 [==============================] - 1s 7ms/step
误差值 = 0.1285133997599284
准确度 = 0.9333333373069763
然后我们可以进行简单的测试:
import keras
from matplotlib.pyplot import imshow
import matplotlib.pyplot as plt
from keras.preprocessing import image
import numpy as np
img = image.load_img('./2.png', target_size=(64, 64))
imshow(img)
plt.show()
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
x = keras.applications.imagenet_utils.preprocess_input(x)
happy_model = keras.models.load_model('./resnet_model.h5')
print(happy_model.summary())
print(happy_model.predict(x))
然后可以看到下图,并有一个输出向量的输出
然后是残差网络ResNet。
首先导包:
import keras
from keras.models import Model
from keras.initializers import glorot_uniform
from course_4_week_2 import resnets_utils
import keras.backend as K
K.set_image_data_format('channels_last')
K.set_learning_phase(1)
我们先实现一个最小的残差块:
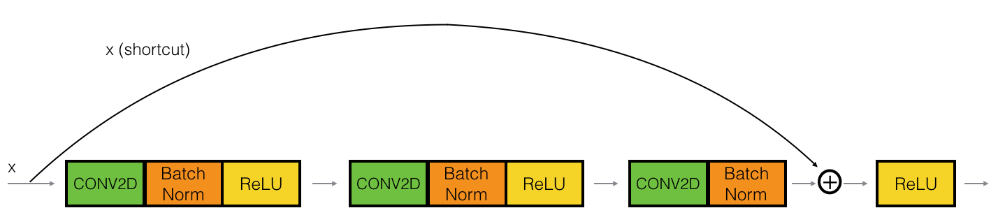
def identity_block(X, f, filters, stage, block):
"""
实现最小模块
:param X: 输入数据
:param f: CONV窗口维度
:param filters: 每层过滤器数量
:param stage: 层数(用来命名)
:param block: 字符串,用来命名
:return:
"""
# 定义命名
conv_name_base = 'res' + str(stage) + block + '_branch'
bn_name_base = 'bn' + str(stage) + block + '_branch'
# 获取过滤器数量
F1, F2, F3 = filters
# 保存输入数据,用于捷径
X_shortcut = X
# 第一部分
# 卷积层
X = keras.layers.Conv2D(filters=F1, kernel_size=(1, 1), strides=(1, 1), padding='valid', name=conv_name_base + '2a',
kernel_initializer=glorot_uniform(seed=0))(X)
# 归一化
X = keras.layers.BatchNormalization(axis=3, name=bn_name_base + '2a')(X)
# 激活
X = keras.layers.Activation('relu')(X)
# 第二部分
X = keras.layers.Conv2D(filters=F2, kernel_size=(f, f), strides=(1, 1), padding='same', name=conv_name_base + '2b',
kernel_initializer=glorot_uniform(seed=0))(X)
X = keras.layers.BatchNormalization(axis=3, name=bn_name_base + '2b')(X)
X = keras.layers.Activation('relu')(X)
# 第三部分
X = keras.layers.Conv2D(filters=F3, kernel_size=(1, 1), strides=(1, 1), padding='valid', name=conv_name_base + '2c',
kernel_initializer=glorot_uniform(seed=0))(X)
X = keras.layers.BatchNormalization(axis=3, name=bn_name_base + '2c')(X)
X = keras.layers.Activation('relu')(X)
# 将捷径加进来
X = keras.layers.Add()([X, X_shortcut])
X = keras.layers.Activation('relu')(X)
return X
对于从x经过几次卷积后维度发生变化的情况,我们在捷径中继续添加一个卷积层,来适配x和最后输出维度不同的问题。
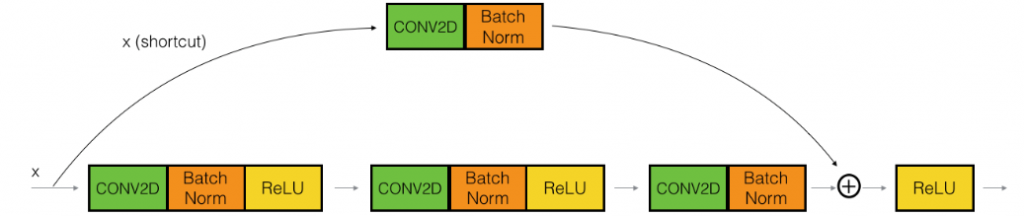
def convolutional_block(X, f, filters, stage, block, s=2):
"""
卷积块
:param X:
:param f:
:param fliters:
:param stage:
:param block:
:param s:
:return:
"""
# 定义命名规则
conv_name_base = 'res' + str(stage) + block + '_branch'
bn_name_base = 'bn' + str(stage) + block + '_branch'
# 获取过滤器数量
F1, F2, F3 = filters
# 保存输入数据
X_shortcut = X
# 第一部分
# 卷积层
X = keras.layers.Conv2D(filters=F1, kernel_size=(1, 1), strides=(s, s), padding='valid', name=conv_name_base + '2a',
kernel_initializer=glorot_uniform(seed=0))(X)
X = keras.layers.BatchNormalization(axis=3, name=bn_name_base + '2a')(X)
X = keras.layers.Activation('relu')(X)
# 第二部分
X = keras.layers.Conv2D(filters=F2, kernel_size=(f, f), strides=(1, 1), padding='same', name=conv_name_base + '2b',
kernel_initializer=glorot_uniform(seed=0))(X)
X = keras.layers.BatchNormalization(axis=3, name=bn_name_base + '2b')(X)
X = keras.layers.Activation('relu')(X)
# 第三部分
X = keras.layers.Conv2D(filters=F3, kernel_size=(1, 1), strides=(1, 1), padding='valid', name=conv_name_base + '2c',
kernel_initializer=glorot_uniform(seed=0))(X)
X = keras.layers.BatchNormalization(axis=3, name=bn_name_base + '2c')(X)
X = keras.layers.Activation('relu')(X)
# 捷径
X_shortcut = keras.layers.Conv2D(filters=F3, kernel_size=(1, 1), strides=(s, s), padding='valid',
name=conv_name_base + '1', kernel_initializer=glorot_uniform(seed=0))(X_shortcut)
X_shortcut = keras.layers.BatchNormalization(axis=3, name=bn_name_base + '1')(X_shortcut)
X = keras.layers.Add()([X, X_shortcut])
X = keras.layers.Activation('relu')(X)
return X
然后就到了构建模型主体,在这里我们定义了一个50层的神经网络(16个残差块,一个全连接层一个输出层):
def ResNet50(input_shape=(64, 64, 3), classes=6):
"""
50层的ResNet
:param input_shape:
:param classes:
:return:
"""
# 输入tensor
X_input = keras.layers.Input(input_shape)
# padding
X = keras.layers.ZeroPadding2D((3, 3))(X_input)
# stage1
X = keras.layers.Conv2D(filters=64, kernel_size=(7, 7), strides=(2, 2), name='conv1',
kernel_initializer=glorot_uniform(seed=0))(X)
X = keras.layers.BatchNormalization(axis=3, name='bn_conv1')(X)
X = keras.layers.Activation('relu')(X)
X = keras.layers.MaxPooling2D(pool_size=(3, 3), strides=(2, 2))(X)
# stage2
X = convolutional_block(X, f=3, filters=[64, 64, 256], stage=2, block="a", s=1)
X = identity_block(X, f=3, filters=[64, 64, 256], stage=2, block="b")
X = identity_block(X, f=3, filters=[64, 64, 256], stage=2, block="c")
# stage3
X = convolutional_block(X, f=3, filters=[128, 128, 512], stage=3, block="a", s=2)
X = identity_block(X, f=3, filters=[128, 128, 512], stage=3, block="b")
X = identity_block(X, f=3, filters=[128, 128, 512], stage=3, block="c")
X = identity_block(X, f=3, filters=[128, 128, 512], stage=3, block="d")
# stage4
X = convolutional_block(X, f=3, filters=[256, 256, 1024], stage=4, block="a", s=2)
X = identity_block(X, f=3, filters=[256, 256, 1024], stage=4, block="b")
X = identity_block(X, f=3, filters=[256, 256, 1024], stage=4, block="c")
X = identity_block(X, f=3, filters=[256, 256, 1024], stage=4, block="d")
X = identity_block(X, f=3, filters=[256, 256, 1024], stage=4, block="e")
X = identity_block(X, f=3, filters=[256, 256, 1024], stage=4, block="f")
# stage5
X = convolutional_block(X, f=3, filters=[512, 512, 2048], stage=5, block="a", s=2)
X = identity_block(X, f=3, filters=[512, 512, 2048], stage=5, block="b")
X = identity_block(X, f=3, filters=[512, 512, 2048], stage=5, block="c")
# 均值池化层
X = keras.layers.AveragePooling2D(pool_size=(2, 2), padding="same")(X)
# 输出层
X = keras.layers.Flatten()(X) # 多维的输入一维化
X = keras.layers.Dense(classes, activation="softmax", name="fc" + str(classes),
kernel_initializer=glorot_uniform(seed=0))(X)
# 创建模型
model = Model(inputs=X_input, outputs=X, name="ResNet50")
return model
最后就是模型的初始化、训练以及测试:
model = ResNet50(input_shape=(64, 64, 3), classes=6)
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
X_train_orig, Y_train_orig, X_test_orig, Y_test_orig, classes = resnets_utils.load_dataset()
# 标准化
X_train = X_train_orig / 255
X_test = X_test_orig / 255
Y_train = resnets_utils.convert_to_one_hot(Y_train_orig, 6).T
Y_test = resnets_utils.convert_to_one_hot(Y_test_orig, 6).T
model.fit(X_train, Y_train, epochs=2, batch_size=32)
preds = model.evaluate(X_test, Y_test, batch_size=32, verbose=1, sample_weight=None) # verbose 日志级别
# 保存模型
model.save('resnet_model.h5')
print("误差值 = " + str(preds[0]))
print("准确度 = " + str(preds[1]))
因为我们只训练了2批次,所以准确度相对比较低,输出(节选):
32/120 [=======>......................] - ETA: 4s
64/120 [===============>..............] - ETA: 2s
96/120 [=======================>......] - ETA: 0s
120/120 [==============================] - 4s 37ms/step
误差值 = 0.6602797726790111
准确度 = 0.7666666666666667
对于测试,和上面的卷及网络测试如出一辙,不得不说keras的测试还是人性化了不少:
import keras
from matplotlib.pyplot import imshow
import matplotlib.pyplot as plt
from keras.preprocessing import image
import numpy as np
img = image.load_img('./2.png', target_size=(64, 64))
imshow(img)
plt.show()
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
x = keras.applications.imagenet_utils.preprocess_input(x)
model = keras.models.load_model('./resnet_model.h5')
print(model.summary())
print(model.predict(x))
0 条评论