首先查看一下注意力的计算方式:
attention=Softmax(\frac{QK^T}{\sqrt{d_k}})V主要是有几个方面可以进行解释。
梯度传播
首先说梯度传播的问题,由于$attention$的计算使用了$Softmax$,而$Softmax$的曲线在输入值较大时,梯度接近$0$,最终导致梯度消失,如下图所示
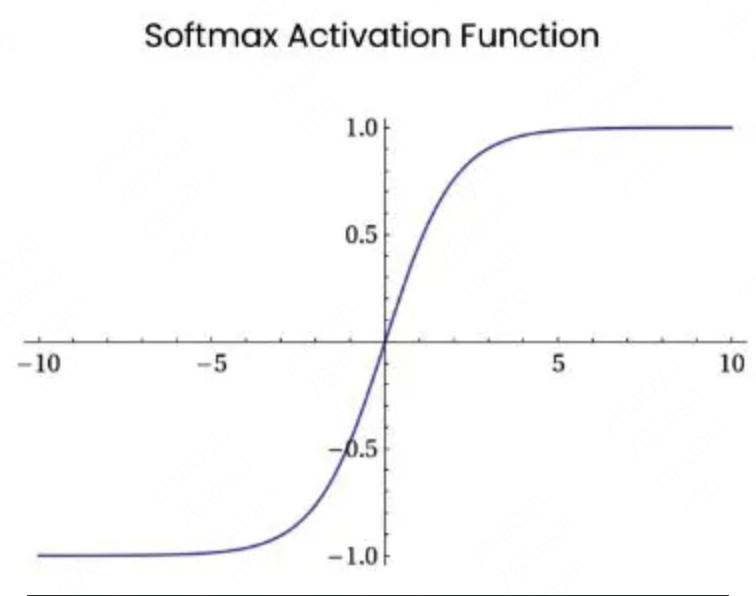
同时在进行矩阵运算时,由于矩阵运算的运算规则有相加的步骤,因此不可避免的每经过一次矩阵运算,矩阵内的值都会扩大矩阵维度这么大的倍数(比如下图大概会扩大3倍)。会导致梯度爆炸的问题。
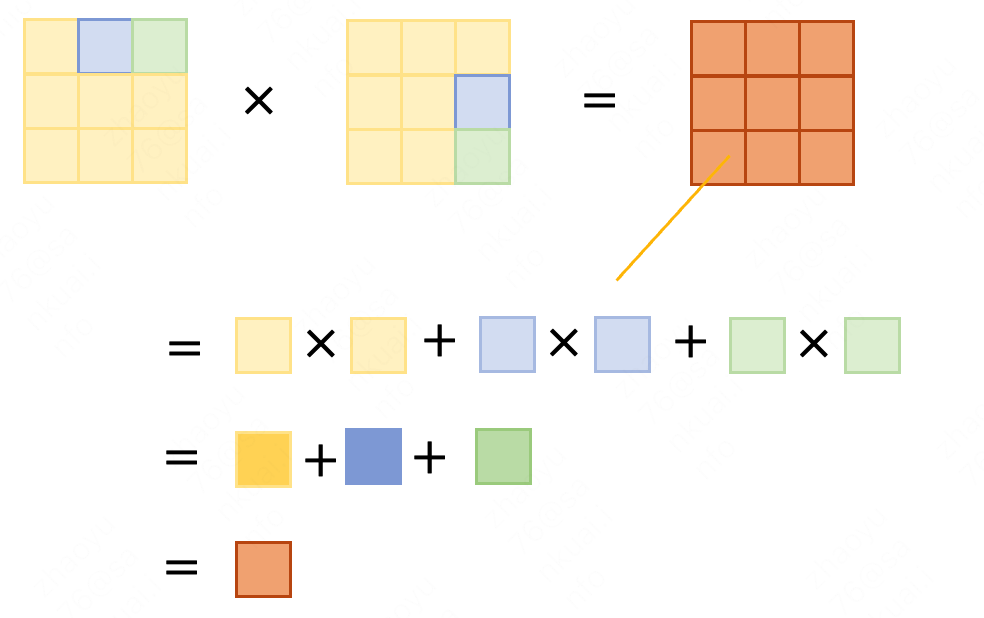
因此,如果将最后矩阵的值都缩小一定的倍数,$Softmax$激活后的梯度相对更大,模型也就更容易收敛。而这个数字如上例,就是所有元素个数开方,也既$\sqrt{9} = 3$。
多头注意力
对于attention进行scaling还可以有效的防止某些头的得分过大,同时也可以防止梯度爆炸的问题。
参数分布
我们知道模型参数初始化是尽量初始化一个方差为$1$均值为$0$的矩阵,因此大家一般都使用标准正态分布或者截尾分布(也就是约束了两端较大值的正态分布,以获得较为优秀的优化效果)来进行初始化。
而正如上文所说,经过$attention$矩阵计算后,整体参数值变大,已经没有办法保证均值,因此除以一个数后保持参数的分布。
为了保持这些参数一致性,甚至还会对一些损失函数和标准化过程进行一些更改,比如$RMS Norm$性能已经被证实优于$Layer Norm$。
0 条评论