【深度学习笔记】Bert处理超长文本

众所周知，Bert只能处理最长512长度的文本，那么如何处理超长文本呢？

我们可以使用nezha，因为它是基于相对位置编码的。

我们还可以将Bert的绝对位置编码处理一下，使其能够处理超长文本。

思路如下：

我们将超长文本映射到多层（k为文本索引），通过位置编码pos(i)和pos(j)来确定k。

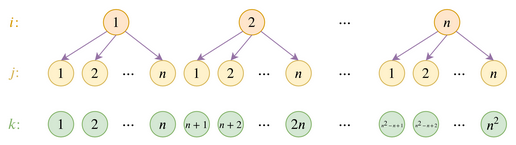
通过一个[0,1]的超参 α 来定义i和j的比例（ α ≠0.5，否则无法区分(i,j)和(j,i)）。

因此我们可以将新的位置编码设为：

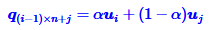
其中，u为embedding的原始数据（暂时这么理解），q为新的位置编码，(i-1)*n+j=k。

到这里比较好理解，但是我们还有个问题：

由于我们希望在长度不足512的时候，u和原始位置编码（<512）一致的，也就是说，当i=1时，q（新的embedding）和p（原始512的embedding）是相等的。因此我们可以算出u为：

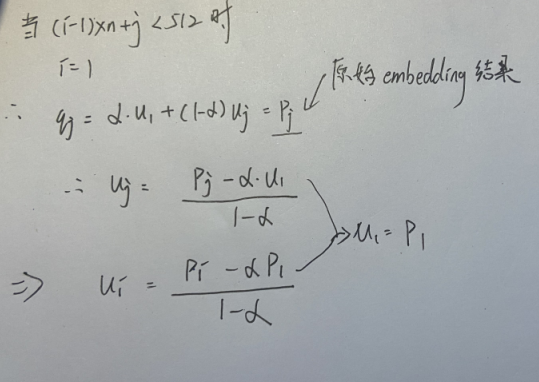
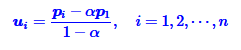
因此，当我们取u为上式时，当长度小于512和原始embedding一致。当长度大于512时，可以通过变换获得新的embedding。

具体代码实现为：

首先变换p为u：

embeddings = self.embeddings - alpha * self.embeddings[:1]
embeddings = embeddings / (1 - alpha)

随后通过u计算q：

embeddings_x = K.gather(embeddings, position_ids // self.input_dim)
embeddings_y = K.gather(embeddings, position_ids % self.input_dim)
embeddings = alpha * embeddings_x + (1 - alpha) * embeddings_y

通过实验表明， α 取0.4时效果最好。

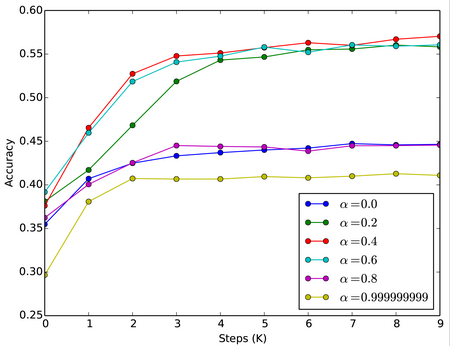
而实验效果表明，在很小的代价下，模型就能够理解这种变换，达到与之前（长度为512）相近的结果。

当然，代价也是有的，由于attention的长度增加，attention又是O(n2)的空间复杂度，因此显存占用也会有一些增加。

完整的代码：

alpha = 0.4 if self.hierarchical is True else self.hierarchical
embeddings = self.embeddings - alpha * self.embeddings[:1]
embeddings = embeddings / (1 - alpha)
embeddings_x = K.gather(embeddings, position_ids // self.input_dim)
embeddings_y = K.gather(embeddings, position_ids % self.input_dim)
embeddings = alpha * embeddings_x + (1 - alpha) * embeddings_y

感谢苏建林大佬的博客，本文为阅读原文时的笔记。