这里我们以Bert的12头注意力进行举例。
我们都知道,bert采用了12头注意力,同时每一个注意力的维度都为64。
为什么要采用64的维度而不继续采用隐藏层通用的768维度呢?
一言蔽之的话,大概是:在不增加时间复杂度的情况下,同时,借鉴CNN多核的思想,在更低的维度,在多个独立的特征空间,更容易学习到更丰富的特征信息。
知乎-海晨威
那么多头注意力是怎么做到“不增加时间复杂度”的呢?又是怎么切分多头注意力的呢?
如何切分多头注意力
首先我们重新梳理一下如何切分多头注意力机制,这里不同的框架实现的方式不同。
hugging face的transformers可能更多的是处于教学目的(因为transformers的注释真的很多)也可能是因为要保持与原文的一致性(原文就是使用的transposes and reshapes的方式),分别使用了两次reshape来完成注意力切分的工作。
而bert4keras则只是用了一次reshape。
个人感觉并没有什么实质上的差别吧
下面开始可视化的走完一遍multi head (self) attention
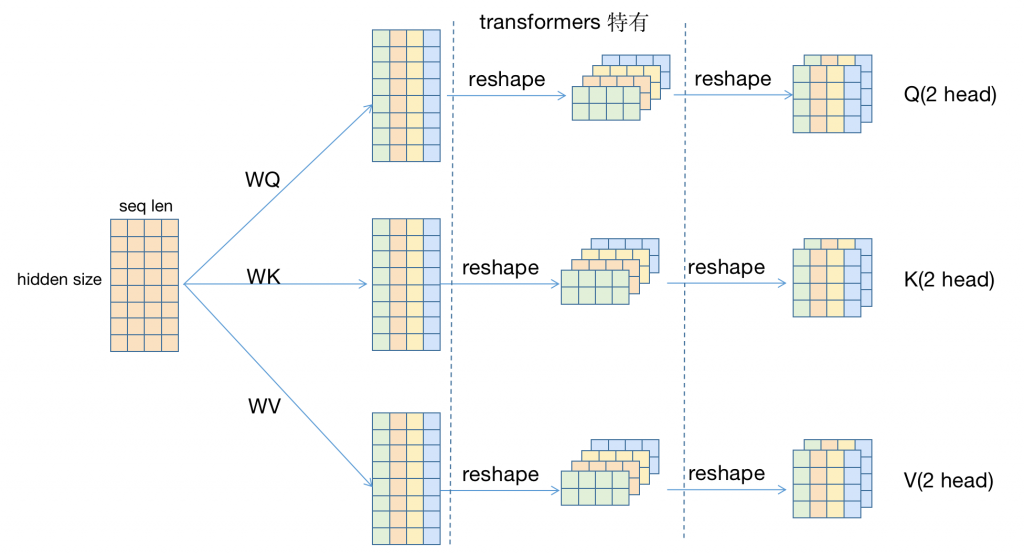
首先我们假设一个输入,该输入seq len为4,hidden size为8,使用2头注意力;同时弱化batch size(假设为1并且不在维度上体现)。
1.一个输入分别经过WQ,WK,WV得到Q,W,V三个矩阵,经过一(二)次reshape之后,得到了 3*2(qkv*head number) 个 4*4 (seq len * each head hidden size)矩阵
注意:这不是直接对输入的切分(事实上我在这里纠结了好久,甚至一度认为多头注意力的每一个头都关注原文的某一段距离),而是通过一个矩阵变换(Dense)来生成一个新的矩阵(上图中第二列)。而这些新矩阵负责将输入的隐藏层向量压缩n倍(这个n取决于使用多少头注意力),因此,虽然矩阵大小没变,但是实际的意义已经发生改变。
实际上因为属于一个变量,应该是类似于Q的堆叠形式
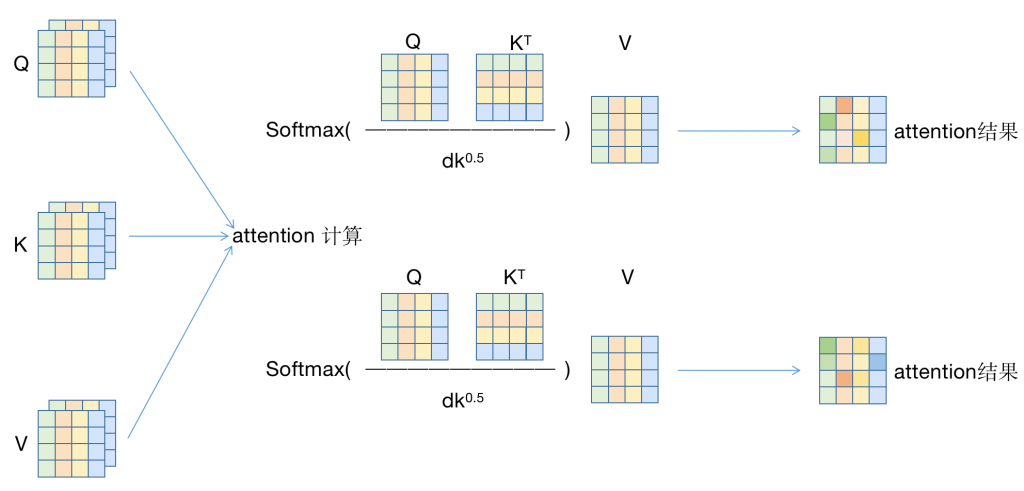
2.对于已经计算得到的QKV,分别计算attention,最终得到了attention的结果,一个2*4*4矩阵(head number * seq len * each head hidden size)
实际上因为属于一个变量,应该是类似于Q的堆叠形式
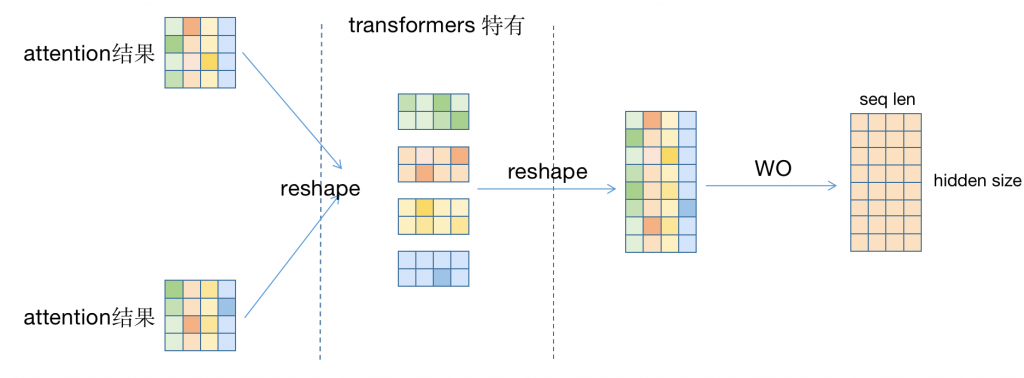
3.获取到了attention的结果后,再经过一(二)次reshape后,重新拼接回一个8*4(hidden size * seq len)矩阵。
4.得到拼接后的8*4矩阵后,经过WO,得到O矩阵,即输出。
搞清楚了如何切分多头,那么对于“为什么不增加时间复杂度”这个问题就会有一个更直观的感受了
多头注意力的时间复杂度
首先,对于多头注意力效果要优于单头注意力效果这一问题就没必要说了。
那么我们来对比一下时间复杂度吧
我们知道,self attention的时间复杂的是n^2*d,其中,n是输入序列长度,d为注意力头的隐藏层大小。
我们继续设两个变量,一个是多头注意力的头数m,一个是每一个注意力的隐藏层大小h。同时假设单头注意力的d为整个隐藏层的大小。既——对于transformer以及bert,m*h=d=768。

实际上因为属于一个变量,应该是类似于Q的堆叠形式
对于上图,实际上我们计算attention时使用的矩阵为2*4*4(其中,Q矩阵为m*n*h,K的转制矩阵为m*h*n)
计算结果为2*4*4矩阵(m*n*n)(PS突然发现例子举的不好啊,n和h一样。但是图都画完了,忍一忍,捋一捋)。
实际上这里,m*n*h与m*h*n矩阵相乘,实际上就是n*h 乘 h*n,计算m次(tf.matmul就是这么计算的),因此整体时间复杂度为m*n*n*h(m次,每一次attention的复杂度都是n^2*h)
m*n*n*h = n*n*d (m*h=d)
因此:使用这种方式进行多头注意力运算,实际时间复杂度与单头注意力的时间复杂度一样,同时增大了头数。
对于注意力头维度的降低,由于并不需要那么多维度来保存信息,并没有什么太大影响(反正作者是先跑实验再解释的,怎么解释都是对的)
2023.11.25更
最近发现一个有意思的文章。
在第二章,主要通过改变句子顺序,例如倒装等方式,判断多头注意力的权重分布。发现部分头更加注重一些语法词义的pattern。但并不是所有的头都会出现这种明显的分析,作者认为只是这个case没有用到而已,并不是这个head属于无意义head。

这里可以得到一个结论,多头attention的有些头的功能是不一样的,有的头可能没啥信息(如第5head),有的头pattern由位置信息主导,有的头由语法信息主导,有的头由词法信息主导,而能够捕捉到语法/句法/词法信息的头其实是非常少的
因此也就更需要多头注意力在降低head拟合无用信息的概率。
2 条评论
eden · 2023-03-22 16:12
Mozilla/5.0 (iPhone; CPU iPhone OS 16_3 like Mac OS X) AppleWebKit/605.1.15 (KHTML, like Gecko) Version/16.3 Mobile/15E148 Safari/604.1
谢谢!太有用了!
song · 2023-08-06 17:11
Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/115.0.0.0 Safari/537.36 Edg/115.0.1901.188
厉害