吴恩达Machine-Learning 第四周:前馈神经网络(Neural Network)
其实神经网络的性能并不是一定比逻辑回归要高。要根据数据情况选择不同的算法。
本节将针对逻辑回归和前馈神经网络对手写字的识别分别进行实现。
首先看一下 手写数字的图:
def plot_100_image(X):
"""
#绘图函数,画100张图片
X :
"""
# 获得图片大小(根号下400)
size = int(numpy.sqrt(X.shape[1]))
# 随机从X中选择100组数据
sample_idx = numpy.random.choice(numpy.arange(X.shape[0]), 100)
# 取数随机数据
sample_images = X[sample_idx, :]
fig, ax_array = plt.subplots(nrows=10, ncols=10, sharey=True, sharex=True, figsize=(8, 8))
for r in range(10):
for c in range(10):
ax_array[r, c].matshow(sample_images[10 * r + c].reshape((size, size)),
cmap=matplotlib.cm.binary)
plt.xticks(numpy.array([]))
plt.yticks(numpy.array([]))
# 随机绘制100张图片
plot_100_image(X)
plt.show()
首先是导包和基础方法:
# -*- coding:utf-8 -*-
import numpy
import scipy.optimize as opt
import scipy.io as sio
from sklearn.metrics import classification_report
"""
相关函数
"""
def read_data(filename, transpose=True):
"""
文件读取
:param filaname:
:return:
"""
data = sio.loadmat(filename)
y = data.get('y')
y = y.reshape(y.shape[0])
X = data.get('X')
if transpose:
# 转置当前数据中,可以理解为将图片旋转
X = numpy.array([im.reshape((20, 20)).T for im in X])
# 将旋转后的图片展开成一行
X = numpy.array([im.reshape(400) for im in X])
return X, y
def read_weight(filename):
"""
读取神经网络的权重
:param filename:
:return:
"""
data = sio.loadmat(filename)
return data['Theta1'], data['Theta2']
def sigmoid(x):
"""
sigmoid函数
:param x:
:return:
"""
return 1.0 / (1.0 + numpy.exp(-x))
def cost(theta, X, y):
"""
代价函数
:param theta:
:param X:
:param y:
:return:
"""
return numpy.mean(-y * numpy.log(sigmoid(X @ theta)) - (1 - y) * numpy.log(1 - sigmoid(X @ theta)))
def gradient(theta, X, y):
"""
下降函数
:param theta:
:param X:
:param y:
:return:
"""
return (1 / len(X)) * (sigmoid(X @ theta) - y) @ X
def regularized_cost(theta, X, y, l=1):
"""
正则化的代价函数
:param theta:
:param X:
:param y:
:param l:
:return:
"""
_theta = theta[1:]
reg = (1 / 2 * len(X)) * (_theta @ _theta)
return cost(theta, X, y) + reg
def regularized_gradient(theta, X, y, l=1):
"""
正则化的下降函数
:param theta:
:param X:
:param y:
:param l:
:return:
"""
reg = (1 / len(X)) * theta
reg[0] = 0
return gradient(theta, X, y) + reg
def predict(X, theta):
"""
预测函数
:param X:
:param theta:
:return:
"""
prob = sigmoid(X @ theta)
return (prob >= 0.5).astype(int)
def logistic_regression(X, y, l=1):
"""
逻辑回归函数
:param X:
:param y:
:param l:
:return:
"""
theta = numpy.zeros(X.shape[1])
result = opt.minimize(fun=regularized_cost,
x0=theta,
args=(X, y, l),
method='TNC',
jac=regularized_gradient,
options={'disp': True})
return result.x
逻辑回归的演示:
"""
逻辑回归演示
"""
raw_X, raw_y = read_data('data/ex3data1.mat')
# 处理向量
X = numpy.insert(raw_X, 0, values=numpy.ones(raw_X.shape[0]), axis=1)
y_matrix = []
for k in range(1, 11):
y_matrix.append((raw_y == k).astype(int))
# 最后一排0移到最前面
y_matrix = [y_matrix[-1]] + y_matrix[:-1]
y = numpy.array(y_matrix)
k_theta = numpy.array([logistic_regression(X, y[k]) for k in range(10)])
prob_matrix = sigmoid(X @ k_theta.T)
# 返回沿轴axis最大值的索引,axis=1代表行
y_pred = numpy.argmax(prob_matrix, axis=1)
y_answer = raw_y.copy()
y_answer[y_answer == 10] = 0
print(classification_report(y_answer, y_pred))逻辑回归的成功率:
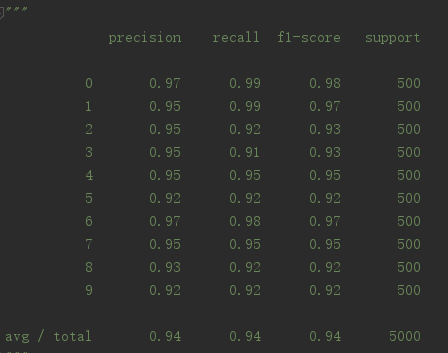
然后是神经网络,这里的神经网络使用了一个隐藏层为26个节点的隐藏层:
"""
神经网络演示
"""
theta1, theta2 = read_weight('./data/ex3weights.mat')
X, y = read_data('./data/ex3data1.mat', transpose=False)
# 第一层
l1 = X
# 对第一层添加点
l1 = numpy.insert(l1, 0, values=numpy.ones(X.shape[0]), axis=1)
# 计算第二层
l2 = sigmoid(l1 @ theta1.T)
# 对第二层添加点
l2 = numpy.insert(l2, 0, numpy.ones(l2.shape[0]), axis=1)
# 第三层
l3 = sigmoid(l2 @ theta2.T)
y_pred = numpy.argmax(l3, axis=1) + 1
print(classification_report(y, y_pred))神经网络的成功率:
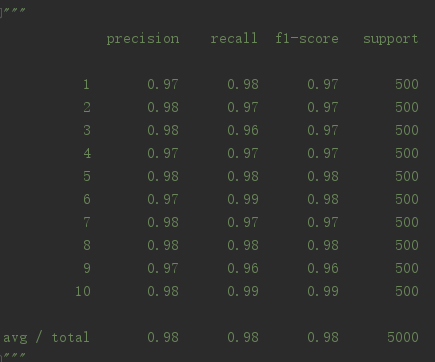
可以看到神经网络达到了98的准确率,而逻辑回归只有94,但是这并不绝对,这只能说明这组数据更适合神经网络
0 条评论