【机器学习】线性回归

于由admin发布

吴恩达Machine-Learning 第一、二周：线性回归（linear regression）

线性回归，就是在散列的数据点中寻找一条分割线，使这条分割线对于这组数据的划分最合理，也就是代价最低。

计算出当前代价后，使用梯度下降法更新theta值，以改变直线的位置也就是缩小代价，直到达到区域最优解（但不一定是全局最优解）。

首先导入相关包依赖

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

随后定义数据目录和读取数据

# 定义数据集
dataPath = './data/ex1data1.txt'
# names添加列名，header用指定的行来作为标题，若原无标题且指定标题则设为None
data = pd.read_csv(dataPath, header=None, names=["Population", 'Profit'])

画图，显示数据分布图像

# 画图
data.plot(kind='scatter', x='Population', y='Profit', figsize=(8, 5))
# 显示图像
plt.show()

我们看到，数据图像如下：

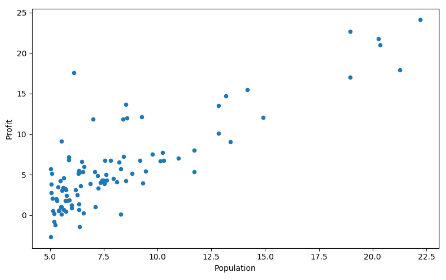
随后获取输入向量和输出向量

# 在数据中添加一个Ones列，方便我们计算代价和梯度，三个参数分别为，插入位置、插入列名、默认值
# 这样在切割掉目标向量之后输入向量依然保持在2列，方便与 未知数 矩阵相乘（因为未知数有2个）
data.insert(0, 'Ones', 1)
# 获取数据
# 获取列数
cols = data.shape[1]
# 取前cols-1列，即输入向量
x = data.iloc[:, 0:cols - 1]
# 取最后一列，即目标向量
y = data.iloc[:, cols - 1:cols]

转换数据与初始化

# 分别将两组数据转换成矩阵形式，方便运算
x = np.mat(x.values)
y = np.mat(y.values)
# 初始化theta(这个值为最终分割线的 [截距，斜率]
theta = np.mat([0, 0])

然后就可以计算代价，计算代价的方法如下

公式为

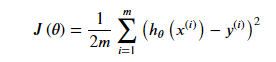
def computeCost(x, y, theta):
    """
    计算代价函数
    :param x: 输入向量
    :param y: 目标向量
    :param theta: theta
    :return:
    """
    inner = np.power(((x * theta.T) - y), 2)
    return np.sum(inner) / (2 * len(x))

调用computeCost方法

# 计算代价（32.072733877455676）
nowCost = computeCost(x, y, theta)

定义学习率和计算次数

# 学习率
alpha = 0.01
# 计算次数
epoch = 1000

然后可以进行梯度下降算法，算法如下

其中里面的公式

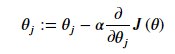
def gradientDescent(x, y, theta, alpha, epoch):
    """
    梯度下降
    :param x: x轴数据
    :param y: y轴数据
    :param theta: theta
    :param alpha: 学习率
    :param epoch:θ
    :return:
    """
    # 参数 θ的数量，用来绘制训练次数和代价的关系
    cost = np.zeros(epoch)
    # 输入数据的大小
    m = x.shape[0]
    # 进行epoch次迭代
    for i in range(epoch):
        # 利用向量化一步求解
        theta = theta - (alpha / m) * (x * theta.T - y).T * x
        # 保存当前的代价到数组中
        cost[i] = computeCost(x, y, theta)
    return theta, cost

调用梯度下降成本并调用，输出当前代价

final_theta, cost = gradientDescent(x, y, theta, alpha, epoch)
# 显示当前代价 （4.515955503078912
nowCost = computeCost(x, y, final_theta)

随后画出分割线

# 在data.Population的最大最小值范围内返回均匀间隔的数字（100个  横坐标
x = np.linspace(data.Population.min(), data.Population.max(), 100)  # 纵坐标
f = (final_theta[0, 1] * x) + final_theta[0, 0]
fig, ax = plt.subplots(figsize=(6, 4))
# 绘制直线  (横坐标  纵坐标 颜色  名字
ax.plot(x, f, 'r', label='Prediction')
# 绘制点   ( 横坐标  纵坐标  名字
ax.scatter(data['Population'], data.Profit, label='Traning Data')
# 标签显示位置  2表示在左上角
ax.legend(loc=2)
# 设置横坐标名称
ax.set_xlabel('Population')
# 设置纵坐标名称
ax.set_ylabel('Profit')
# 设置标题
ax.set_title('Predicted Profit vs. Population Size')
plt.show()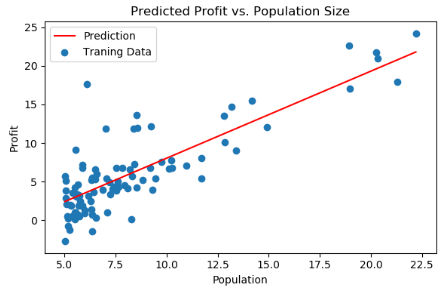

画出不同批次下的代价变化

fig, ax = plt.subplots(figsize=(8, 4))
# 绘制直线  arange 和range功能类似 均分数据
ax.plot(np.arange(epoch), cost, 'r')
# 设置横纵坐标以及图片名称
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
plt.show()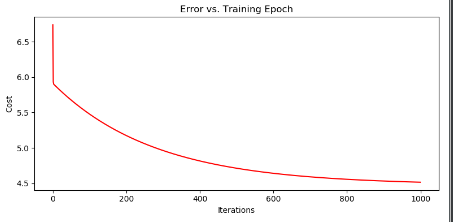

完整代码如下：

# -*- coding:utf-8 -*-
"""
线性回归，根据提示完成。
"""
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 定义数据集
dataPath = './data/ex1data1.txt'
# names添加列名，header用指定的行来作为标题，若原无标题且指定标题则设为None
data = pd.read_csv(dataPath, header=None, names=["Population", 'Profit'])
# 获取数据集的前n行数据，默认为5
# data.head()
# 计算数据集的最大值、最小值等属性值
# data.describe()
# 画图
# data.plot(kind='scatter', x='Population', y='Profit', figsize=(8, 5))
# 显示图像
# plt.show()
def computeCost(x, y, theta):
    """
    计算代价函数
    :param x: 输入向量
    :param y: 目标向量
    :param theta: theta
    :return:
    """
    inner = np.power(((x * theta.T) - y), 2)
    return np.sum(inner) / (2 * len(x))
# 在数据中添加一个Ones列，方便我们计算代价和梯度，三个参数分别为，插入位置、插入列名、默认值
# 这样在切割掉目标向量之后输入向量依然保持在2列，方便与 未知数 矩阵相乘（因为未知数有2个）
data.insert(0, 'Ones', 1)
# 获取数据
# 获取列数
cols = data.shape[1]
# 取前cols-1列，即输入向量
x = data.iloc[:, 0:cols - 1]
# 取最后一列，即目标向量
y = data.iloc[:, cols - 1:cols]
# 分别将两组数据转换成矩阵形式，方便运算
x = np.mat(x.values)
y = np.mat(y.values)
# 初始化theta(这个值为最终分割线的 [截距，斜率]
theta = np.mat([0, 0])
# 计算代价（32.072733877455676）
nowCost = computeCost(x, y, theta)
def gradientDescent(x, y, theta, alpha, epoch):
    """
    梯度下降
    :param x: x轴数据
    :param y: y轴数据
    :param theta: theta
    :param alpha: 学习率
    :param epoch:θ
    :return:
    """
    # 参数 θ的数量，用来绘制训练次数和代价的关系
    cost = np.zeros(epoch)
    # 输入数据的大小
    m = x.shape[0]
    # 进行epoch次迭代
    for i in range(epoch):
        # 利用向量化一步求解
        theta = theta - (alpha / m) * (x * theta.T - y).T * x
        # 保存当前的代价到数组中
        cost[i] = computeCost(x, y, theta)
    return theta, cost
# 学习率
alpha = 0.01
# 计算次数
epoch = 1000
final_theta, cost = gradientDescent(x, y, theta, alpha, epoch)
# 显示当前代价 （4.515955503078912
nowCost = computeCost(x, y, final_theta)
# 在data.Population的最大最小值范围内返回均匀间隔的数字（100个   横坐标
x = np.linspace(data.Population.min(), data.Population.max(), 100)  # 纵坐标
f = (final_theta[0, 1] * x) + final_theta[0, 0]
fig, ax = plt.subplots(figsize=(6, 4))
# 绘制直线  (横坐标  纵坐标 颜色  名字
ax.plot(x, f, 'r', label='Prediction')
# 绘制点   ( 横坐标  纵坐标  名字
ax.scatter(data['Population'], data.Profit, label='Traning Data')
# 标签显示位置  2表示在左上角
ax.legend(loc=2)
# 设置横坐标名称
ax.set_xlabel('Population')
# 设置纵坐标名称
ax.set_ylabel('Profit')
# 设置标题
ax.set_title('Predicted Profit vs. Population Size')
plt.show()
fig, ax = plt.subplots(figsize=(8, 4))
# 绘制直线  arange 和range功能类似 均分数据
ax.plot(np.arange(epoch), cost, 'r')
# 设置横纵坐标以及图片名称
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
plt.show()

下面是选修作业，多了对数据进行标准化操作，这一步是将很大的数据映射到一个很小的范围并且保留数据的特征，并且防止了梯度爆炸

# -*- coding:utf-8 -*-
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
data = pd.read_csv("./data/ex1data2.txt", names=['Size', 'Bedrooms', 'Price'])
plt.show()
# 进行归一化特征 mean 获取平均值  std获取标准差
# 这一步是将很大的数据映射到一个很小的范围并且保留数据的特征，防止了梯度爆炸
data = (data - data.mean()) / data.std()
# 首先进行数据划分，增肌Ones列
data.insert(0, "Ones", 1)
# 获取列数
cols = data.shape[1]
# 分割输入向量并转换为矩阵
inputVector = data.iloc[:, 0:cols - 1]
inputVector = np.mat(inputVector)
# 获取目标向量并转换为矩阵
aimVector = data.iloc[:, cols - 1:cols]
aimVector = np.mat(aimVector)
# 定义theta
theta = np.mat([0, 0, 0])
def computeCost(inputVector, aimVector, theta):
    """
    计算代价函数
    :param inputVector: 输入向量
    :param aimVector: 目标向量
    :param theta: theta
    :return:
    """
    inner = np.power(((inputVector * theta.T) - aimVector), 2)
    return np.sum(inner) / (2 * len(inputVector))
# 当前代价 （0.48936170212765967
nowCost = computeCost(inputVector, aimVector, theta)
# 定义学习率
alpha = 0.01
# 定义迭代次数
epoch = 1000
def gradientDescent(inputVector, aimVector, theta, alpha, epoch):
    # 代价数组，记录代价变化
    cost = np.zeros(epoch)
    length = len(inputVector)
    for i in range(epoch):
        theta = theta - (alpha / length) * ((inputVector * theta.T) - aimVector).T * inputVector
        cost[i] = computeCost(inputVector, aimVector, theta)
    return theta, cost
finalTheta, costList = gradientDescent(inputVector, aimVector, theta, alpha, epoch)
# 当前的代价 （0.13070336960771892
nowCost = computeCost(inputVector, aimVector, finalTheta)
# 绘制代价变化图
fig, ax = plt.subplots()
ax.plot(np.arange(epoch), costList, 'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
plt.show()
# 使用正规方程来计算theta
def normalEqn(X, y):
    theta = np.linalg.inv(X.T @ X) @ X.T @ y
    return theta
finalTheta2 = normalEqn(inputVector, aimVector)  # 感觉和批量梯度下降的theta的值有点差距

在最后还需要提到标准方程

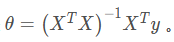
该方程可以得到和梯度下降一样的结果

实现代码如下

# 使用正规方程来计算theta
def normalEqn(X, y):
    theta = np.linalg.inv(X.T @ X) @ X.T @ y
    return theta

这种方法可以不使用梯度下降而得到theta值，两种方法的优缺点如下

正规方程不需要指定学习率和迭代次数，减少了参数也随之降低了难度。但是正规方程的时间复杂度为O(n³)，复杂度较高，所以在高数量级的数据集中使用正规方程并不是一个好主意。

分类： 机器学习实战算法

0 条评论

发表回复

Avatar placeholder

您的电子邮箱地址不会被公开。

相关文章

算法

【Leetcode】排序集锦

L215：数组中的第K个最大元素 https://leetcode-c 阅读更多…

算法

【LeetCode】双指针集锦

啊，要找工作了，耽误了好久的刷题重新捡起来。 不再按顺序刷题了（有时间 阅读更多…

算法

【LeetCode】*0287 寻找重复数

https://leetcode-cn.com/problems/fi 阅读更多…