吴恩达Machine-Learning 第三周:逻辑回归(logistic regression)
逻辑回归和线性回归,本质上是一样的,只不过一个使用平方代价函数同来预测值,一个使用log代价函数用来进行分类。
首先一样是导包:
import numpy
import pandas
import matplotlib.pyplot as plt
import scipy.optimize as opt
from sklearn.metrics import classification_report然后是画图查看原始数据:
data = pandas.read_csv('./data/ex2data1.txt', header=None, names=['exam1', 'exam2', 'admitted'])
# 查看数据样式
fig, ax = plt.subplots()
positive = data[data.admitted.isin(['1'])] # 1
negative = data[data.admitted.isin(['0'])] # 0
ax.scatter(positive['exam1'], positive['exam2'], c='b', marker='v', label='Admitted')
ax.scatter(negative['exam1'], negative['exam2'], c='r', marker='x', label='Not Admitted')
# 设置横纵坐标名
ax.set_xlabel('Exam 1 Score')
ax.set_ylabel('Exam 2 Score')
plt.show()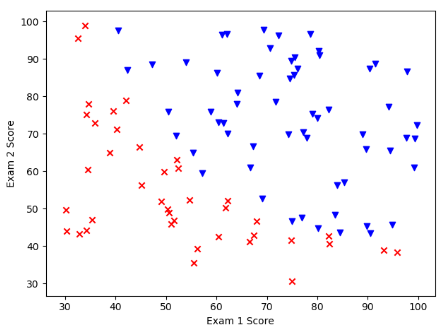
然后是sigmoid和代价计算函数:
def sigmoid(z):
"""
定义sigmoid函数
:param z: 原函数
:return: 变换后的函数
"""
return 1.0 / (1 + numpy.exp(-z))
def computeCost(theta, X, y):
"""
计算代价
:param X: 输入数据
:param y:目标数据
:param theta: theta
:return:计算后的代价
"""
# X.T@X等价于X.T.dot(X)
return numpy.mean(-y * numpy.log(sigmoid(X @ theta)) - (1 - y) * numpy.log(1 - sigmoid(X @ theta)))
然后是标准化数据,增加Ones列:
# 插入一行数据,方便运算
data.insert(0, 'Ones', 1)
# 输入、目标向量初始化,这里没有像之前一样转换成矩阵,因为梯度下降可以向量化计算
X = data.iloc[:, :-1].values
y = data.iloc[:, -1].values
theta = numpy.zeros(X.shape[1])
# 计算代价 (0.6931471805599453
print(computeCost(theta, X, y))
梯度下降:
def gradientDescent(theta, X, y):
"""
梯度下降计算
:param X: 输入向量
:param y: 目标向量
:param theta: theta
:return: theta
"""
for i in range(10000):
theta = theta - 0.01 * (X.T @ (sigmoid(X @ theta) - y)) / len(X)
return theta
"""
这的坑也太大了,网上很多版本(黄博github里的也是, 都是在梯度下降里不使用循环,只有一次
这里他们只是演示梯度下降过程,实际上是需要循环的
他们后面的测试和绘图都是使用后面的scipy方法所计算出的数据来计算,因此这里不循环返回的“劣质”结果对后面没影响
同时,梯度下降的循环调用由scipy进行,不需要在方法内进行循环
"""
# [-7.65900397 0.41024768 -0.05324509]
print(gradientDescent(theta, X, y))
def gradient(theta, X, y):
"""
这个是没有循环的版本,由scipy来调用
:param theta:
:param X:
:param y:
:return:
"""
return (1 / len(X)) * X.T @ (sigmoid(X @ theta) - y)使用sklearn来计算:
# 使用sklearn计算
"""
a) liblinear:使用了开源的liblinear库实现,内部使用了坐标轴下降法来迭代优化损失函数。
b) lbfgs:拟牛顿法的一种,利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
c) newton-cg:也是牛顿法家族的一种,利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
d) sag:即随机平均梯度下降,是梯度下降法的变种,和普通梯度下降法的区别是每次迭代仅仅用一部分的样本来计算梯度,
适合于样本数据多的时候。
"""
print(numpy.shape(X))
print(numpy.shape(y))
print(numpy.shape(theta))
res = opt.minimize(fun=computeCost, x0=theta, args=(X, y), method='Newton-CG', jac=gradient)
# [-25.16143003, 0.20623248, 0.20147238]
print(res)执行预测:
def predict(x, theta):
"""
预测函数
:param x:
:param theta:
:return:
"""
prob = sigmoid(x @ theta)
return (prob >= 0.5).astype(int)
# 查看计算出的参数在训练集上的表现
final_theta = res.x
y_pred = predict(X, final_theta)
"""
precision recall f1-score support
0 0.87 0.85 0.86 40
1 0.90 0.92 0.91 60
accuracy 0.89 100
macro avg 0.89 0.88 0.88 100
"""
print(classification_report(y, y_pred))寻找决策边界与画图:
# 寻找决策边界
"""
这里这么操作是将计算出的参数转化成y=ax+b的格式,将最后一位设法取成-1,再移到等式的另一侧即为y=ax+b 格式
"""
coef = -(res.x / res.x[2])
print(coef)
x = numpy.linspace(data['exam1'].min(), data['exam1'].max(), 100)
y = coef[0] + coef[1] * x
fig, ax = plt.subplots()
positive = data[data.admitted.isin(['1'])] # 1
negative = data[data.admitted.isin(['0'])] # 0
ax.scatter(positive['exam1'], positive['exam2'], c='b', marker='v', label='Admitted')
ax.scatter(negative['exam1'], negative['exam2'], c='r', marker='x', label='Not Admitted')
# 设置横纵坐标名
ax.set_xlabel('Exam 1 Score')
ax.set_ylabel('Exam 2 Score')
# 绘制分割线
plt.plot(x, y, 'r')
plt.legend(loc=2)
plt.show()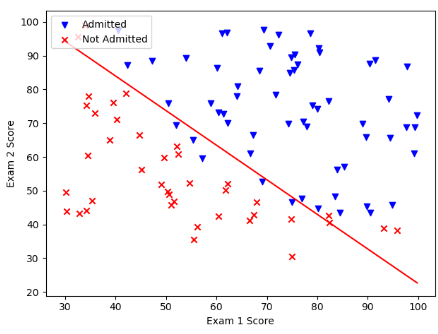
0 条评论