吴恩达Machine-Learning 第七周:支持向量机(support vector machine)
1.线性支持向量机
对于线性支持向量机,和逻辑回归十分类似,不同的是,代价函数发生变化。
由:
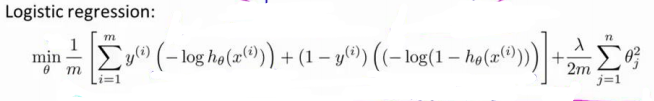
变成:
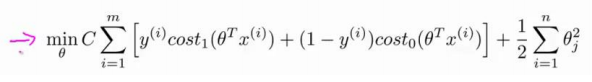
这里将代价函数图形变为:
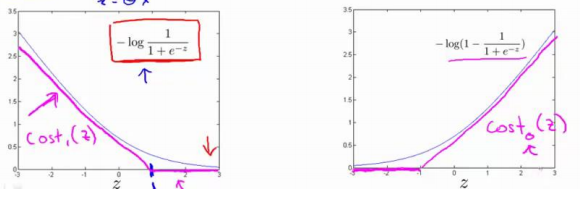
这样代价计算就从之前的>0和<0的分界变成<-1和>1。那么出错的概率也就更低。
同时对于前面的常数C,如下图,两个分界线很明显黑线要比紫色的分类效果要好,而C就是决定这条线的。
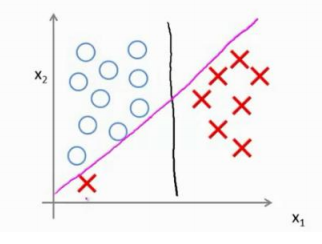
如果你将 C 设置的不要太大,则你最终会得到这条黑线 ,当 C 不是非常非常大的时候,它可以忽略掉一些异常点的 影响,得到更好的决策界。
下面使用代码画图验证:
首先导包:
import numpy as np
import pandas as pd
import sklearn.svm
import seaborn as sns
import scipy.io as sio
import matplotlib.pyplot as plt读取数据:
mat = sio.loadmat('./data/ex6data1.mat')
print(mat.keys())
data = pd.DataFrame(mat.get('X'), columns=['X1', 'X2'])
data['y'] = mat.get('y')查看数据:
fig, ax = plt.subplots(figsize=(8, 6))
ax.scatter(data['X1'], data['X2'], s=50, c=data['y'])
ax.set_title('Raw data')
ax.set_xlabel('X1')
ax.set_ylabel('X2')
plt.show()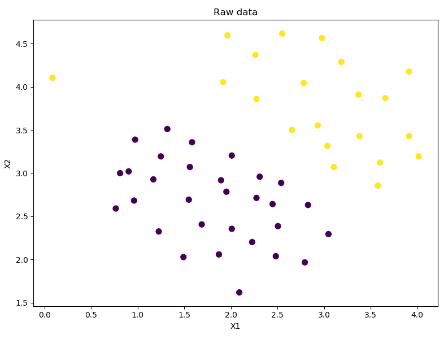
当C=1时,使用支持向量机进行计算并画图:
svc1 = sklearn.svm.LinearSVC(C=1, loss='hinge')
svc1.fit(data[['X1', 'X2']], data['y'])
svc1.score(data[['X1', 'X2']], data['y'])
data['SVM1 Confidence'] = svc1.decision_function(data[['X1', 'X2']])
fig, ax = plt.subplots(figsize=(8, 6))
ax.scatter(data['X1'], data['X2'], s=50, c=data['SVM1 Confidence'])
ax.set_title('SVM (C=1) Decision Confidence')
plt.show()其中sklearn.svm.LinearSVC中用到的参数说明如下:
"""
C : float, optional (default=1.0)
Penalty parameter C of the error term.
loss : string, ‘hinge’ or ‘squared_hinge’ (default=’squared_hinge’)
Specifies the loss function. ‘hinge’ is the standard SVM loss (used e.g. by the SVC class) while ‘squared_hinge’ is the square of the hinge loss.
"""图像如下,注意看这个点,被划分为左下类别了。同时我们差不多可以画出它分类的这条线了。
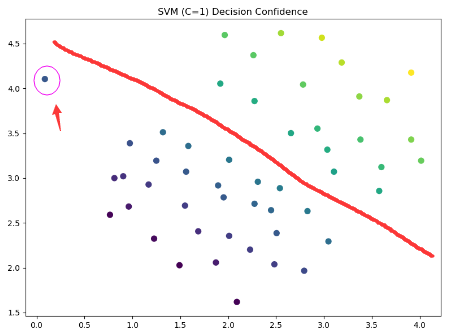
当C变成100时:
svc100 = sklearn.svm.LinearSVC(C=100, loss='hinge')
svc100.fit(data[['X1', 'X2']], data['y'])
svc100.score(data[['X1', 'X2']], data['y'])
data['SVM100 Confidence'] = svc100.decision_function(data[['X1', 'X2']])
fig, ax = plt.subplots(figsize=(8, 6))
ax.scatter(data['X1'], data['X2'], s=50, c=data['SVM100 Confidence'])
ax.set_title('SVM (C=100) Decision Confidence')
plt.show()这时可能的分界线就是这样的:
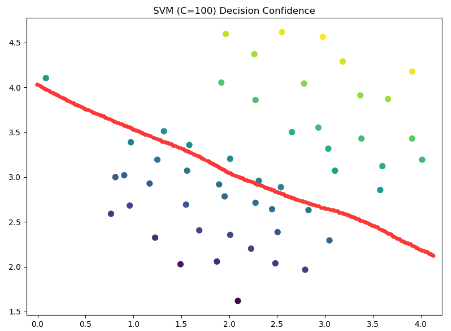
2.使用高斯核函数的支持向量机
核函数其实就是将二维的数据提升多多维,这样可以找到非线性的数据分类边界,类似于这样。
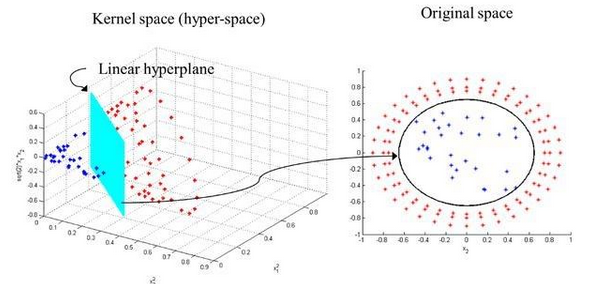
高斯函数如下:
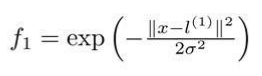
对于不同的参数,图也会产生不一样的效果。
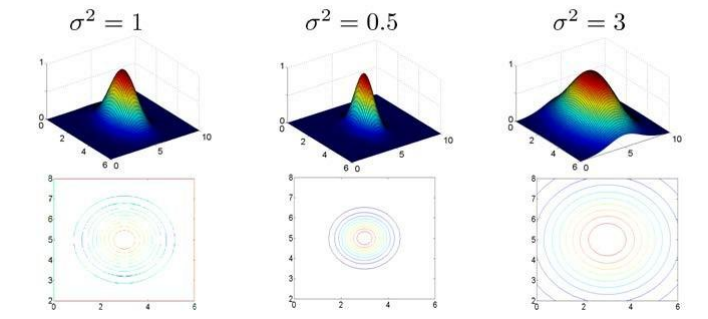
下面是支持向量机的两个参数 C 和 σ 的影响:
- C=1/λ C 较大时,相当于 λ 较小,可能会导致过拟合,高方差;
- C 较小时,相当于 λ 较大,可能会导致低拟合,高偏差;
- σ 较大时,可能会导致低方差,高偏差;
- σ 较小时,可能会导致低偏差,高方差。
下面我们使用一下使用高斯函数的支持向量机:
首先导包:
import matplotlib.pyplot as plt
from sklearn import svm
import numpy as np
import pandas as pd
import seaborn as sns
import scipy.io as sio读取数据并画出数据图像:
mat = sio.loadmat('./data/ex6data2.mat')
print(mat.keys())
data = pd.DataFrame(mat.get('X'), columns=['X1', 'X2'])
data['y'] = mat.get('y')
sns.lmplot('X1', 'X2', hue='y', data=data,
height=5,
fit_reg=False,
scatter_kws={"s": 10})
plt.show()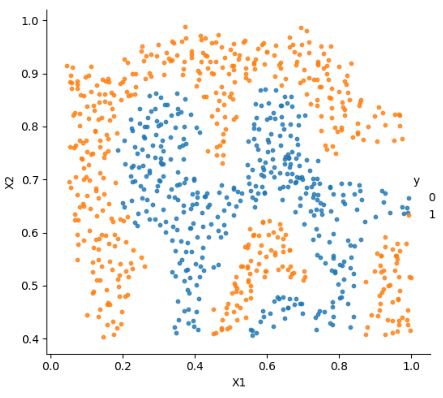
随后是使用支持向量机进行的分类:
svc = svm.SVC(C=100, kernel='rbf', gamma=10, probability=True)
print(svc)
svc.fit(data[['X1', 'X2']], data['y'])
svc.score(data[['X1', 'X2']], data['y'])
predict_prob = svc.predict_proba(data[['X1', 'X2']])[:, 0]
fig, ax = plt.subplots(figsize=(8,6))
ax.scatter(data['X1'], data['X2'], s=30, c=predict_prob)
plt.show()其中svm中部分参数如下:
"""
线性核函数kernel='linear'
多项式核函数kernel='poly'
径向基核函数kernel='rbf'
sigmod核函数kernel='sigmod'
"""最终画出来的图,可以看到和用结果画的数据图差不太多:
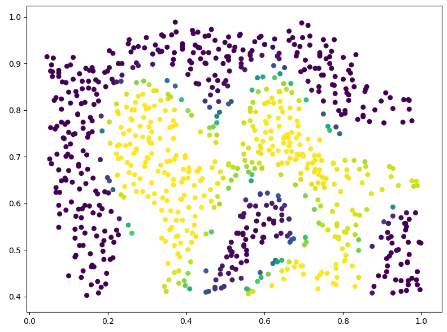
0 条评论