吴恩达机器学习第八周:K-means与PCA(K-means and PCA)。

1.使用K-means进行簇分类
K-means,聚类算法,通过寻找最接近分类中心的点来寻找分类中心。
首先导包:
import numpy as np
import matplotlib.pyplot as plt
from scipy.io import loadmat将点分类(依据现有分类中心点 ):
def findClosestCentroids(X, centroids):
"""
output a one-dimensional array idx that holds the
index of the closest centroid to every training example.
输出一个一维数组idx,其中包含最接近每个分类的中心的点集合。
:param X: 数据点
:param centroids: 分类中心点
:return:
"""
idx = []
max_dist = 1000000 # 限制一下最大距离
for i in range(len(X)):
minus = X[i] - centroids # 该点与三个分类中心的距离
dist = minus[:, 0] ** 2 + minus[:, 1] ** 2 # 计算欧几里德距离
if dist.min() < max_dist: # 限制最大距离
ci = np.argmin(dist) # 寻找最小距离的点
idx.append(ci)
return np.array(idx)读取数据,设定三个中心点,分类数据:
mat = loadmat('data/ex7data2.mat')
# print(mat.keys())
X = mat['X']
init_centroids = np.array([[3, 3], [6, 2], [8, 5]])
idx = findClosestCentroids(X, init_centroids)
# [0 2 1]
print(idx[0:3])计算新的分类中心点:
def computeCentroids(X, idx):
"""
计算新的分类中心点
:param X: 数据点
:param idx: 分类的一维数组
:return:
"""
centroids = []
for i in range(len(np.unique(idx))): # 遍历每一个k
u_k = X[idx == i].mean(axis=0) # 求每列的平均值
centroids.append(u_k)
return np.array(centroids)打印结果:
"""
[[2.42830111 3.15792418]
[5.81350331 2.63365645]
[7.11938687 3.6166844 ]]
"""
print(computeCentroids(X, idx))画图:
def plotData(X, centroids, idx=None):
"""
可视化数据,并自动分开着色。
:param X: 原始数据
:param centroids: 包含每次中心点历史记录
:param idx: 最后一次迭代生成的idx向量,存储每个样本分配的簇中心点的值
:return:
"""
# 颜色列表
colors = ['b', 'g', 'gold', 'darkorange', 'salmon', 'olivedrab', 'maroon', 'navy', 'sienna', 'tomato', 'lightgray',
'gainsboro', 'coral', 'aliceblue', 'dimgray', 'mintcream', 'mintcream']
# 断言,如果条件为真就正常运行,条件为假就出发异常
assert len(centroids[0]) <= len(colors), 'colors not enough '
subX = [] # 分号类的样本点
if idx is not None:
for i in range(centroids[0].shape[0]):
x_i = X[idx == i]
subX.append(x_i)
else:
subX = [X] # 将X转化为一个元素的列表,每个元素为每个簇的样本集,方便下方绘图
# 分别画出每个簇的点,并着不同的颜色
plt.figure(figsize=(8, 5))
for i in range(len(subX)):
xx = subX[i]
plt.scatter(xx[:, 0], xx[:, 1], c=colors[i], label='Cluster %d' % i)
plt.legend()
plt.grid(True)
plt.xlabel('x1', fontsize=14)
plt.ylabel('x2', fontsize=14)
plt.title('Plot of X Points', fontsize=16)
# 画出簇中心点的移动轨迹
xx, yy = [], []
for centroid in centroids:
xx.append(centroid[:, 0])
yy.append(centroid[:, 1])
plt.plot(xx, yy, 'rx--', markersize=8)
plt.show()
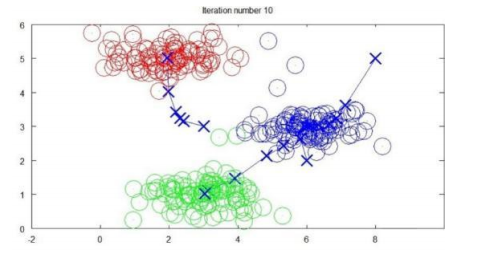
plotData(X, [init_centroids])可以看到我们初始化的三个分类中心点:
然后执行K-means算法:
def runKmeans(X, centroids, max_iters):
"""
执行k-均值算法
:param X: 原始数据
:param centroids: 中心点
:param max_iters:最大迭代次数
:return:
"""
# k ,虽然没啥用
K = len(centroids)
# 所有的点(多次迭代)
centroids_all = []
centroids_all.append(centroids)
centroid_i = centroids
for i in range(max_iters):
idx = findClosestCentroids(X, centroid_i)
centroid_i = computeCentroids(X, idx)
centroids_all.append(centroid_i)
return idx, centroids_all
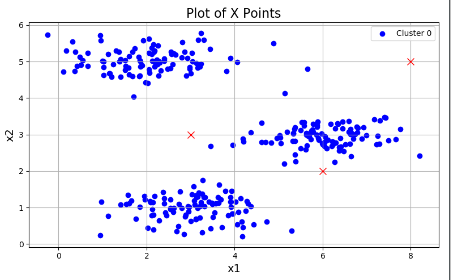
idx, centroids_all = runKmeans(X, init_centroids, 20)
plotData(X, centroids_all, idx)分类结果以及分类中心点变化的过程:
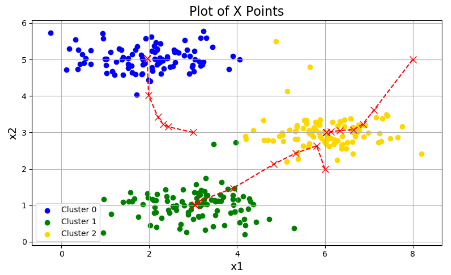
下面是随机初始化和进行三次的结果:
def initCentroids(X, K):
"""
随机初始化
:param X:
:param K:
:return:
"""
m, n = X.shape
idx = np.random.choice(m, K) # 随机从m中选择k个
centroids = X[idx]
return centroids
# 随机寻找三个随机初始中心
for i in range(3):
centroids = initCentroids(X, 3)
idx, centroids_all = runKmeans(X, centroids, 10)
plotData(X, centroids_all, idx)三张图分别为:

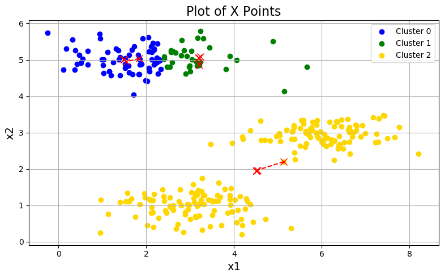
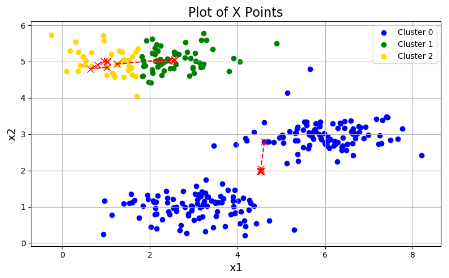
可以看出效果参差不齐,这是因为初始的分类中心点的选择不同,导致结果不同。
整理后的代码:
# -*- coding:utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
import scipy.io as sio
def loadData():
"""
读取数据
:return:
"""
mat = sio.loadmat('data/ex7data2.mat')
X = mat['X']
return X, mat
def findClosestControids(X, centroids):
"""
寻找里分类中心点最近的点集合
:param X: 原始数据
:param centroids: 分类中心点
:return: 分类结果组成的一维数组
"""
idx = []
max_distance = 1000000 # 最大距离
for i in range(len(X)):
# 该点和各个点的距离
distances = X[i] - centroids
# 计算欧几里德距离
euclid_distance = distances[:,0] ** 2 + distances[:,1] ** 2
if euclid_distance.min() < max_distance:
ci = np.argmin(euclid_distance)
idx.append(ci)
return np.array(idx)
def computeCentroids(X, idx):
"""
计算分类中心
:param X: 原始数据
:param idx: 一维分类结果数组
:return: 计算后的中心点
"""
centroids = []
for i in range(len(np.unique(idx))):
# 计算每一列的平均值
u_k = X[idx == i].mean(axis=0)
centroids.append(u_k)
return np.array(centroids)
def runKmeans(X, centroids, max_iters):
"""
k均值算法,
:param X: 原始数据
:param centroids: 中心点
:param max_iters: 最大迭代次数
:return: 执行后的分类结果以及中心点变化轨迹
"""
centroid_all = []
centroid_all.append(centroids)
idx = []
for i in range(max_iters):
idx = findClosestControids(X, centroids)
centroid_i = computeCentroids(X, idx)
centroid_all.append(centroid_i)
return idx, centroid_all
def initCentroids(X, K):
"""
随机初始化类中心点
:param X: 原始数据
:param K: 分k
:return: 找到的中心点
"""
m, n = np.shape(X)
centroid_index = np.random.choice(m, K)
centroids = X[centroid_index]
return centroids
def plotData(X, centroids, idx=None):
"""
可视化数据,并自动分开着色。
:param X: 原始数据
:param centroids: 包含每次中心点历史记录
:param idx: 最后一次迭代生成的idx向量,存储每个样本分配的簇中心点的值
:return:
"""
# 颜色列表
colors = ['b', 'g', 'gold', 'darkorange', 'salmon', 'olivedrab', 'maroon', 'navy', 'sienna', 'tomato', 'lightgray',
'gainsboro', 'coral', 'aliceblue', 'dimgray', 'mintcream', 'mintcream']
# 断言,如果条件为真就正常运行,条件为假就出发异常
assert len(centroids[0]) <= len(colors), 'colors not enough '
subX = [] # 分号类的样本点
if idx is not None:
for i in range(centroids[0].shape[0]):
x_i = X[idx == i]
subX.append(x_i)
else:
subX = [X] # 将X转化为一个元素的列表,每个元素为每个簇的样本集,方便下方绘图
# 分别画出每个簇的点,并着不同的颜色
plt.figure(figsize=(8, 5))
for i in range(len(subX)):
xx = subX[i]
plt.scatter(xx[:, 0], xx[:, 1], c=colors[i], label='Cluster %d' % i)
plt.legend()
plt.grid(True)
plt.xlabel('x1', fontsize=14)
plt.ylabel('x2', fontsize=14)
plt.title('Plot of X Points', fontsize=16)
# 画出簇中心点的移动轨迹
xx, yy = [], []
for centroid in centroids:
xx.append(centroid[:, 0])
yy.append(centroid[:, 1])
plt.plot(xx, yy, 'rx--', markersize=8)
plt.show()
if __name__ == '__main__':
# 读取数据
X, _ = loadData()
# 执行三次
for i in range(3):
# 随机初始化
centroids = initCentroids(X, 3)
idx, centroids_all = runKmeans(X, centroids, 10)
plotData(X, centroids_all, idx)
pass
2.使用K-means进行图像压缩(通过减少图像中出现的颜色的数量 )
首先导包:
from skimage import io
import numpy as np
import matplotlib.pyplot as plt
读取数据并查看图像:
A = io.imread('data/bird_small.png')
# (128, 128, 3)
print(A.shape)
plt.imshow(A)
plt.show()

然后就是和上面一样的中心点初始化、中心点计算和分类计算:
def initCentroids(X, K):
"""随机初始化"""
m, n = X.shape
idx = np.random.choice(m, K)
centroids = X[idx]
return centroids
def runKmeans(X, centroids, max_iters):
K = len(centroids)
centroids_all = []
centroids_all.append(centroids)
centroid_i = centroids
for i in range(max_iters):
idx = findClosestCentroids(X, centroid_i)
centroid_i = computeCentroids(X, idx)
centroids_all.append(centroid_i)
return idx, centroids_all
def findClosestCentroids(X, centroids):
"""
output a one-dimensional array idx that holds the
index of the closest centroid to every training example.
"""
idx = []
max_dist = 1000000 # 限制一下最大距离
for i in range(len(X)):
minus = X[i] - centroids # here use numpy's broadcasting
dist = minus[:, 0] ** 2 + minus[:, 1] ** 2
if dist.min() < max_dist:
ci = np.argmin(dist)
idx.append(ci)
return np.array(idx)
def computeCentroids(X, idx):
centroids = []
for i in range(len(np.unique(idx))): # np.unique() means K
u_k = X[idx == i].mean(axis=0) # 求每列的平均值
centroids.append(u_k)
return np.array(centroids)
最后查看操作后的图片:
X = A.reshape(-1, 3)
K = 16
centroids = initCentroids(X, K)
idx, centroids_all = runKmeans(X, centroids, 10)
img = np.zeros(X.shape)
centroids = centroids_all[-1]
for i in range(len(centroids)):
img[idx == i] = centroids[i]
img = img.reshape((128, 128, 3))
fig, axes = plt.subplots(1, 2, figsize=(12, 6))
axes[0].imshow(A)
axes[1].imshow(img)
plt.show()

可以看到图片的样子基本被保留,但是压缩后的图片只有16种颜色。
整理后的代码:
# -*- coding:utf-8 -*-
import numpy as np
from skimage import io
import matplotlib.pyplot as plt
def loadData():
"""
读取数据
:return:
"""
mig = io.imread('data/bird_small.png')
plt.imshow(mig)
return mig / 255.
def initcentroids(X, K):
"""
随机初始化分类中心点
:param X:
:param K:
:return:
"""
m, n = np.shape(X)
idx = np.random.choice(m, K)
return X[idx]
def findClosestCentroids(X, centroids):
"""
依据分类中心点划分数据点
:param X:
:param centroids:
:return:
"""
idx = []
max_distance = 100000
for i in range(len(X)):
distance = X[i] - centroids
euclid_distance = distance[:, 0] ** 2 + distance[:, 1] ** 2
if euclid_distance.min() < max_distance:
ci = np.argmin(euclid_distance)
idx.append(ci)
return np.array(idx)
def computeCentroids(X, idx):
"""
计算新的中心分类点
:param X:
:param centroids:
:return:
"""
centroids = []
for i in range(len(np.unique(idx))):
u_k = X[idx == i].mean(axis=0)
centroids.append(u_k)
return np.array(centroids)
def runKMeans(X, K, max_iters):
"""
执行k 均值算法
:param X:
:param K:
:param max_iters:
:return:
"""
centroids = initcentroids(X, K)
centroids_all = []
centroids_all.append(centroids)
for i in range(max_iters):
idx = findClosestCentroids(X, centroids)
centroids_i = computeCentroids(X, idx)
centroids_all.append(centroids_i)
return idx, centroids_all
if __name__ == '__main__':
A = loadData()
X = A.reshape(-1, 3)
idx, centroids_all = runKMeans(X, 16, 10)
img = np.zeros(X.shape)
centroids = centroids_all[-1]
for i in range(len(centroids)):
img[idx == i] = centroids[i]
img = img.reshape((128, 128, 3))
fig, axes = plt.subplots(1, 2, figsize=(12, 6))
axes[0].imshow(A)
axes[1].imshow(img)
plt.show()
在K-means中,对于K尝尝使用肘型图进行判断:
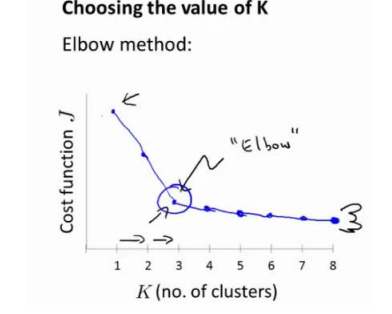
但是这个图一般情况下并不会有这么清楚地拐点,因此还需要根据实际情况进行判断。
3.使用PCA将2D数据降维到1D
首先导包:
import numpy as np import matplotlib.pyplot as plt from scipy.io import loadmat
读取数据并查看原始数据:
mat = loadmat('data/ex7data1.mat')
X = mat['X']
# (50, 2)
print(X.shape)
plt.scatter(X[:, 0], X[:, 1], facecolors='none', edgecolors='b')
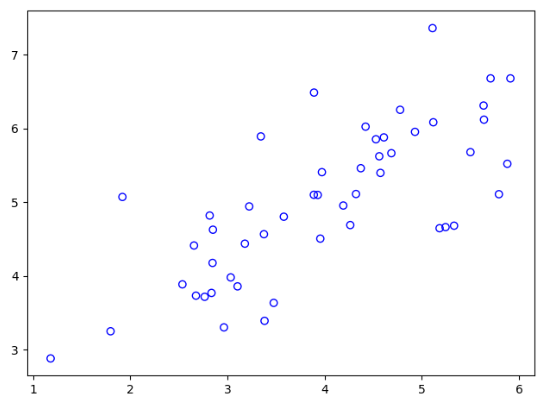
然后是数据的标准化(防止过拟合):
def featureNormalize(X):
"""
数据标准化
:param X:
:return:
"""
means = X.mean(axis=0)
stds = X.std(axis=0)
X_norm = (X - means) / stds
return X_norm, means, stds
计算协方差和去奇异值:
def pca(X):
"""
pca函数
:param X:
:return:
"""
# 计算协方差
sigma = (X.T @ X) / len(X)
# 计算奇异值
U, S, V = np.linalg.svd(sigma)
return U, S, V
X_norm, means, stds = featureNormalize(X)
U, S, V = pca(X_norm)
画出计算后的向量:
plt.figure(figsize=(7, 5))
plt.scatter(X[:, 0], X[:, 1], facecolors='none', edgecolors='b')
plt.plot([means[0], means[0] + 1.5 * S[0] * U[0, 0]],
[means[1], means[1] + 1.5 * S[0] * U[0, 1]],
c='r', linewidth=3, label='First Principal Component')
plt.plot([means[0], means[0] + 1.5 * S[1] * U[1, 0]],
[means[1], means[1] + 1.5 * S[1] * U[1, 1]],
c='g', linewidth=3, label='Second Principal Component')
plt.grid()
# changes limits of x or y axis so that equal increments of x and y have the same length
# 改变x或y轴的极限,使x和y的增量相等,长度相同
# 不然看着不垂直,不舒服。:)
plt.axis("equal")
plt.legend()
plt.show()
如图是在两个维度上的向量:

数据映射,将点映射到一维向量上:
def projectData(X, U, K):
"""
映射数据
:param X:
:param U:
:param K:
:return:
"""
Z = X @ U[:, :K]
return Z
数据恢复,将映射到向量上的点恢复到二维:
def recoverData(Z, U, K):
"""
恢复数据
:param Z:
:param U:
:param K:
:return:
"""
X_rec = Z @ U[:, :K].T
return X_rec
调用一下,首先将二维的点映射到一维向量上,得到1.49这个相对坐标,然后用1.49与该向量进行恢复,恢复到1.05左右:
Z = projectData(X_norm, U, 1) # [1.49631261] print(Z[0]) X_rec = recoverData(Z, U, 1) # [-1.05805279 -1.05805279] print(X_rec[0])
画图:
plt.figure(figsize=(7, 5))
plt.axis("equal")
plot = plt.scatter(X_norm[:, 0], X_norm[:, 1], s=30, facecolors='none',
edgecolors='b', label='Original Data Points')
plot = plt.scatter(X_rec[:, 0], X_rec[:, 1], s=30, facecolors='none',
edgecolors='r', label='PCA Reduced Data Points')
plt.title("Example Dataset: Reduced Dimension Points Shown", fontsize=14)
plt.xlabel('x1 [Feature Normalized]', fontsize=14)
plt.ylabel('x2 [Feature Normalized]', fontsize=14)
plt.grid(True)
# 画虚线
for x in range(X_norm.shape[0]):
plt.plot([X_norm[x, 0], X_rec[x, 0]], [X_norm[x, 1], X_rec[x, 1]], 'k--')
# 输入第一项全是X坐标,第二项都是Y坐标
plt.legend()
plt.show()
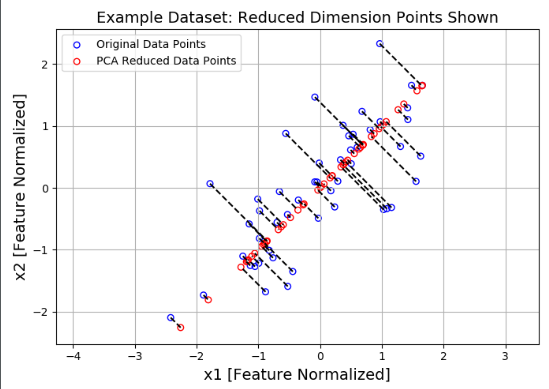
4.在人脸图像上使用PCA
压缩前:

PCA选择后的36种颜色:

数据恢复后,可以看出确实恢复了一部分数据:

代码:
# -*- coding:utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
from scipy.io import loadmat
def featureNormalize(X):
means = X.mean(axis=0)
stds = X.std(axis=0, ddof=1)
X_norm = (X - means) / stds
return X_norm, means, stds
def pca(X):
sigma = (X.T @ X) / len(X)
U, S, V = np.linalg.svd(sigma)
return U, S, V
def projectData(X, U, K):
Z = X @ U[:, :K]
return Z
def recoverData(Z, U, K):
X_rec = Z @ U[:, :K].T
return X_rec
mat = loadmat('data/ex7faces.mat')
X = mat['X']
# (5000, 1024)
print(X.shape)
def displayData(X, row, col):
fig, axs = plt.subplots(row, col, figsize=(8, 8))
for r in range(row):
for c in range(col):
axs[r][c].imshow(X[r * col + c].reshape(32, 32).T, cmap='Greys_r')
axs[r][c].set_xticks([])
axs[r][c].set_yticks([])
plt.show()
displayData(X, 10, 10)
X_norm, means, stds = featureNormalize(X)
U, S, V = pca(X_norm)
# (1024, 1024) (1024,)
print(U.shape, S.shape)
displayData(U[:, :36].T, 6, 6)
z = projectData(X_norm, U, K=36)
X_rec = recoverData(z, U, K=36)
displayData(X_rec, 10, 10)
0 条评论