【深度学习笔记】激活函数集合

本篇写一些对激活函数的一些理解。如果有错误欢迎各位大佬指出。

首先是损失函数的一般要求：

• 非线性。非线性保证了网络的深度；使用线性激活函数会让多层网络坍塌成一层。
• （几乎）处处可微。可微性保证了在优化中的梯度可计算性。
• 计算简单。这也就是为什么Relu比exp类激活函数要更受欢迎。
• 非饱和性。饱和指的是在某些区间梯度接近0，从而导致梯度消失。最典型的例子是sigmoid。

sigmoid

图像如下：

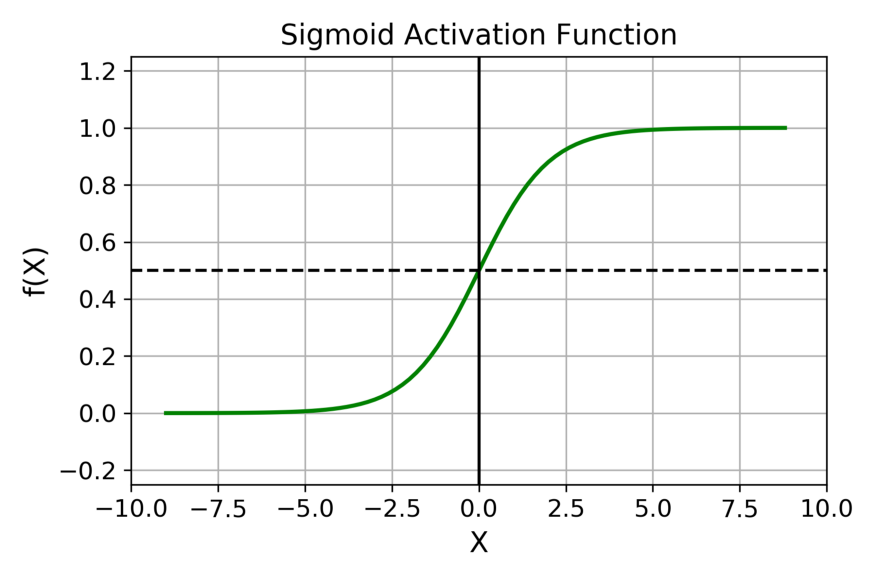
公式如下：

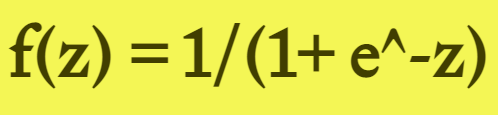
sigmoid非常适合将概率作为输出的模型，因为概率的取值范围是0～1。

优点：

• 梯度平滑，避免「跳跃」的输出值；
• 明确的预测，即非常接近 1 或 0。

缺点：

• 倾向于梯度消失（由于两侧的饱和区域）
• 指数运算的计算代价较大
• 输出不以0为中心，降低了权重更新的效率。

tanh

图像为：

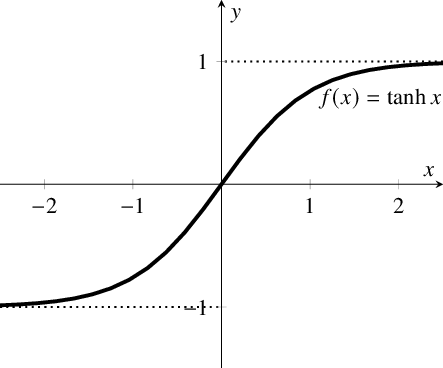
公式为：

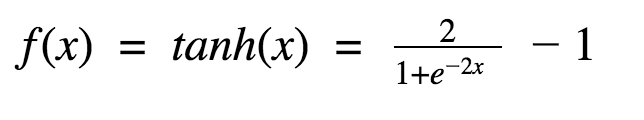
tanh 是一个双曲正切函数。tanh 函数和 sigmoid 函数的曲线相对相似。但是它比 sigmoid 函数更有一些优势。

优点：

• 梯度平滑，避免「跳跃」的输出值；
• 输出以0为中心。

缺点：

• 倾向于梯度消失（由于两侧的饱和区域）
• 指数运算的计算代价较大

ReLU

图像为：

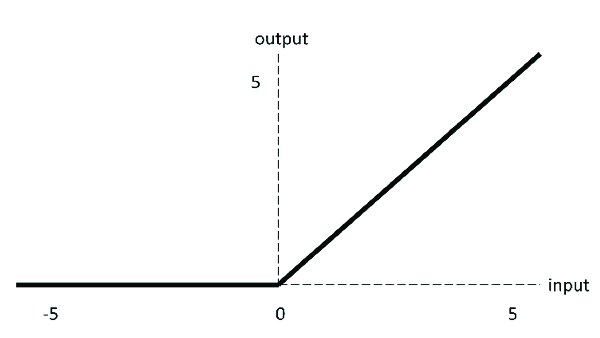
公式为：

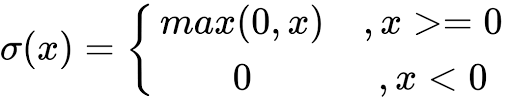
ReLU目前在深度学习中比较流行，相比sigmoid和tanh有很多优点，但是也有缺点。（PS：关于ReLU更多的思考详见ReLU的思考）

优点：

• 计算简单，没有复杂的指数运算
• 当输入为正时，不存在梯度饱和

缺点：

• ReLU不是以0为中心的
• Dead ReLU问题。反向传播过程中可能会产生0梯度（正向中的0可以理解，毕竟有些地方敏感有些地方不敏感，但是反向传播如果输入负数则会产生0梯度）

Leaky ReLU

为了解决Dead ReLU问题，提出了Leaky ReLU

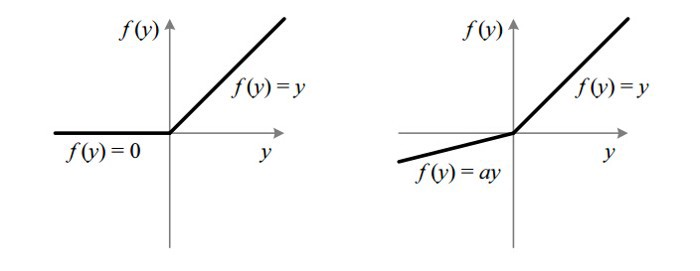
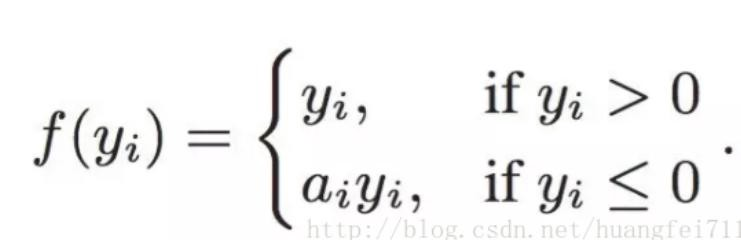
Leaky ReLU通过给负区间一个很小的斜率（0.01）来解决Dead ReLU问题。

理论上讲，Leaky ReLU拥有ReLU所有的优点，同时又不会有ReLU的问题。但是尚未证明Leaky ReLU总比ReLU好。

GeLU

公式为：

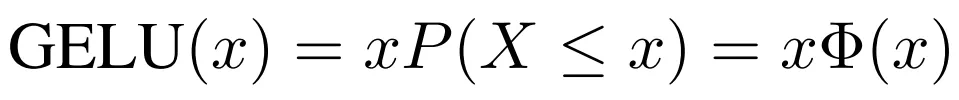
这个是无法计算的，通过数学公式逼近为：

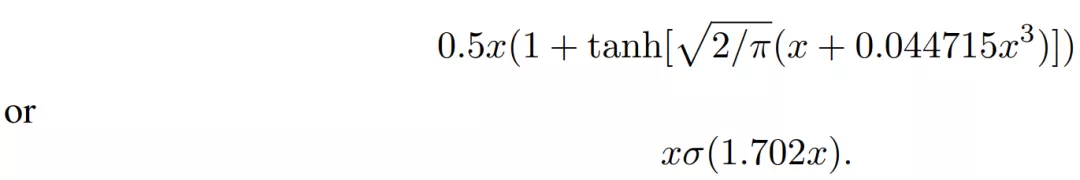
也可以说是x*sigmoid(x)

图像为：

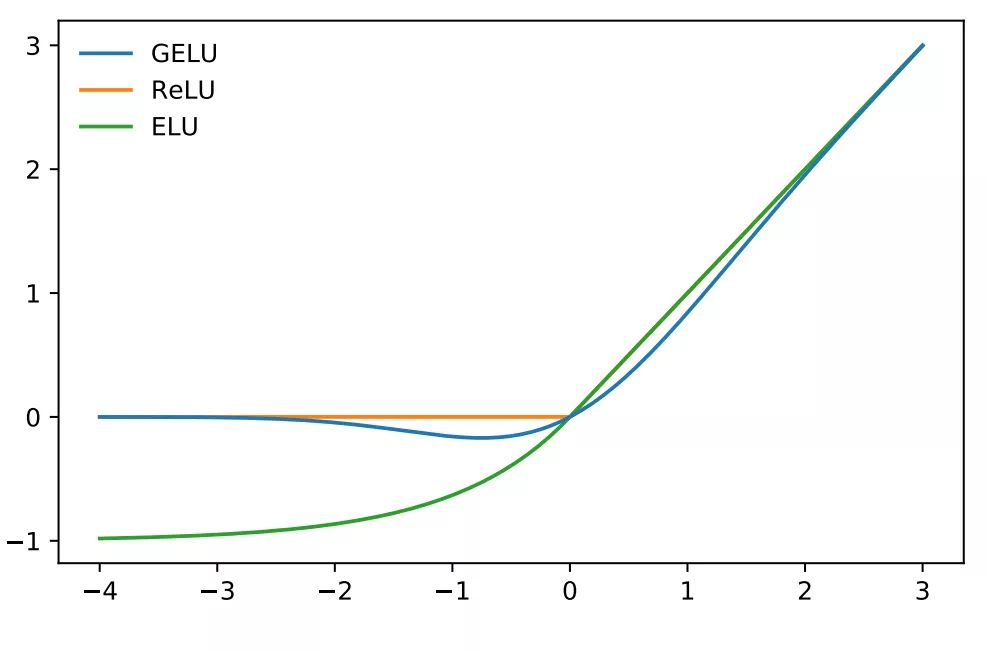
目前Berts，GPT-2等模型中均使用了GELU激活函数。

---

最后，谷歌大脑还尝试了很多简单函数组合来作为激活函数（arXiv:1710.05941），有兴趣的同学可以去读一读。