在上一篇文章中,我们了解了注意力——这是一种在现代深度学习模型中普遍存在的一种方法。注意力机制是一个有助于提高机器翻译性能的概念。在这篇文章中,我们将着眼于Transformer——一个使用注意力来提高这些模型的训练速度的模型。在特定的任务中,Transformer的性能能够优于谷歌的机器翻译模型。这是很大的提升,然而,这些提升是来自于Transformer能够进行并行运算。事实上,谷歌云建议使用Transformer来作为参考模型来使用它们的TPU云。因此,让我们拆开这个模型看看他到底是怎么工作的。
Transformer是由论文Attention is all you need提出。基于Tensorflow的实现可以用Tensor2Tensor包。哈佛大学的NLP小组创建了一个使用pytorch的实现版本。这篇文章中,我们尝试将事情简化一点,并逐一介绍各个部分,希望大家有一个深刻的理解。
概览
让我们首先把模型当做一个黑盒。在机器翻译应用中,他将获取一种语言的句子,然后输出另一种语言。

打开Transformer,我们可以发现编码部分和解码部分,以及他们中间的一个连接。
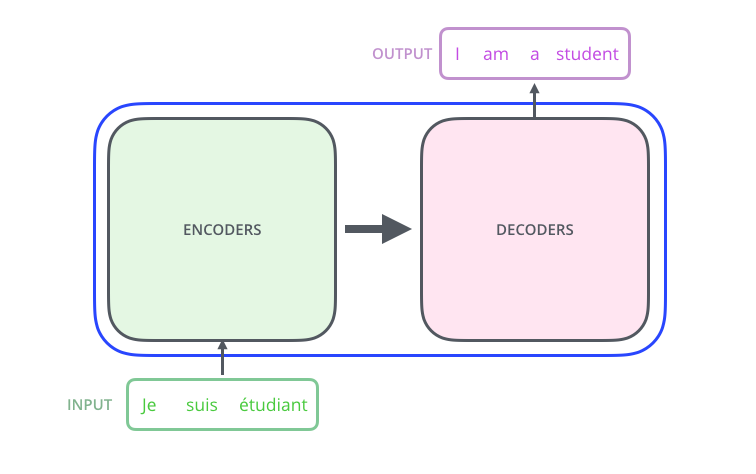
编码部分是由一堆编码器组成的(论文中由6个编码器组成,6并不是什么神奇的数字,你可以尝试别的数字)。解码器大小相同。
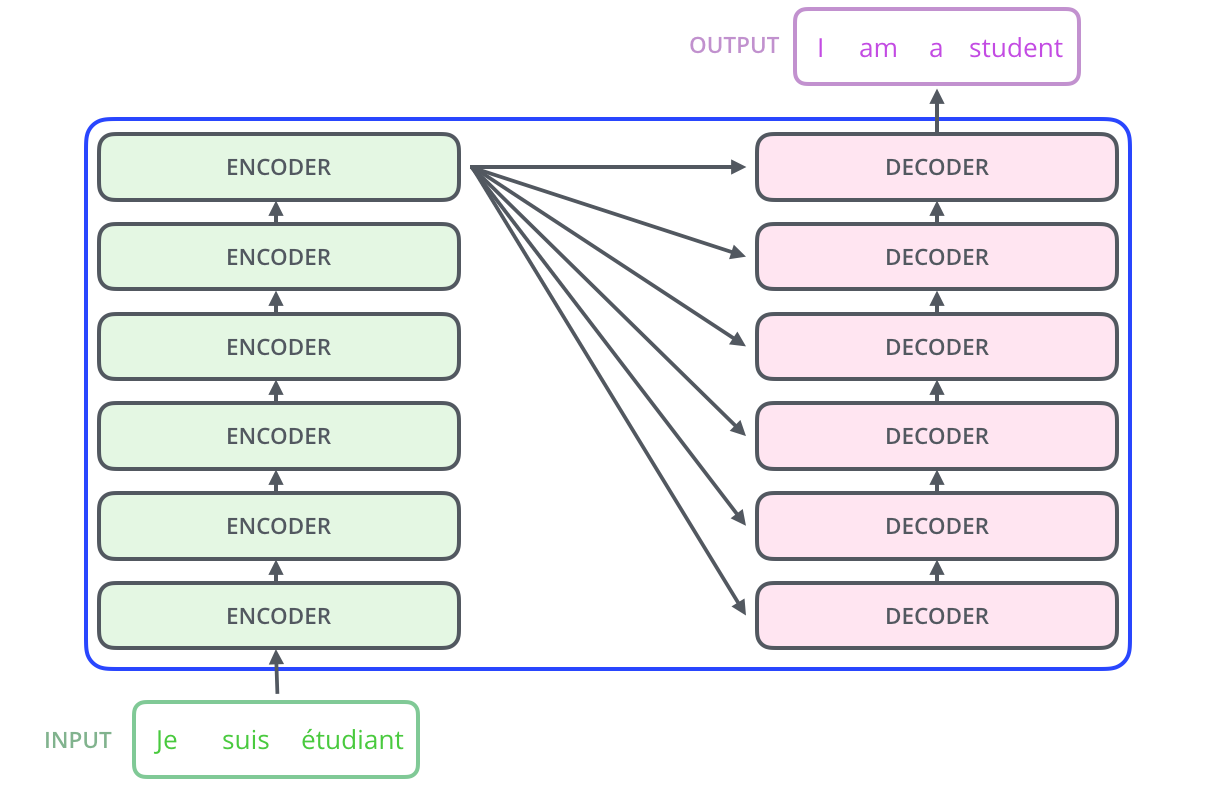
所有的编码器在结构上都是相同的(但是并不共享权重),每一层都有两个子层。
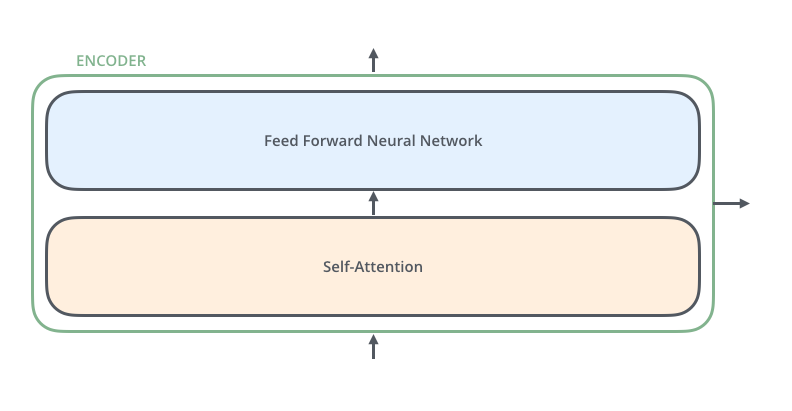
输入数据首先通过一个自注意力层——这层能够帮助编码器在对特定单词编码器时查看输入句子中的其他单词。我们将稍后在文章中介绍自注意力。
自注意力层的输出被送入一个前馈神经网络中。在每一个地方完全相同且独立的使用这个前馈神经网络。
解码器也有这两层,但是在注意力层和前向传播层中多了一个注意力层。这层可以帮助解码器关注输入句子中的每一个相关部分(和seq2seq的注意力很像。)
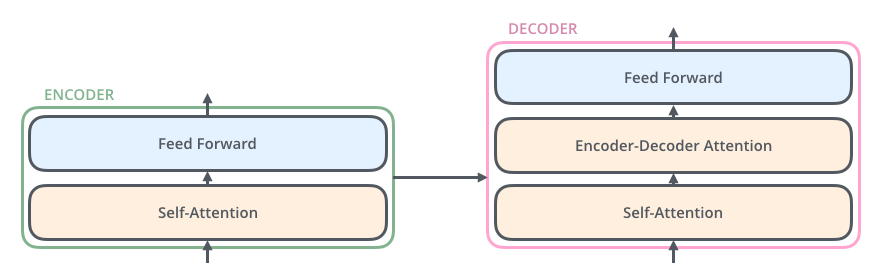
我们把张量代入带图中
现在,我们已经看到了模型的主要组成部分,让我们看看各种向量(张量)以及他们是如何在各个组件之间流动的,从而将输入转换为输出。
与NLP的一般流程一样,我们首先使用词嵌入将每个输入字转换成一个向量。

词嵌入只发生在编码器的最底层。所有编码器都输入一个大小为512的向量(最底层为词向量,而其它层是前一层的输出)。这个尺寸的大小是一个我们可以调整的超参——基本上这是我们训练集中最长的句子长度。
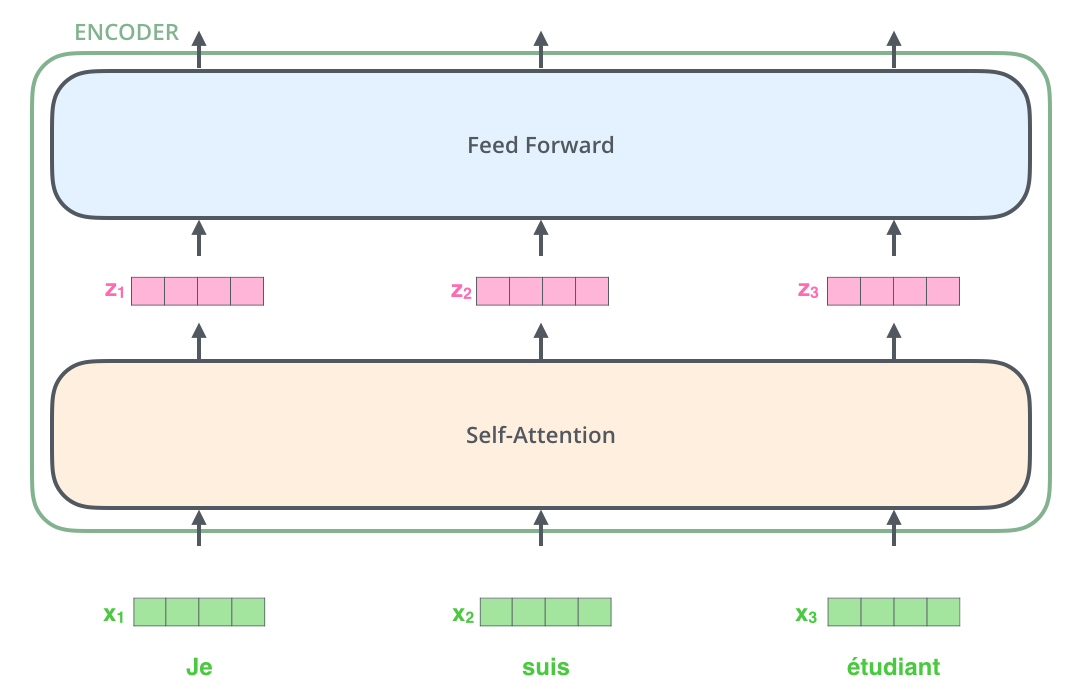
在这里,我们看到Transformer关键的地方,即每个向量在解码器上的流动的路径。在自注意力层中,这些路径之间存在依赖关系(注:就是它们要互相“查看”来完成注意力)。然而,前馈层没有这些依赖项,因此各种路径可以在流经前馈层时并行。
接下来,我们将把这个例子转换成一个更短的句子,我们看一看在编码器的每个子层中发生了什么。
现在我们进行编码
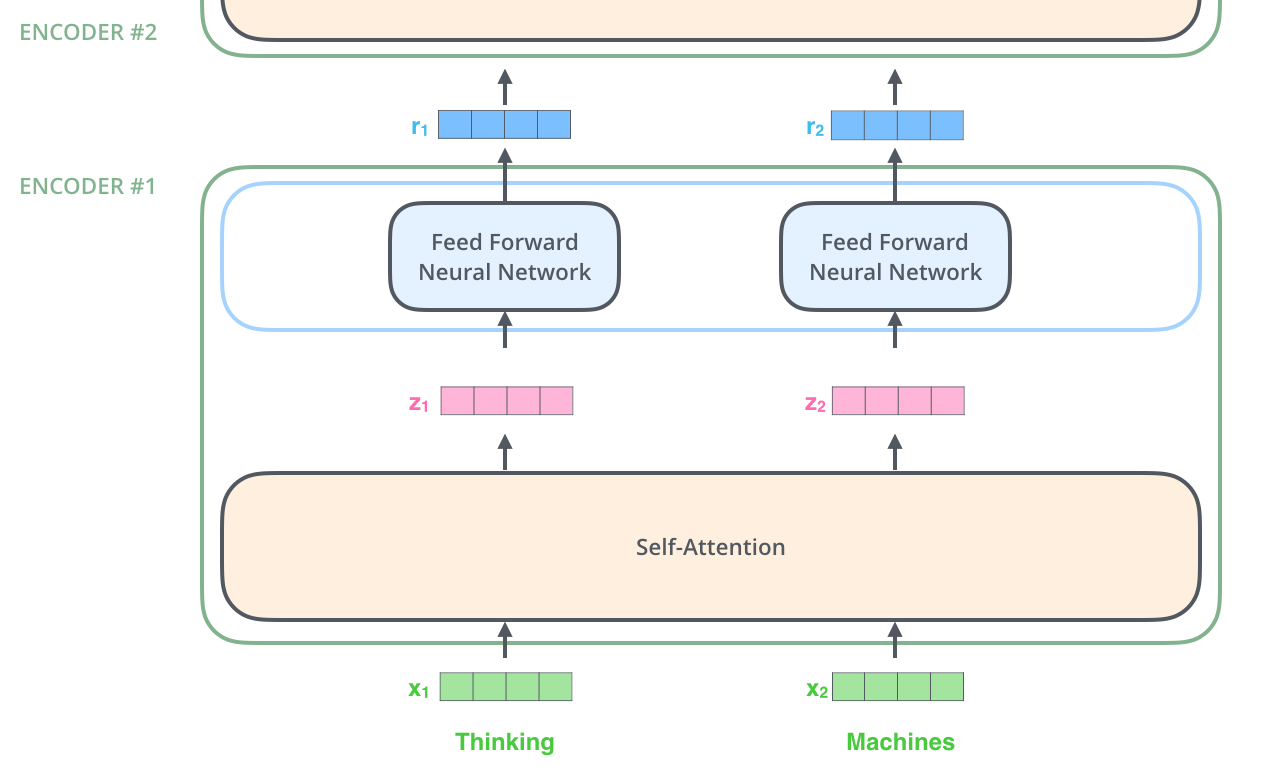
正如我们已经提到的,编码器接受一系列的向量作为输入。他通过将这些向量传递到一个自注意力层来处理这个列表,然后传递到一个前馈神经网络中,然后输出作为下一个编码器的输入。
高层次的自注意力
不要被我说的“自注意力”这个词迷惑了,就好像这是一个每个人都应该知道的概念。我本人在读Attention is all you need这篇论文之前从没听说过注意力。让我们看看他到底是怎么工作的。
假设下面的句子是我们要翻译的句子:
”The animal didn't cross the street because it was too tired”
这个句子的it指的是什么?是指街道还是动物?这对于人类来说是一个简单的问题,但是对于算法来说却并不简单。
当模型在处理it时,自注意力让it和animal联系起来。
当模型处理每个单词(输入序列中的每个位置)时,自注意力能够关注输入句子中的其他位置,这能够产生对这个单词进行更好的编码。
如果你对RNNs很熟悉,思考怎样维护一个隐藏状态来允许RNN将它处理过的先前单词( 向量 )与它正在处理的单词(向量)结合起来。自注意力Transformer使用的方法,使能更好的理解当前处理的词。

自注意力的细节
让我们先看一看如何使用张量来计算自注意力,然后再来看一看如何实现——使用矩阵。
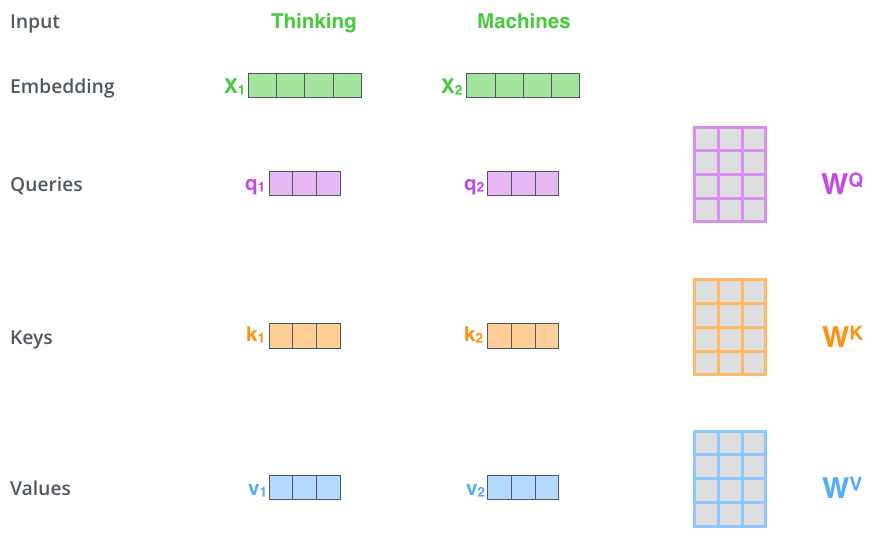
自注意力的第一步是从每个编码器的输入创建三个向量(在本例中是每个单词的嵌入)。因此对于每个单词,我们创建一个查询向量(Query,Q)、关键字向量(Key,K)、和一个值向量(Value,V)。这些向量是通过将嵌入和我们在训练阶段获得的三个矩阵相乘得到的。
主义,这些新的向量比嵌入向量的维度要要小。他们的维度是64,而输入的嵌入向量为512维。他们并不是必须变小,这只是一种(大部分)多头注意力的一种结构。
什么是‘query’、‘key’、‘value’向量?
他们是注意力进行计算和思考的一个抽象概念。一旦你开始阅读下面关于如何计算注意力的部分,你将知道这些向量是如何工作的。
自注意力的第二步是计算一个分数。假设我们正在计算这个例子中第一个单词‘thinking’的自注意力,我们需要给输入句子中的没一个单词打分。当我们在某个位置对单词进行编码时,分数决定了我们对输入语句的其它部分的关注程度。
分数是通过query向量和key向量点积计算出来的。因此如果我们在第一层进行自注意力,第一个分数将是q1和k1的点乘。第二个分数将是q1和k2的点乘。
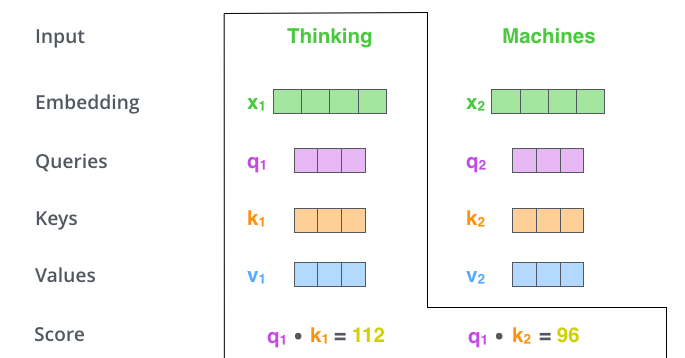
第三步和第四步是将分数除以8(论文默认是8,因为是向量维度64的开根号,这会使得梯度更加稳定),然后将结果进行softmax操作。softmax操作将各个点的分数和变成1(就是变成概率)。
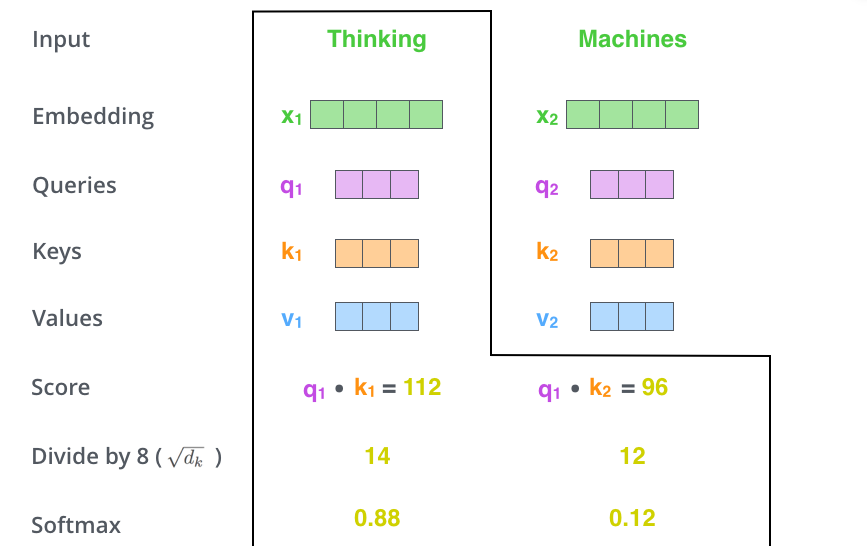
这个softmax分数决定了每个单词在这个位置的表达量(权重)。很明显,这个位置的单词的分数会最高,但是这在观察当前单词和其他单词关系时可能很有用。
第五步是将每个value向量乘以softmax得分(然后求和)。这里的直觉是保持我们想要关注的单词值,而不在关注那些我们不想要的词(通过成语像0.001这类的数字)
第六步是对加权后的value向量求和。这将会在这个位置产生自注意力层的输出(对于第一个单词)
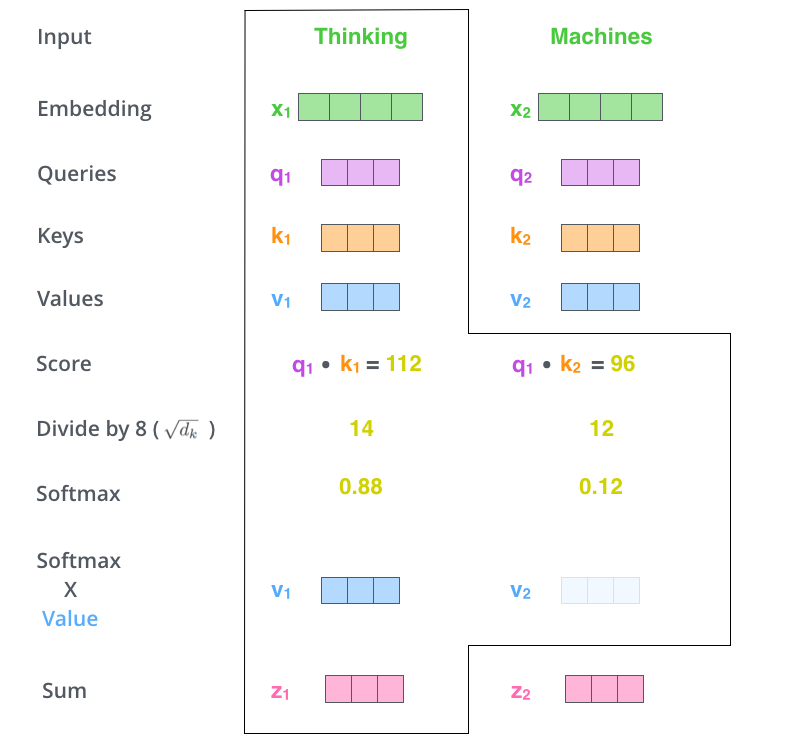
这就是自注意力的结果。我们可以将输出向量送到前馈神经网络。然而,在实际运行中,这种计算是以矩阵形式进行的,这样会更快的进行计算。现在我们再来看看矩阵形式的计算。
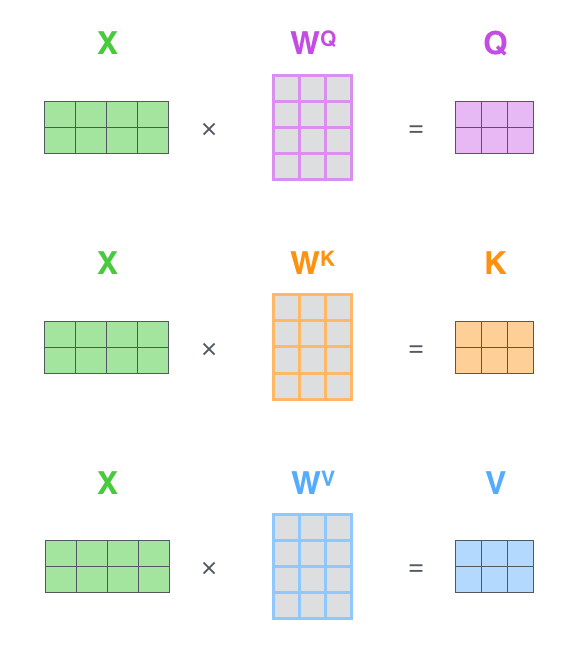
X矩阵中的每一行对应于输入句子的一个单词。(实际上嵌入向量512维,图上4维,输出向量(q、k、v)64维,图上3维)
最后,由于我们处理的是矩阵,我们可以将2~6步压缩成一个公式来计算输出。
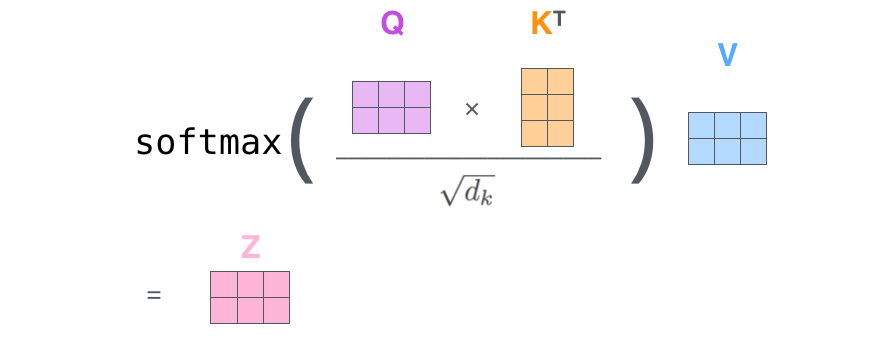
多头的野兽
本文进一步细化了自注意力层,增加了一个多头注意力机制。这在两个方面提高了注意力机制的表现:
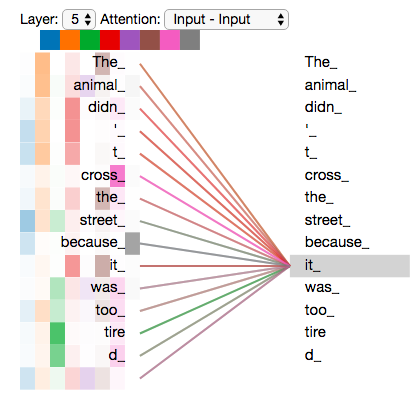
1.它扩展了模型关注不同位置的能力。就像上面举的例子,z1包含了一些其他地方的编码。但是它仍然可以由单词本身决定。比如我们翻译一个句子“ The animal didn’t cross the street because it was too tired ”我们将会知道it指代的是什么。
2.它为注意力层提供了“表示子空间(representaion subspaces)”。就像下面我们即将看到的,使用多头注意力机制会有多个Query、Key、Value权重矩阵。(Transformer使用了8头注意力机制)。每一个矩阵都是随机初始化的。然后,在训练之后,每一个集合(Q、K、V)将被用来进行输入嵌入到不同的表示子空间中。
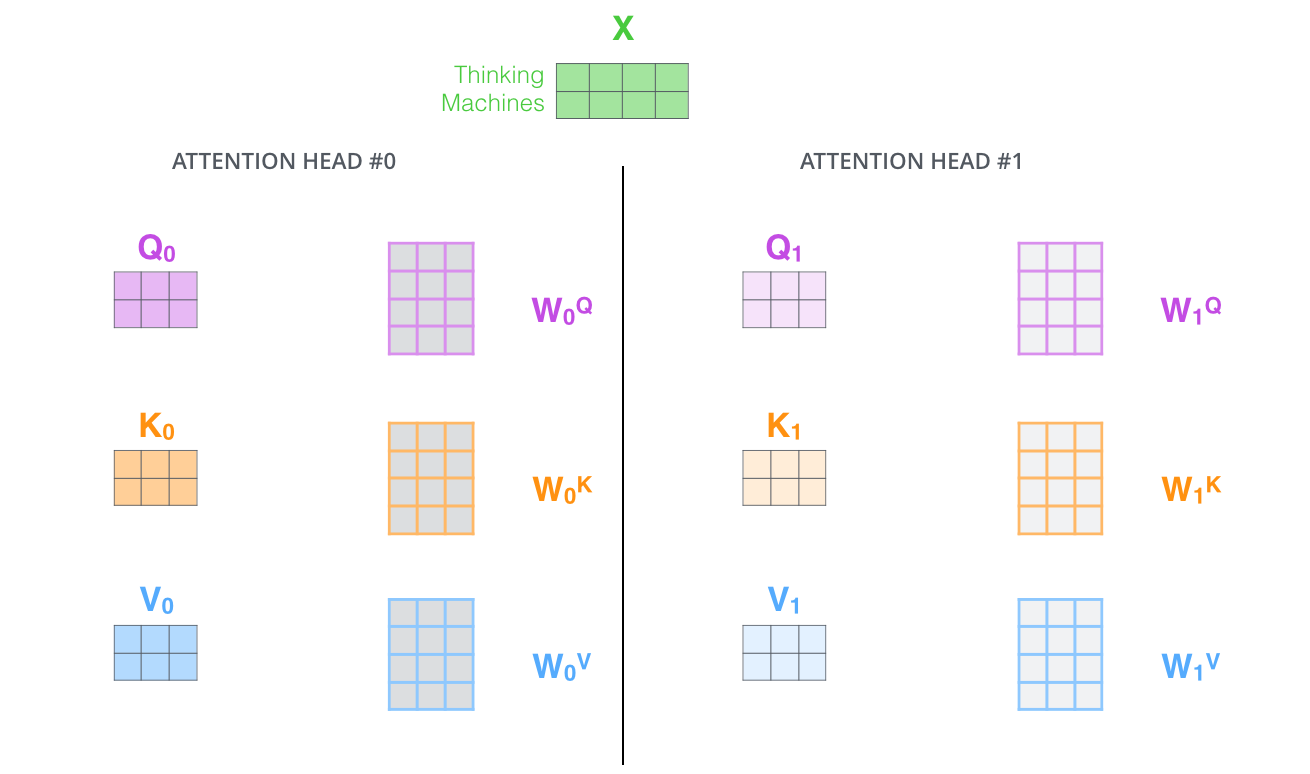
如果我们做同样的自注意力计算,只是使用不同的权重矩阵做8次,那么我们最终会得到8个不同的权重矩阵Z。
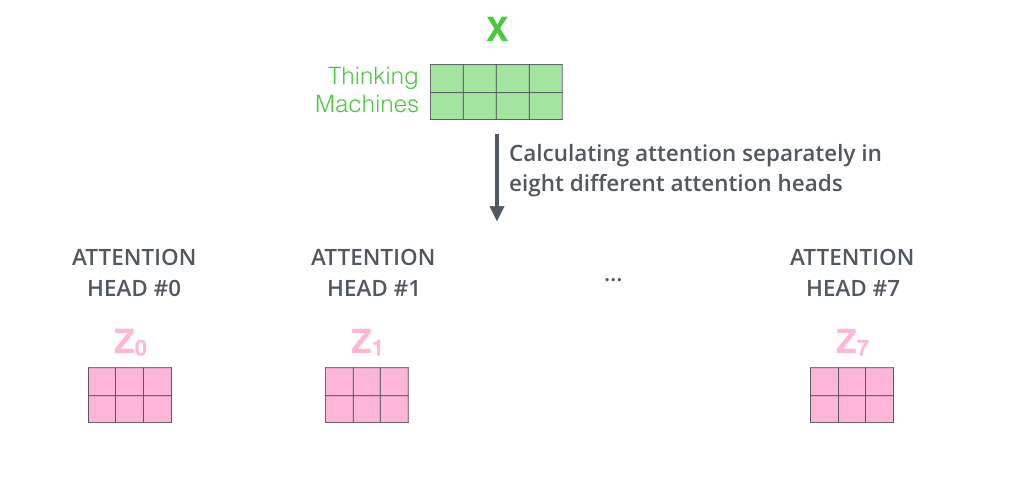
这给我们带来了一些挑战。前向传播层并不需要8个矩阵——它只需要一个矩阵(每个单词对应一个向量)。所以我们需要一种方法把这8个矩阵压缩成一个矩阵。
我们怎么做呢?我们将8个矩阵放到一起,然后使用另一个矩阵做矩阵乘法。
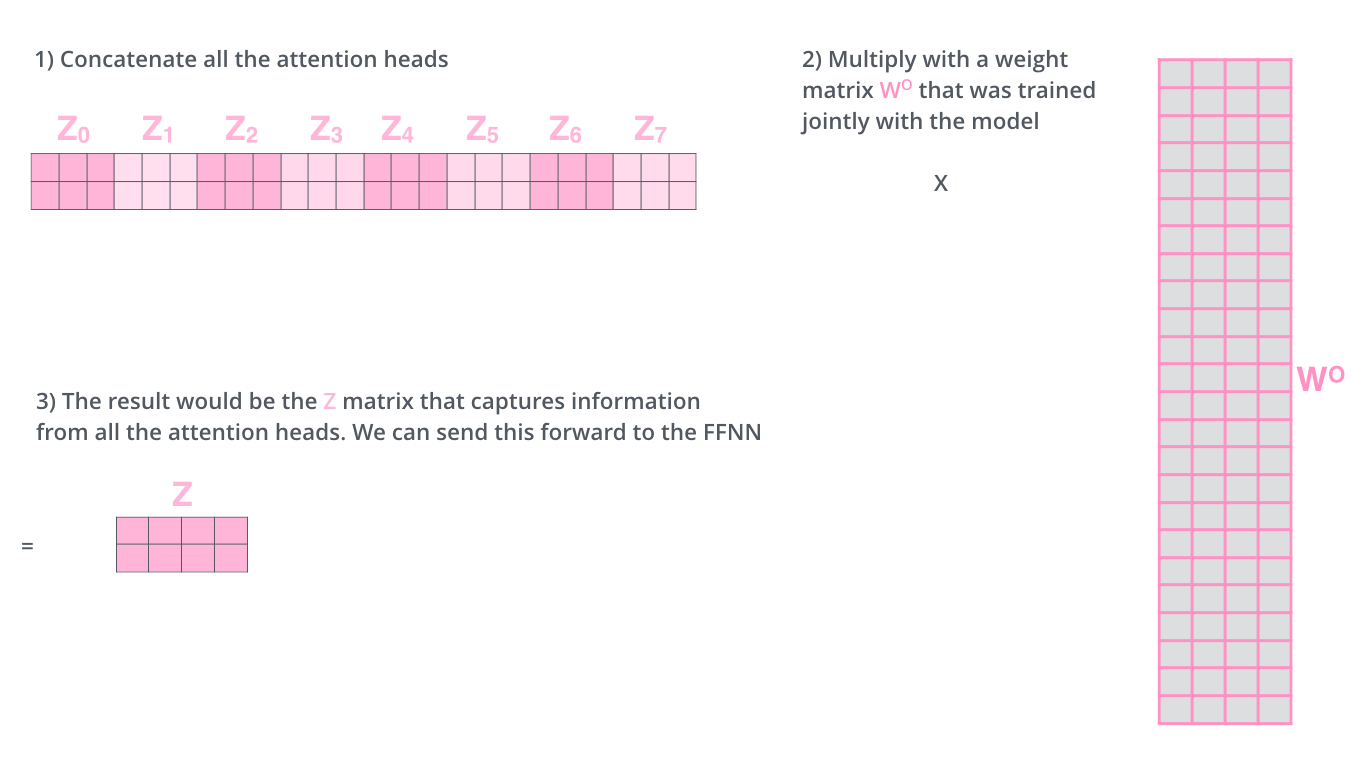
这就是多头注意力机制。确实有很多矩阵。让我们试着把他们都放在一个可视化环境中。
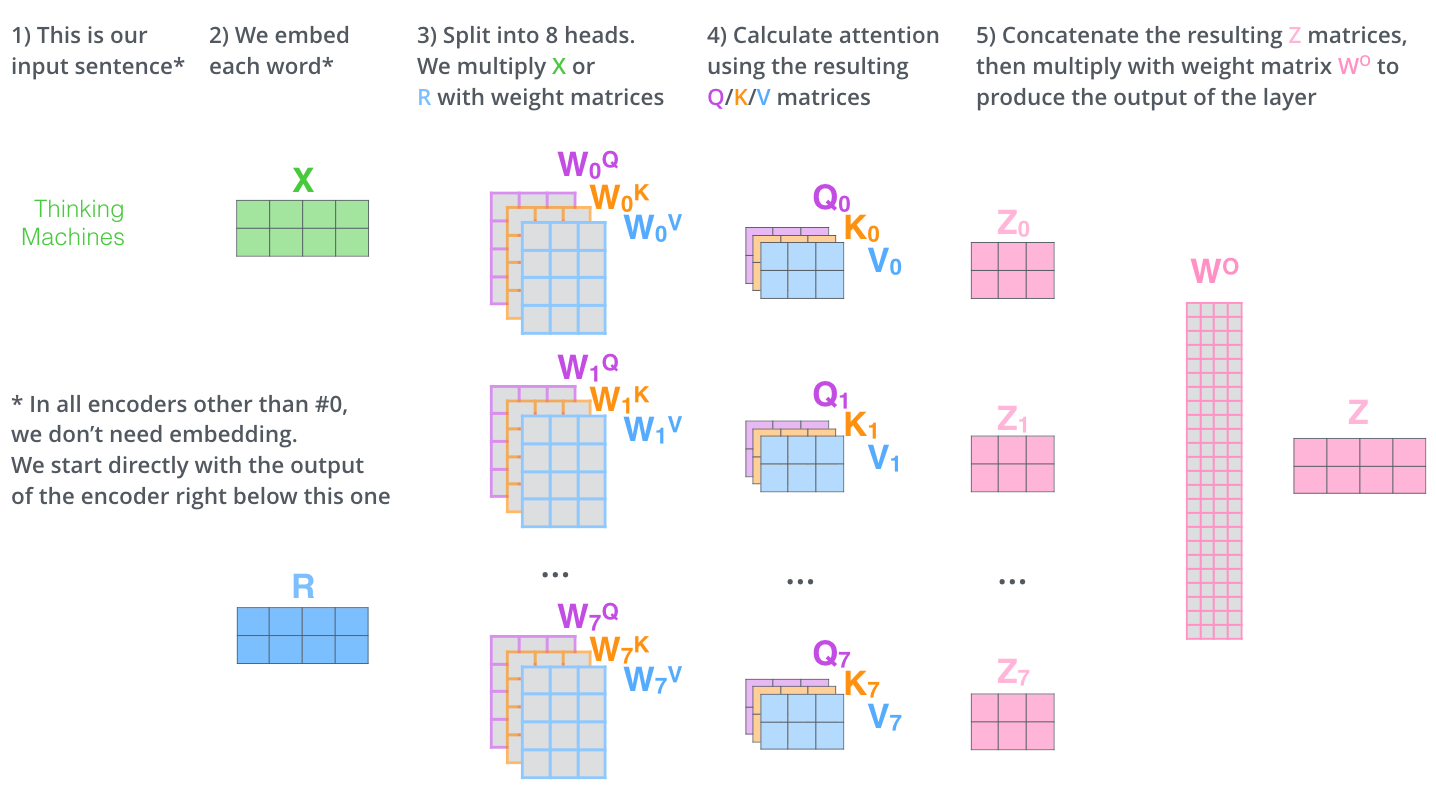
现在我们已经接触到了注意力头,让我们重新思考前面的例子,当我们对it进行编码时,不同的注意力头在关注什么?

如果我们将所有的8个头都放在一起表示:
使用位置编码来表示序列的顺序
到目前为止,我们所描述的模型中缺少的一件事是解释输入序列中单词顺序的方法。
为了解决这个问题,Transformer向每个词嵌入中添加一个向量。这些向量可以被学习出来,并且这个向量有助于确定每个单词的位置或者不同单词在句子中的间隔。
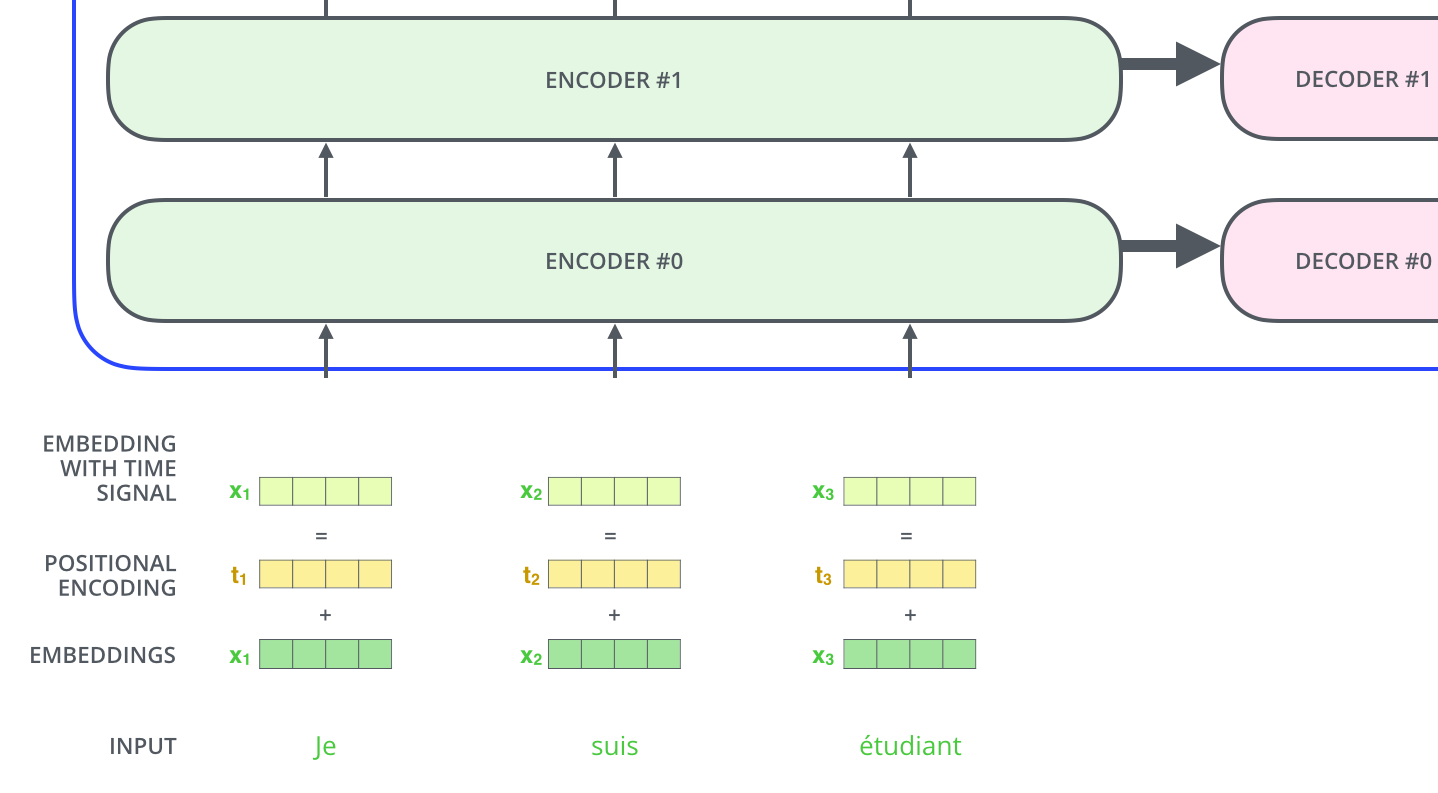
我们假设嵌入的维度是4,那么是实际上的编码过程是这样的。
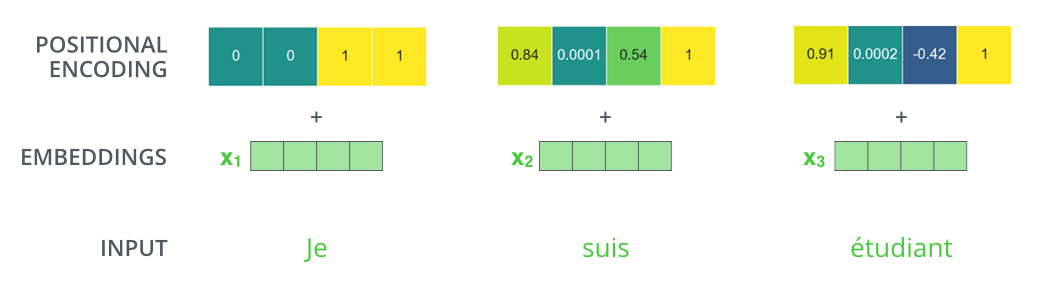
这个模型可能是什么样的?
在下面的图中,每一行对应一个向量的位置编码,所以第一行就是我们在输入序列中嵌入第一个单词时添加的向量。每一行包括512个值,每个值介于1和-1之间。我们用不同的颜色来表示他们,这样我们就可以可视化了。
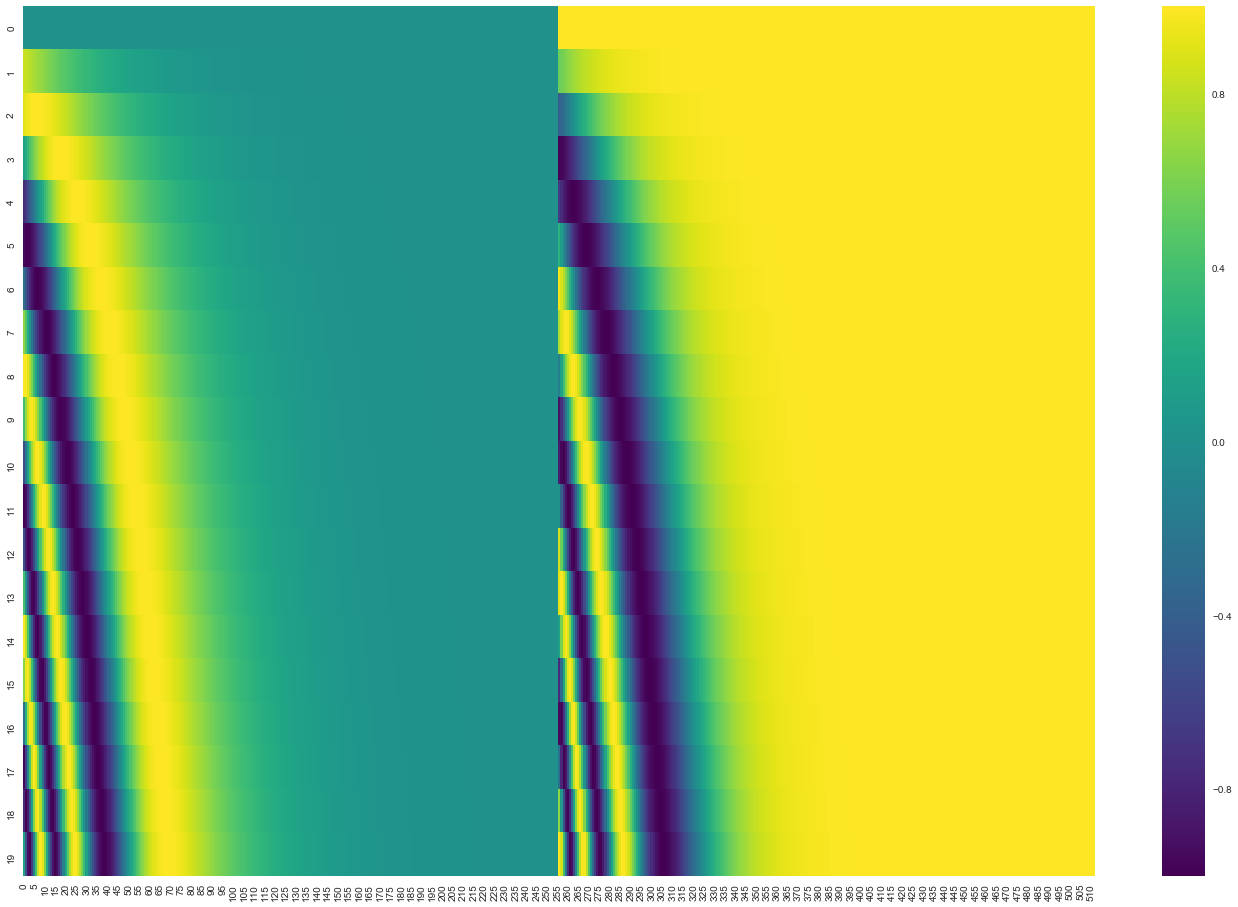
一个生成位置编码的方法:
def get_timing_signal_1d(length,
channels,
min_timescale=1.0,
max_timescale=1.0e4,
start_index=0):
"""Gets a bunch of sinusoids of different frequencies.
Each channel of the input Tensor is incremented by a sinusoid of a different
frequency and phase.
This allows attention to learn to use absolute and relative positions.
Timing signals should be added to some precursors of both the query and the
memory inputs to attention.
The use of relative position is possible because sin(x+y) and cos(x+y) can be
expressed in terms of y, sin(x) and cos(x).
In particular, we use a geometric sequence of timescales starting with
min_timescale and ending with max_timescale. The number of different
timescales is equal to channels / 2. For each timescale, we
generate the two sinusoidal signals sin(timestep/timescale) and
cos(timestep/timescale). All of these sinusoids are concatenated in
the channels dimension.
Args:
length: scalar, length of timing signal sequence.
channels: scalar, size of timing embeddings to create. The number of
different timescales is equal to channels / 2.
min_timescale: a float
max_timescale: a float
start_index: index of first position
Returns:
a Tensor of timing signals [1, length, channels]
"""
position = tf.to_float(tf.range(length) + start_index)
num_timescales = channels // 2
log_timescale_increment = (
math.log(float(max_timescale) / float(min_timescale)) /
(tf.to_float(num_timescales) - 1))
inv_timescales = min_timescale * tf.exp(
tf.to_float(tf.range(num_timescales)) * -log_timescale_increment)
scaled_time = tf.expand_dims(position, 1) * tf.expand_dims(inv_timescales, 0)
signal = tf.concat([tf.sin(scaled_time), tf.cos(scaled_time)], axis=1)
signal = tf.pad(signal, [[0, 0], [0, tf.mod(channels, 2)]])
signal = tf.reshape(signal, [1, length, channels])
return signal
当然这并不是位置嵌入的唯一方式。
残差
在继续向下讲之前,我们需要知道一个细节,就是在每一个编码器中间的子层都有一个残差(residual)连接,跟在标准化之后。
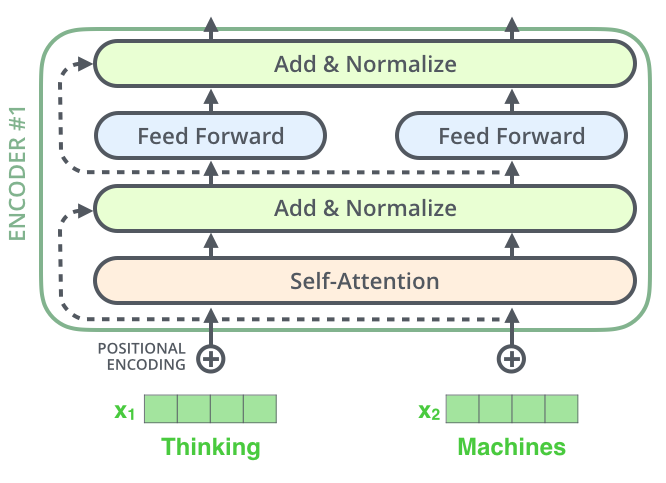
如果我们将向量和标准化层和自注意力层进行可视化,如下:
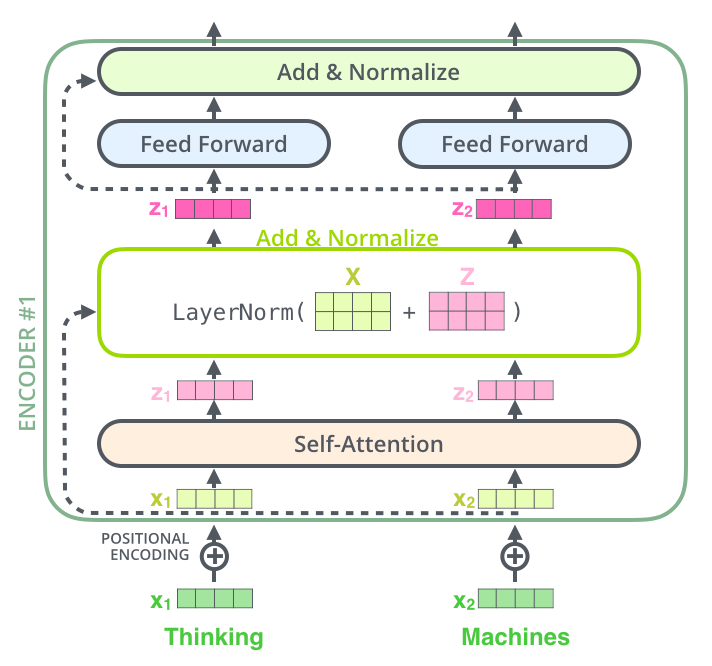
这也适用于解码器的子层。如果我们考虑一个由2层堆叠的编码器和解码器,如下图:
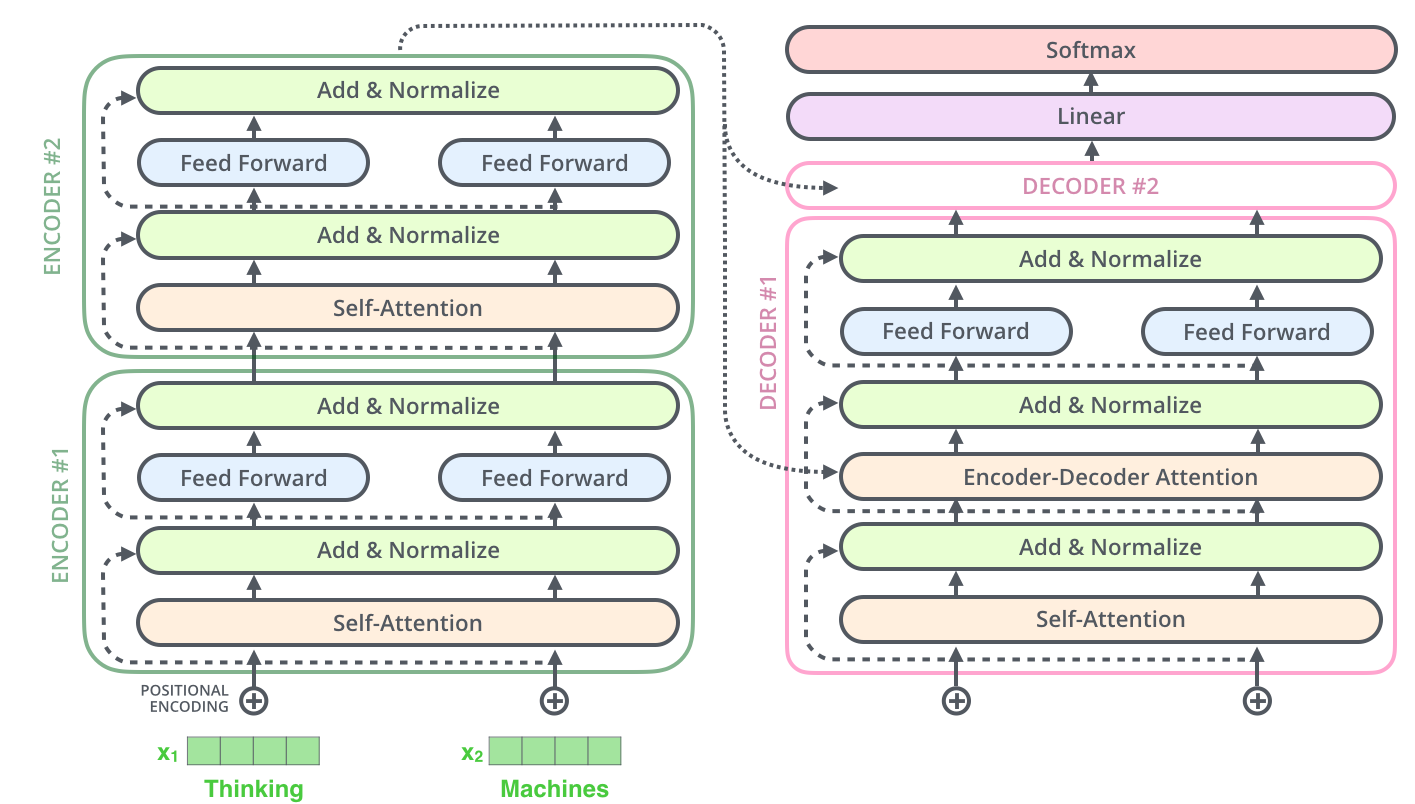
解码器端
现在我们已经知道了 编码器部分的大部分工作,我们基本上也知道了解码器是如何工作的。
编码器首先处理输入序列,然后将顶层编码器的输出转换乘一组注意力向量K和V。然后被解码器在‘encoder-decoder Attention’层中使用,这有助于将注意力集中在输入序列的适当位置。
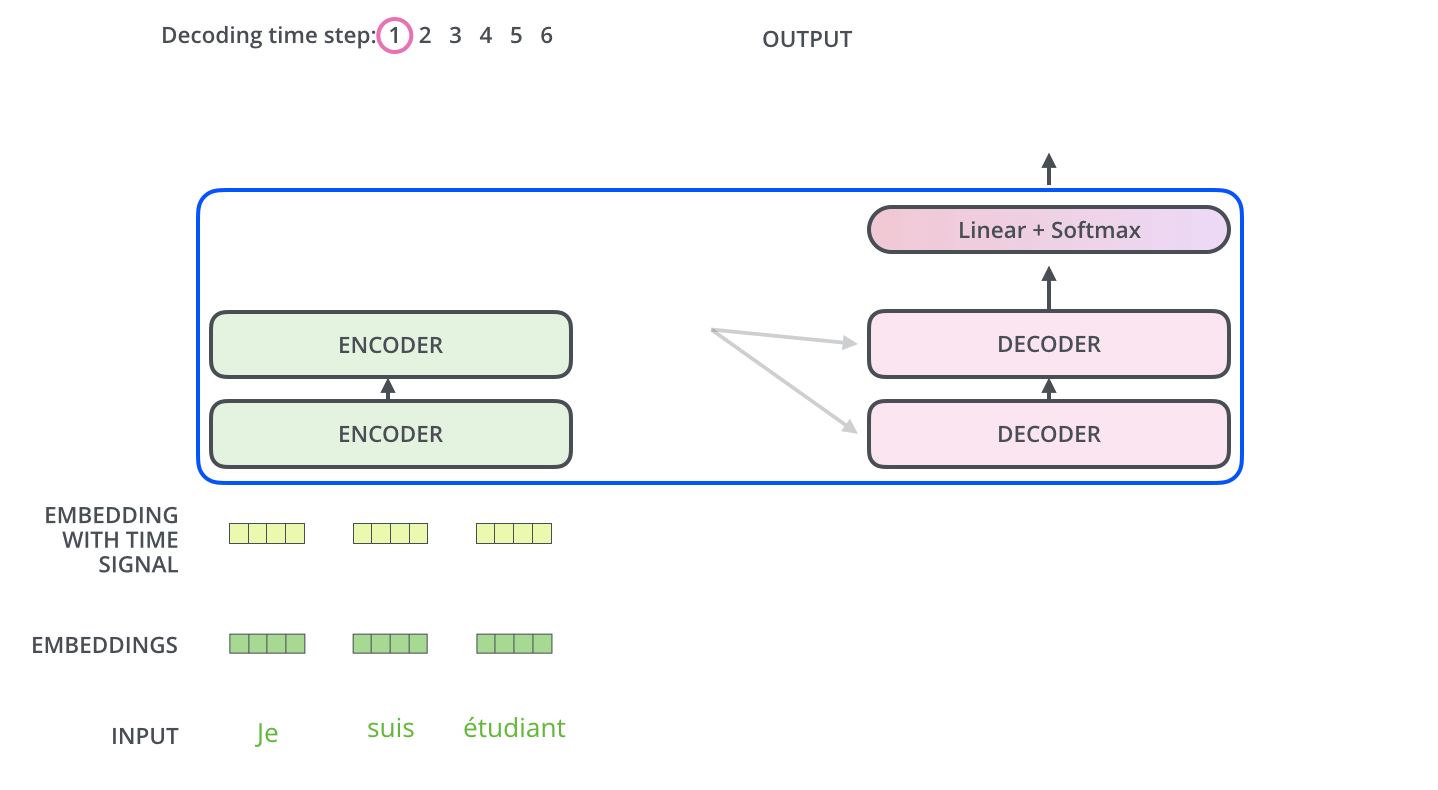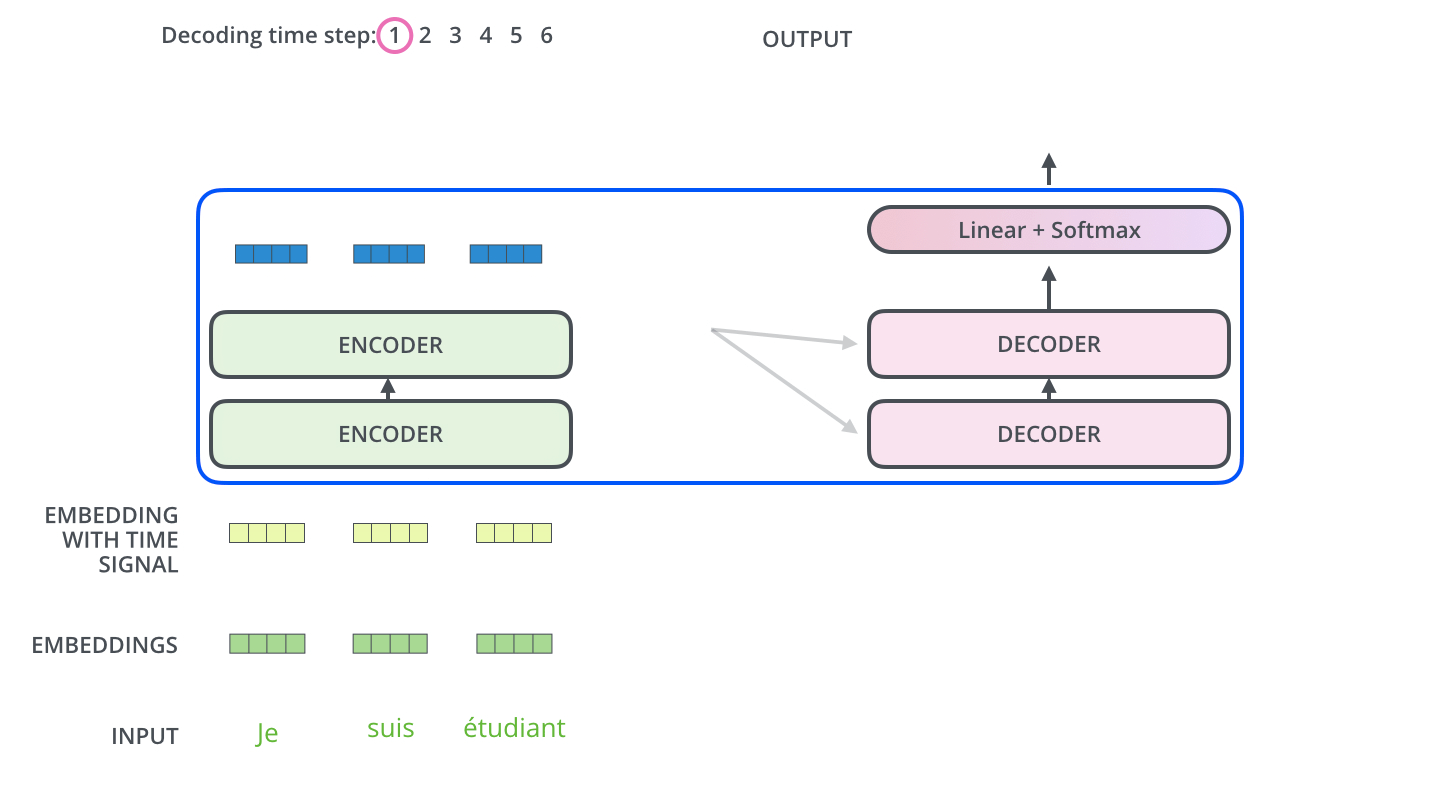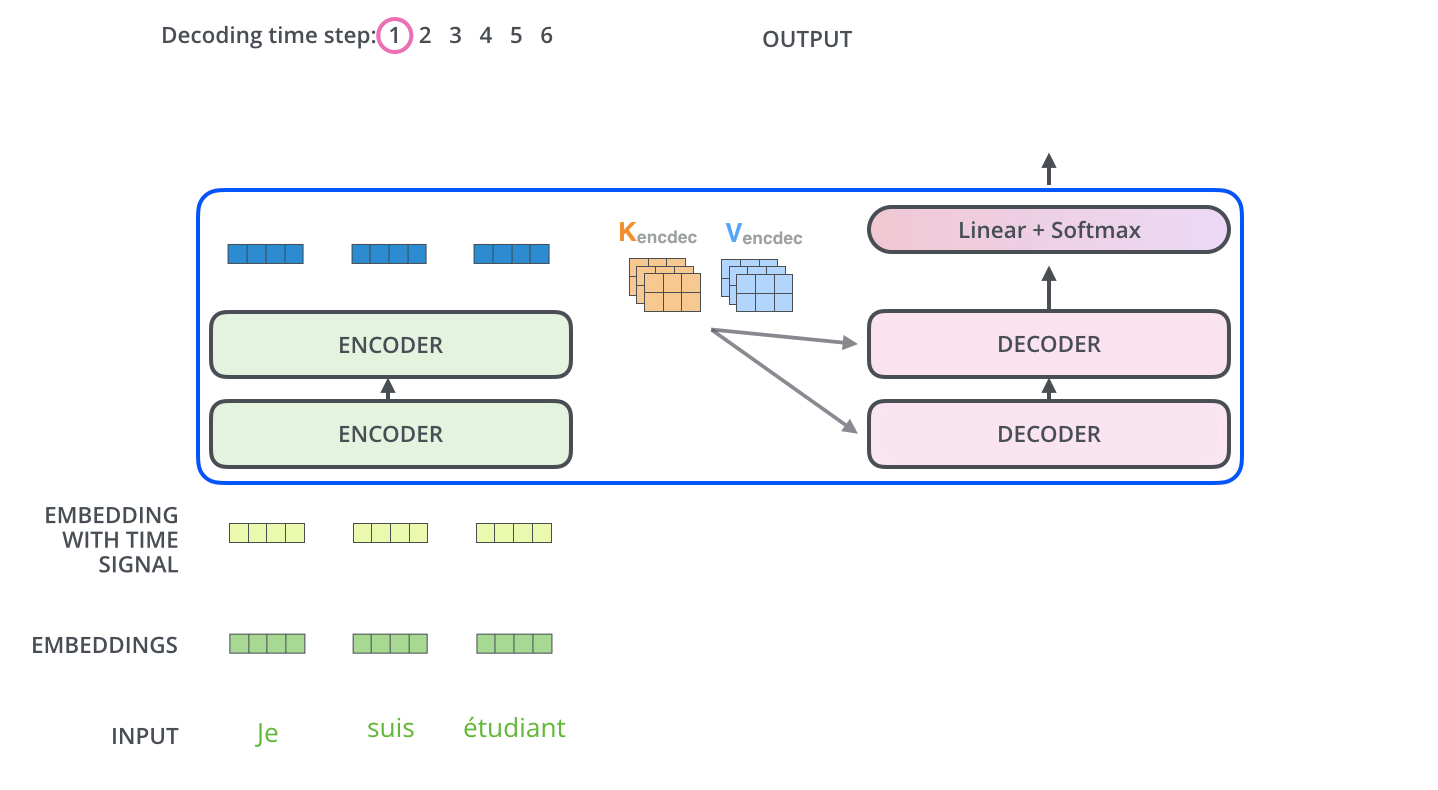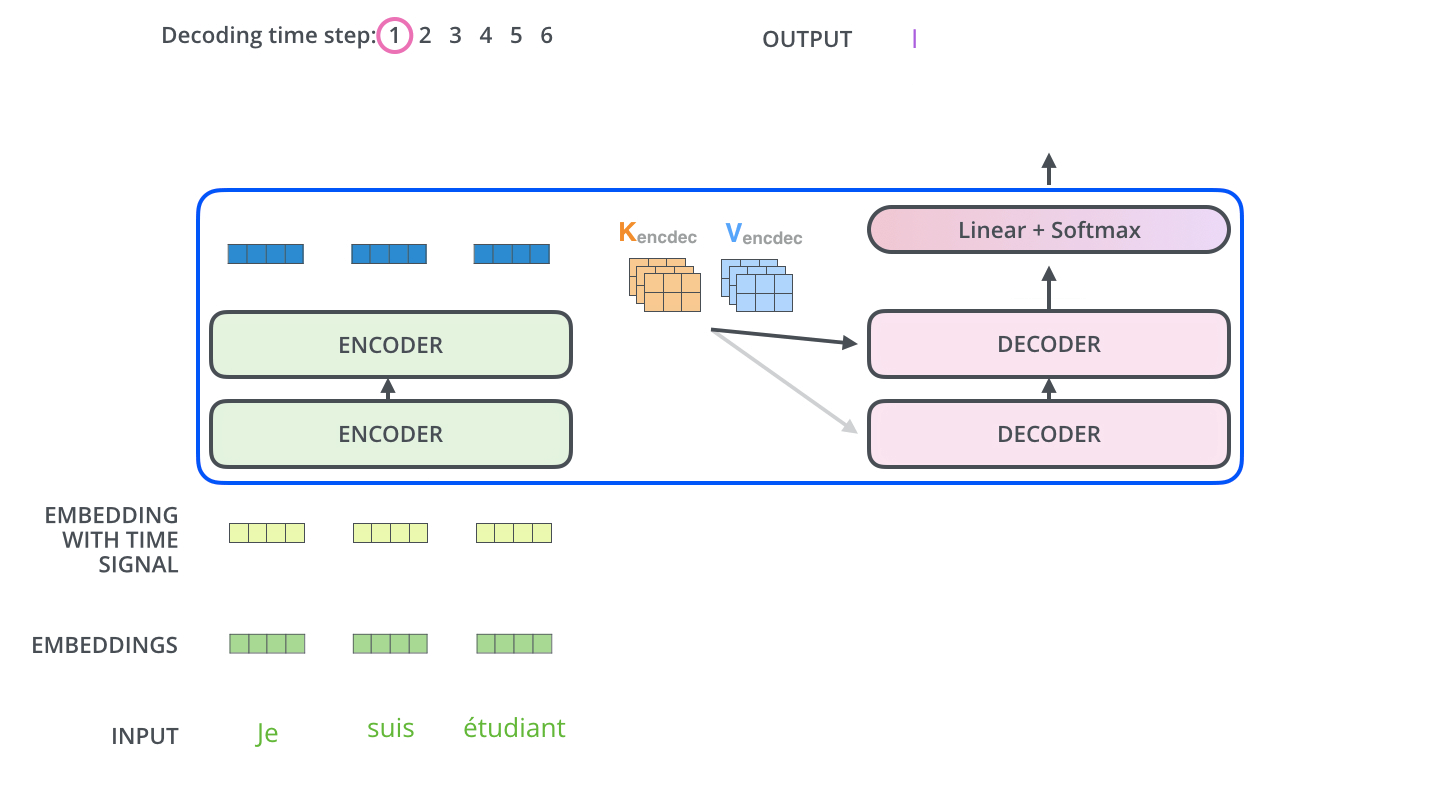
然后重复这个过程,直至达到一个特殊符号,完成输出。输出的每一步都被用来作为下一步的输入,然后解码器就像编码器做的一样(指词嵌入)。就像我们对编码器输入所做的一样,我们将词嵌入和位置嵌入加到一起来表示每一个单词。
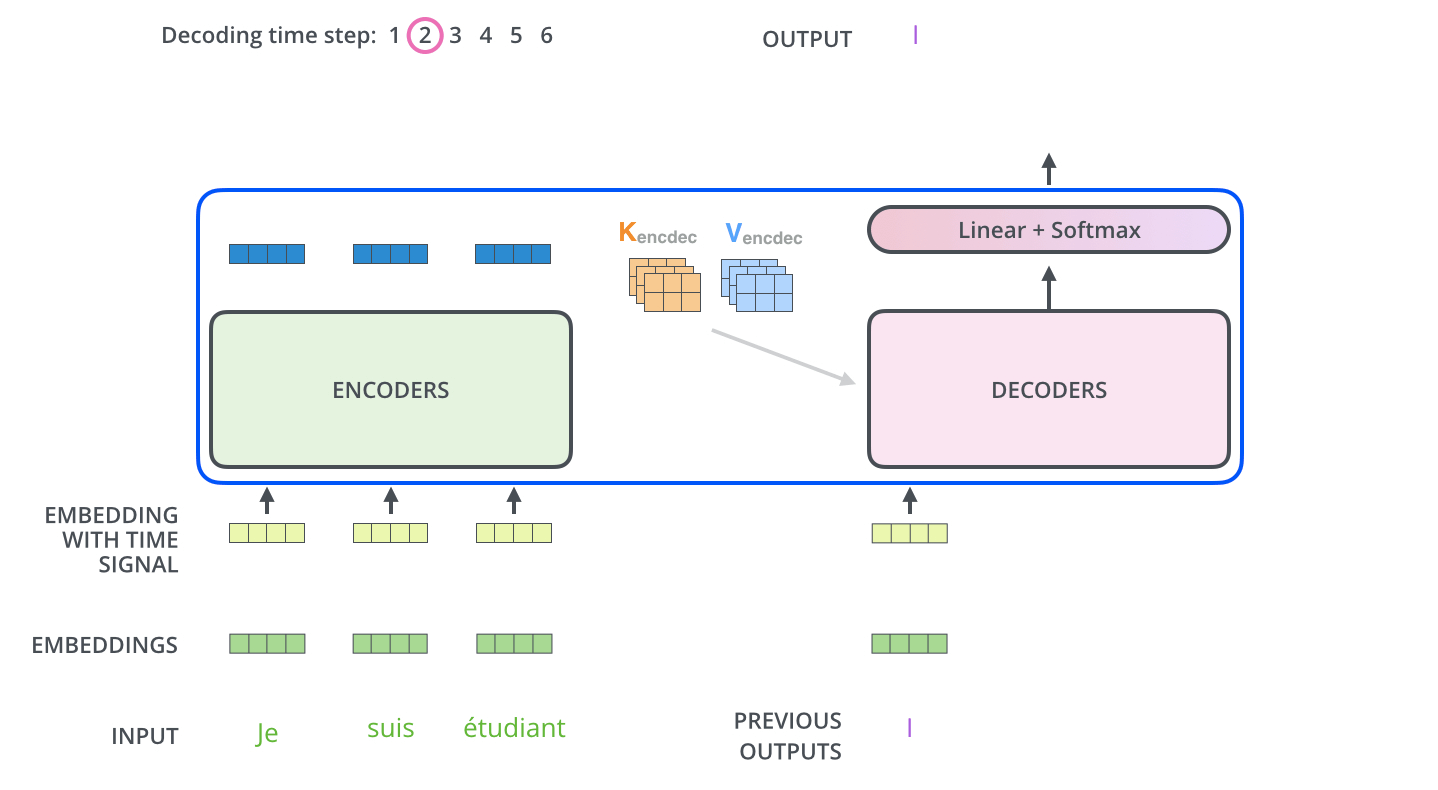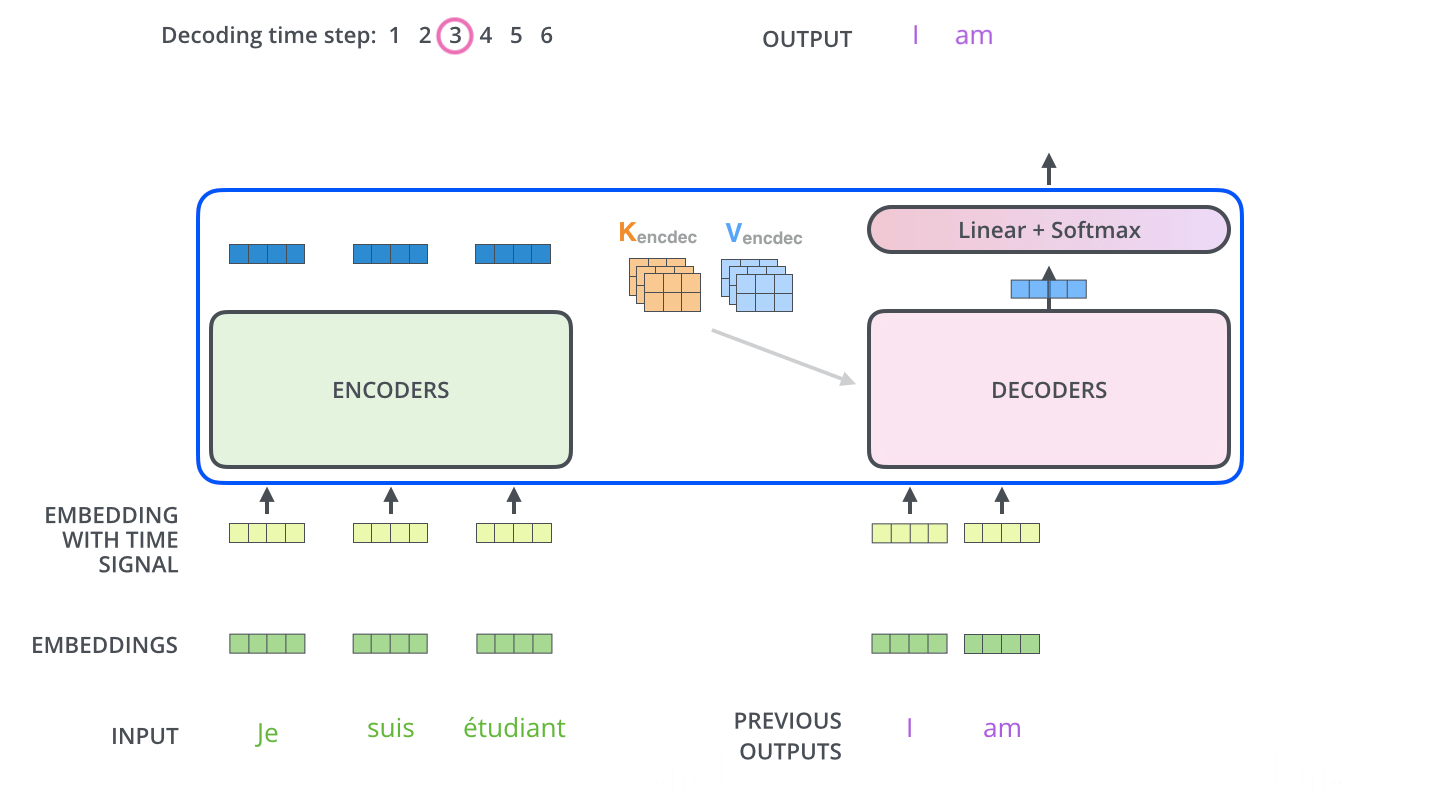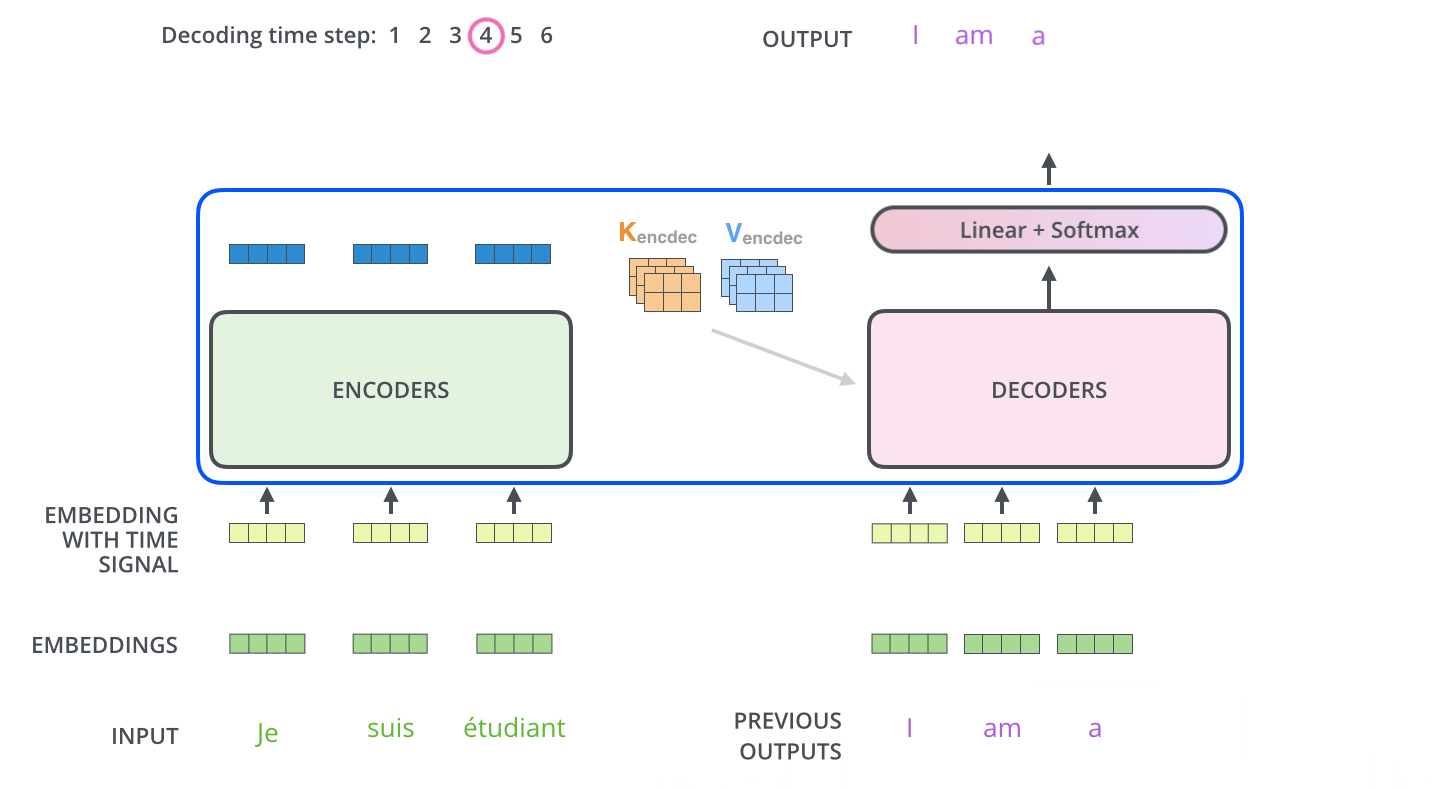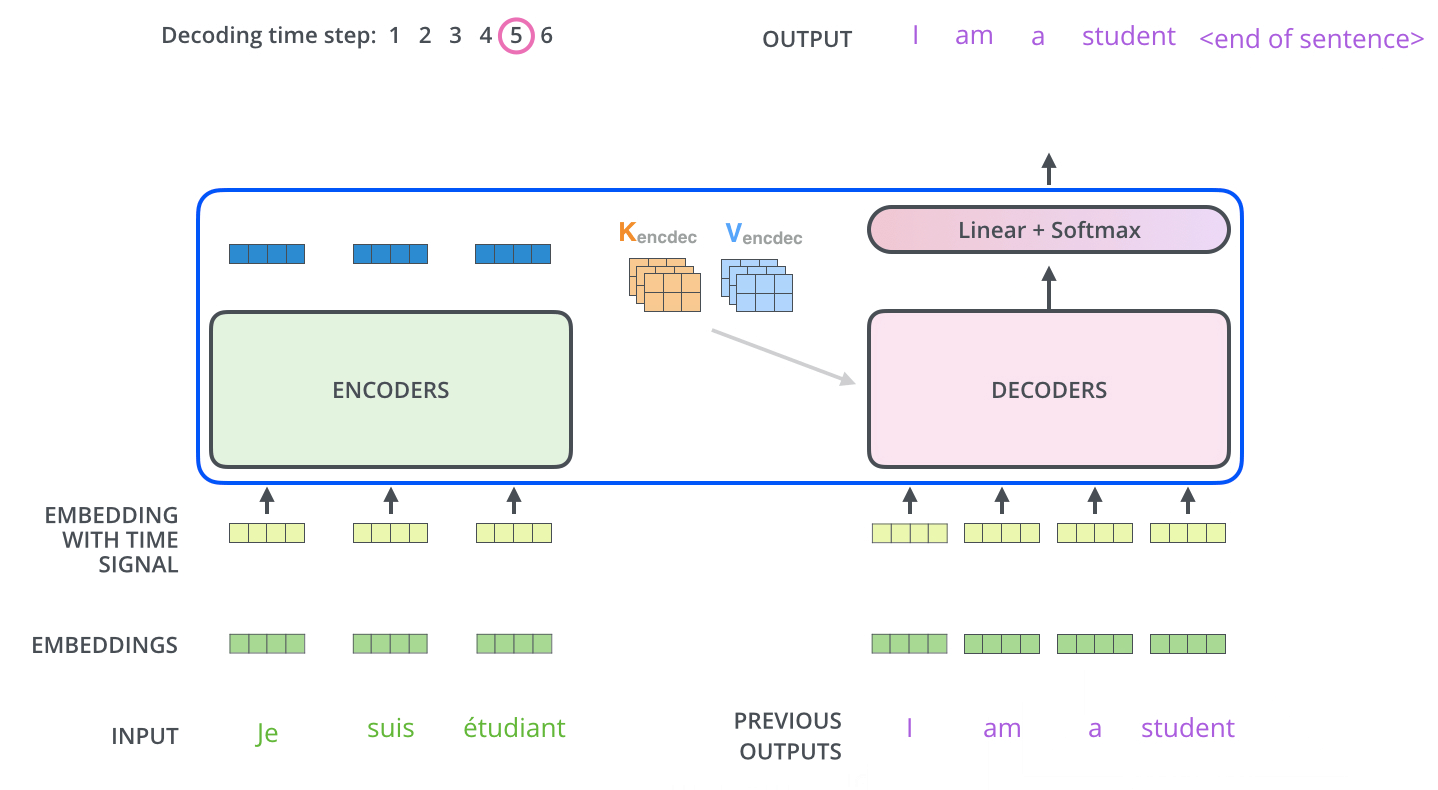
解码器中的自注意力层稍微有点不同:
在解码器中,自注意力层只允许注意输出序列中较早的位置(左侧)。这是通过在softmax前将后面的位置都设置为-inf来完成的。
‘encoder-decoder Attention’层原理类似于多头注意力机制,只是它从下一层获取Q矩阵,并从从编码层的输出中获取K和V矩阵。
最后的线性和Softmax层
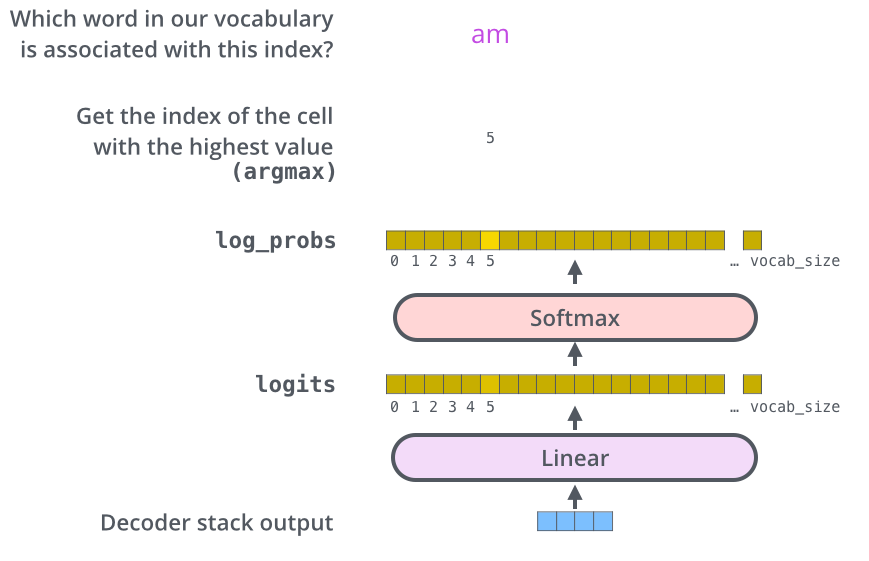
解码器最后输出一个浮点型向量,那么我们怎么将它转换成单词呢?这就需要线性层和Softmax层。
线性层就是一个简单的全连接神经网络,它将解码器产生的向量投影到一个更大的逻辑向量上。
我们假设我们的训练集有10000个单词,这将使逻辑向量的长度为10000,每一个单元格对应一个单词的得分。
然后softmax层将这些得分转换为一个概率(均为正,和为1)。选取概率最大的单元格,并生成与之关联的单词作为这一时间步的输出。
训练
现在我们已经知道了一个训练好的Transformer是如何工作的,那么Transformer是怎么训练的呢?
我们在训练过程中,我们可以通过当前网络输出和实际的正确输出做对比。
我们假设输出词汇表中只有6个单词: (“a”, “am”, “i”, “thanks”, “student”, and “<eos>” ( ‘end of sentence’的缩写)).
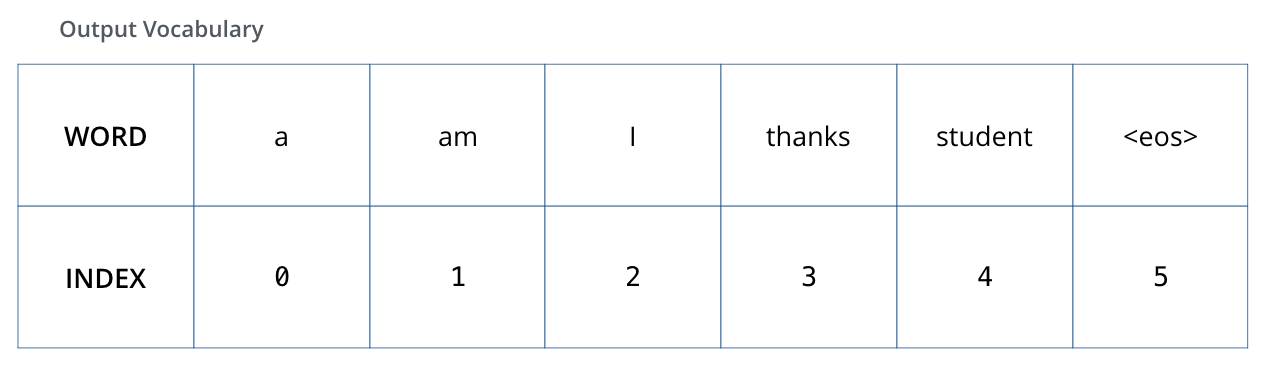
一旦定义了输出词汇表,就可以使用相同宽度的向量来表示词汇表中的每一个单词,也叫one-hot编码。例如我们可以用下面这个向量表示单词‘am’
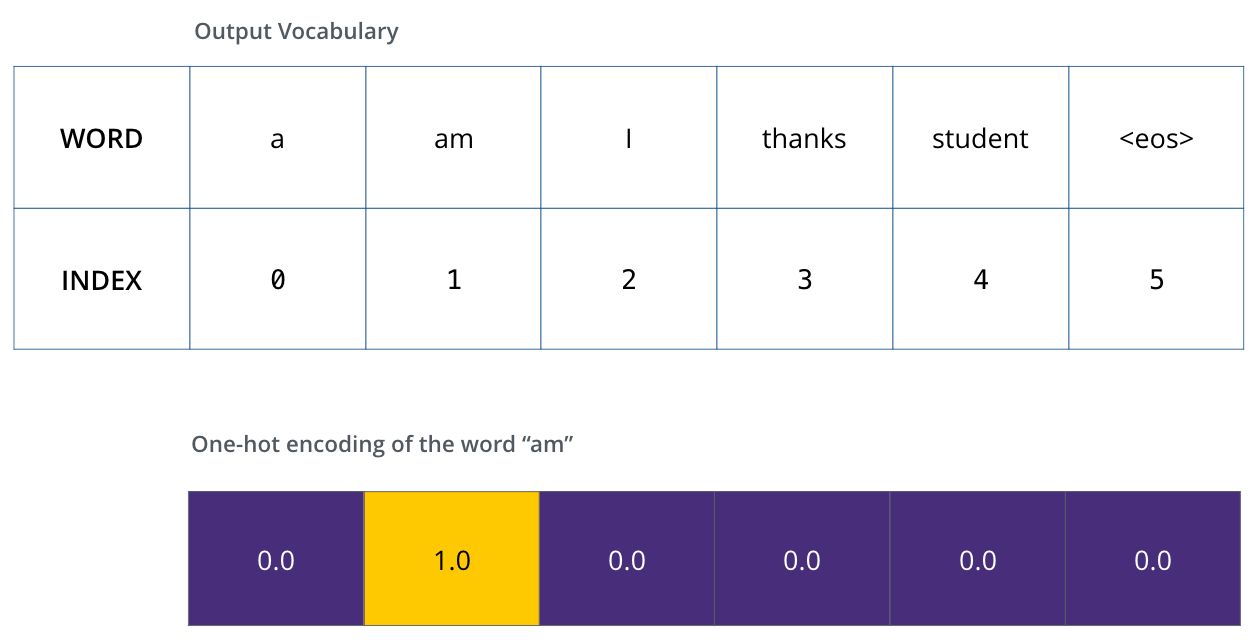
损失函数
假设我们正在训练我们的模型。第一步,我们先用一个简单的栗子迅联它——将‘merci’翻译成‘thanks’。
这就意味着我们要将thanks的概率放到最大,由于模型还没有被训练,显然这个方法不太可行。
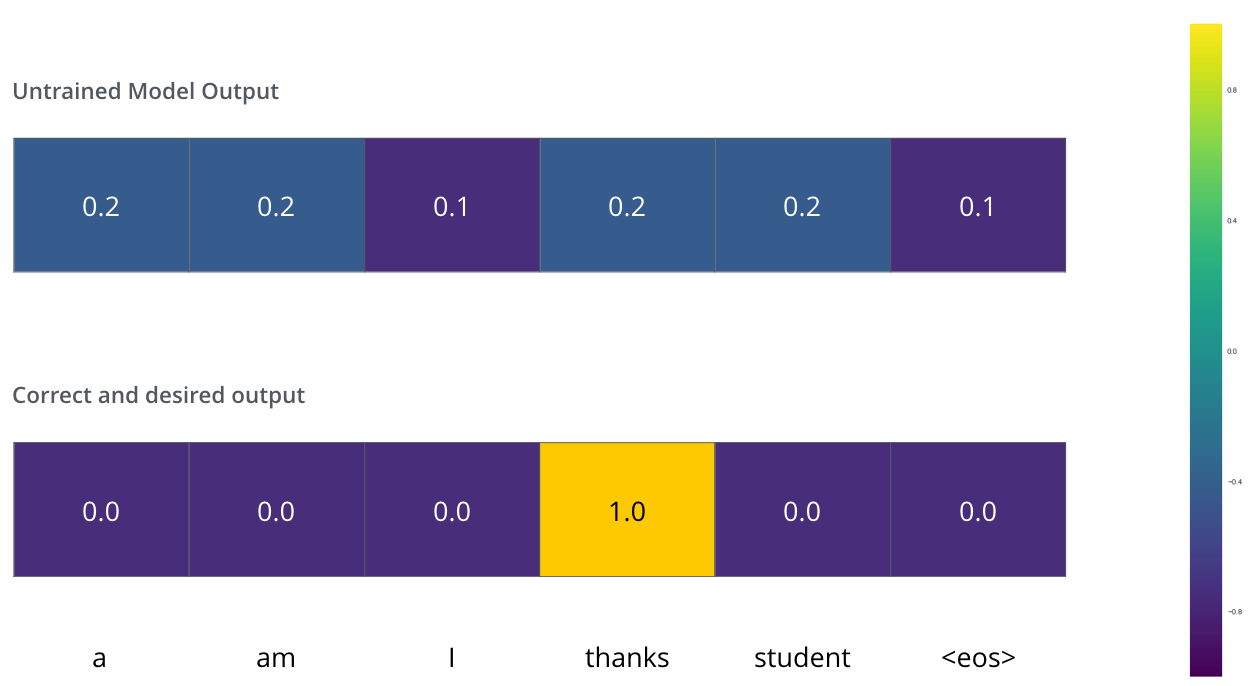
如何比较两个概率?我们只是简单的用一个减去另一个。要了解更多细节,查看交叉熵。
但是请注意,这是一个过于简化的例子。实际上,我们输入的是一个句子,而不是一个单词(当然输出也是句子)。例如输入:“je suis etudiant”,预期输出:“i am a student”。这意味着我们需要我们的模型输出连续的概率分布:
每个概率分布宽度为词汇大小(本例中为6)。
第一个概率分布I最高(也就是会输出I)。
第二个分布在am上最高(也就是会输出am)。
以此类推,最后一个输出<end of sentence>。
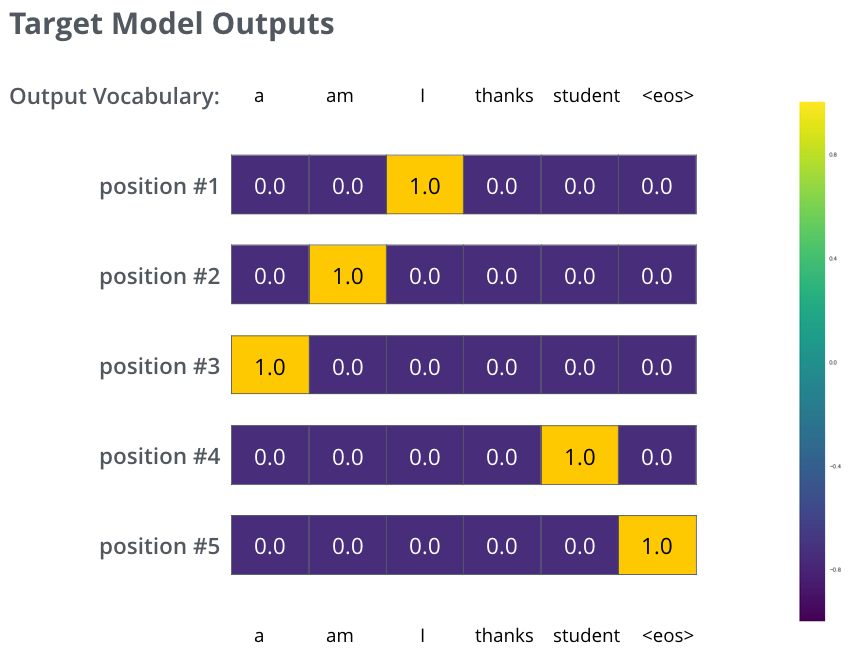
在一个足够大的数据集上对模型进行足够长实践的训练之后,我们获得的概率分布可能是这样的:
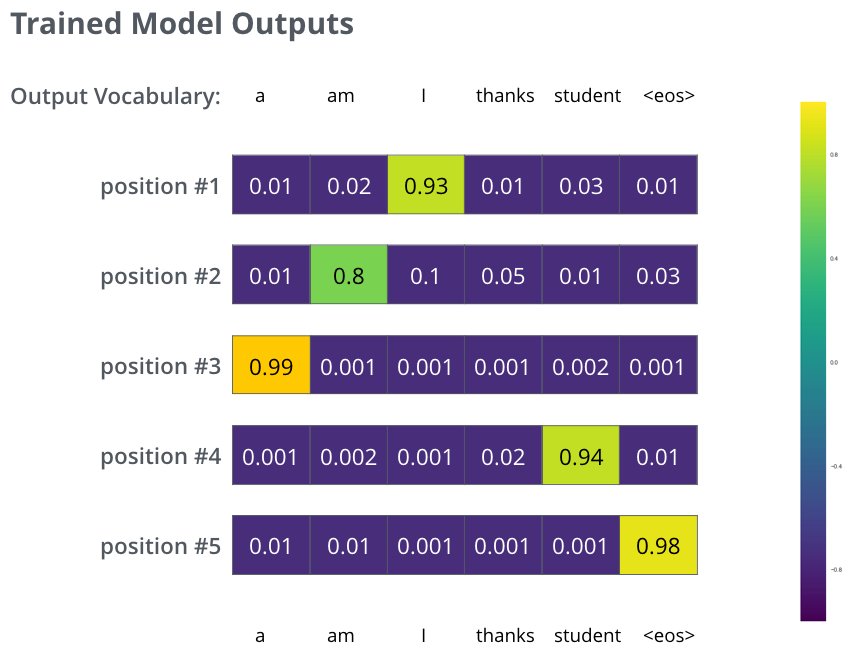
现在,因为这个模型每次产生一个输出,我们可以假设这个模型从概率分布中选择出了最高的概率然后丢弃掉其余的单词,这是一种贪心解法。
另一种方法是试图寻找全局最优解的方法叫beam search。
翻译整理自,Jay Alamar,The Illustrated Transforme
0 条评论