
1.1 插入排序
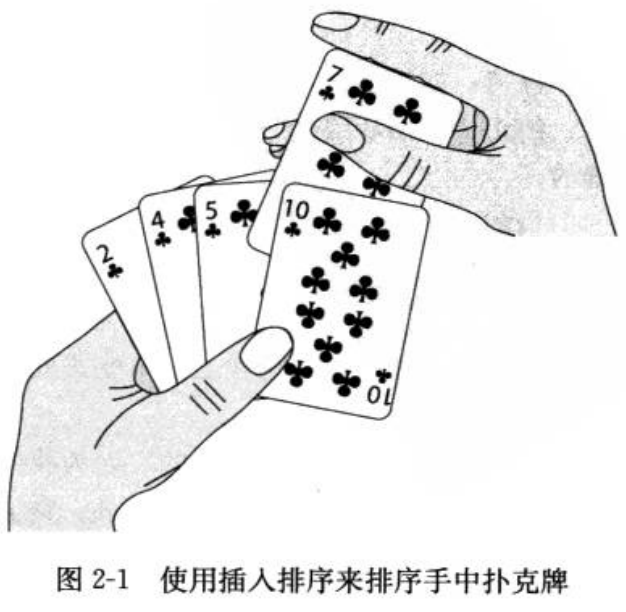
下图为排序中的几组中间状态,代码下面有,
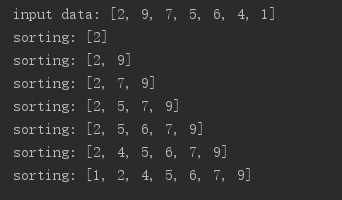
伪码:

python代码实现:
# -*- coding:utf-8 -*-
class InsertionSort:
def __init__(self):
pass
def sort(self, data):
"""
插入排序
:param data:排序列表
:return:
"""
print('input data:', data)
# 排序列表的长度
input_length = len(data)
# 遍历数据,可以从1开始,也可以从0,因为只有一个数的状态已经排好序,为了方便输出,这里写0
for i in range(0, input_length):
# 设置标记,保存当前排序的数
key = data[i]
# 计算需要比较的最大次数(只须向前比较即可,因此为i-1)
j = i - 1
# 从后向前遍历列表,直至标记比当前数大为止
while j >= 0 and data[j] > key:
# 如果当前数没有标记大,则当前数向后移
data[j + 1] = data[j]
# 向前查找遍历
j -= 1
# 将查找失败(j为第一个没有标记大的数字,所以标记应该在j+1的位置)
data[j + 1] = key
# 输出排序中间步骤,i+1是因为[]区间为左闭右开。
print('sorting:', data[:i + 1])
if __name__ == '__main__':
InsertionSort().sort([2, 9, 7, 5, 6, 4, 1])
1.2 分析算法
一般来说,算法需要的时间与输入的规模同步增长,所以通常把一个程序的运行时间描述成其输入规模的函数。 为此,我们必须更仔细地定义术语“运行时间”和“输入规模”。
输入规模的最佳感念依赖于研究的问题。对许多问题,如排序或计算离散傅里叶变换,最自然的度量是输入中的项数(排序数组长度n)。但是有时需要用两个数来描述输入规模更为合适,例如输入的是图,那么用定点数量和边数量来作为输入规模则更为合适。
运行时间是指算法执行的基本操作数或步数。定义“步”的概念以便尽量独立于机器是方便的。
对于上边插入排序的伪码,有代价

因此这个算法的执行总时长为:
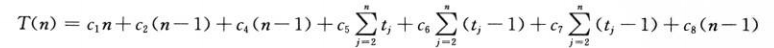
很显然,这个值与初始数据的排序有关,那么就有最坏情况、最好情况与平均情况分析。
对于最坏情况,即对规模为n的任何输入,算法的最长运行时间(也是最常使用的,理由如下)。
- 一个算法的最坏情况运行时间给出了任何输入的运行时间的一个上界。知道了这个上界,就能确保该算法觉不需要更长的时间。
- 对某些算法,最坏情况经常出现。
- “平均情况”往往与最坏情况大致一样差。
1.3 设计算法
1.3.1 分治法
许多有用的算法在结构上是递归的:为了解决一个给定的问题,算法一次或多次递归地调用其自身以解决紧密相关的若干子问题。这些算法典型地遵循分治法的思想:将问题分解为几个较小但类似于原问题的子问题,递归地求解这些子问题,然后再合并这些子问题的解来建立原问题的解。
分治模型在每层递归时都有三个步骤:
- 分解原问题为若干子问题,这些子问题是原问题的规模较小的实例。
- 解决这些子问题,递归地求解各子问题。
- 合并这些子问题的解成原问题的解。
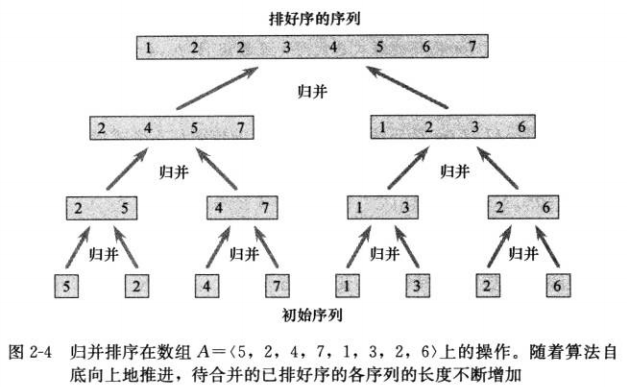
1.3.2 分析分治算法
当一个算法包含对其自身的递归调用时,我们往往可以用递归方程或递归式来描述其运行时间,该方程根据在较小输入上的运行时间来描述在规模为n的问题上的总运行时间。然后我们可以使用数学工具来求解递归式并给出算法性能的届。
我们可以将实际问题分解成一颗描述递归式的等价树,即递归树。
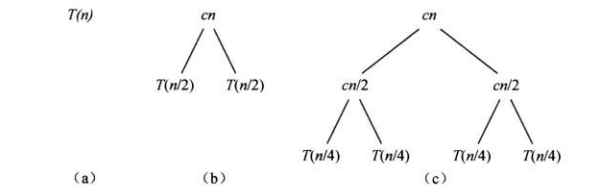
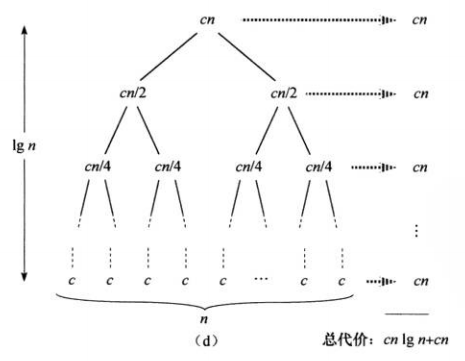
使用递归树计算时间复杂度:
练习2.3-3


练习2.3-4


练习2.3-7


0 条评论