【算法导论】单源最短路径

单源最短路径：给定一个图，我们希望找到从定源节点s到每个结点v的最短路径。

松弛操作：本章的算法需要使用松弛技术，对于每一个点，我们多维护一个变量d，用来记录从源节点到结点v的最短路的权重上界（也就是类似于多一个变量用来保存遍历到当前情况下到该结点的最短距离），我们称d为s到v的最短路径估计。

1.Bellman-Ford算法

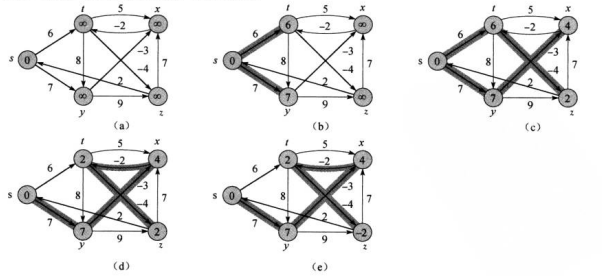
Bellman-Ford算法解决的是一般情况下的单源最短路径问题，在这里，边的权重可以为负值。

Bellman-Ford算法返回一个布尔值，以表明是否存在一个从源节点可以到达的权重为负值的环路（就是一个环路的总代价为负数）。如果存在这样一个环路，算法将告诉我们不存在解决方案。如果没有这种环路存在，算法将给出最短路径和他们的权重。

Bellman-Ford 算法引入了一个松弛操作用来检查是否存在负值环路。

def bellman_ford(self, graph):
    """
    bellman_ford算法(默认从0开始
    :param graph:
    :return:
    """
    weight = [float('inf') for _ in range(len(graph))]
    weight[0] = 0
    # 向前寻找并修改松弛变量
    for k in range(len(graph) - 1):
        for i in range(len(graph)):
            for j in range(len(graph[0])):
                if graph[i][j] != 0:
                    if weight[j] > weight[i] + graph[i][j]:
                        weight[j] = weight[i] + graph[i][j]
    # 再遍历一遍判断是否有负环路（有的话再来一遍代价必然会更低）
    for i in range(len(graph)):
        for j in range(len(graph[0])):
            if graph[i][j] != 0:
                if weight[j] > weight[i] + graph[i][j]:
                    return False
    return weight

2.Dijsktra算法

Dijkstra算法解决的是带权重的有向图上单源最短路径的问题，该算法要求所有边的权重都为非负值。时间复杂度O(V^2+E)=O(V^2)。

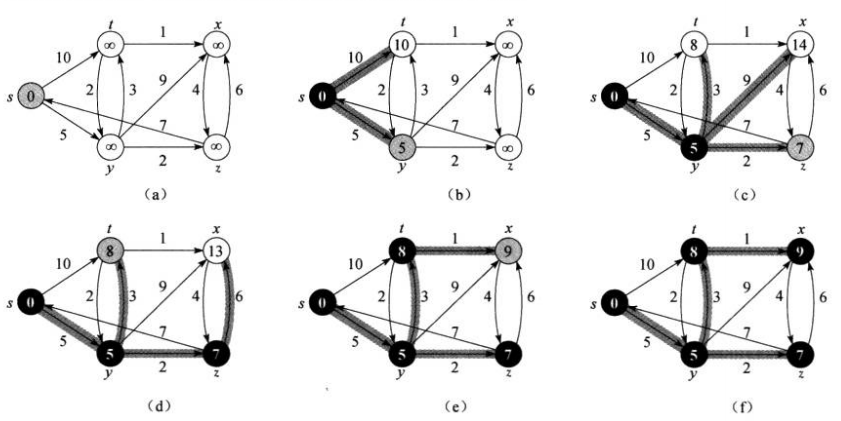
Dijsktra每次都贪心的获取当前状态下的最小距离作为下一次计算的基准。

def Dijsktra(self, graph):
    """
    Dijsktra算法(默认从0开始
    :param graph:
    :return:
    """
    weight = []
    # 初始化距离向量（因为调用的时候吧0作为inf了，这里需要处理一下x）
    for i in range(len(graph[0])):
        if graph[0][i] != 0:
            weight.append(graph[0][i])
        else:
            weight.append(float('inf'))
    # 访问列表
    vis = [0 for _ in range(len(graph))]
    vis[0] = 1
    weight[0] = 0
    # 查找最短路
    while sum(vis) != len(graph[0]):
        min_value = float('inf')
        min_index = 0
        # 寻找未被访问过的最小点
        for j in range(len(graph[0])):
            if weight[j] < min_value and vis[j] == 0:
                min_value = weight[j]
                min_index = j
        vis[min_index] = 1
        # 更新距离
        for j in range(len(graph[0])):
            if weight[j] > weight[min_index] + graph[min_index][j]:
                weight[j] = weight[min_index] + graph[min_index][j]
    return weight

事实上，我们可以优化Dijsktra到的复杂度到 O(V*lgV+E)，方法是使用斐波那契堆，改善的是每次寻找最小值的过程，将复杂度从V降为lgV。

3.差分约束和最短路径

差分约束系统

假如以下方程组：

我们可以整理出如下不等式组：

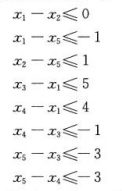
对于该组不等式，我们可以接触多个解。

这种就叫做差分约束系统，比如在x1时刻进行一个工作，必须在n个小时后进行下一个后置工作x2，因此就有约束x2-x1>=n。

约束图

对于上述不等式组，我们可以画出如下的图：

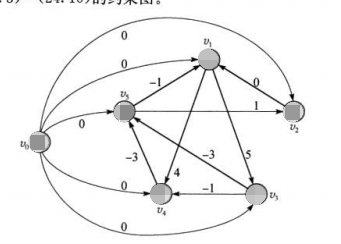
其中边即为不等式的右边。

求解差分约束系统

对于上图，很明显我们需要使用bellman-ford算法来解决（因为出现了负边）。