【算法导论】所有结点对的最短路径问题

（多源最短路径问题）

在本章中，我们考虑如何找到一个图中所有结点之间的最短路径，该问题在计算所有城市之间的交通道路距离时常出现。

我们当然可以运行n次基于贪心的单源最短路径来计算出结果，本章也介绍了一个基于动态规划算法来解决最短路径问题。

1.Floyd-Warshall算法

时间复杂度O(n^3)。

最短路径的结构

如果一条路径是最短路，那么这条路径的任何子路径依然是最短路。所以利用这条我们可以找到动态规划的最优子结构。

所有结点对最短路径问题的递归解

因此我们可以设计出如下递归定义：

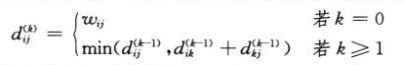
初始化为w_ij，之后都进行松弛操作。

自底向上计算最短路径权重

中间矩阵：

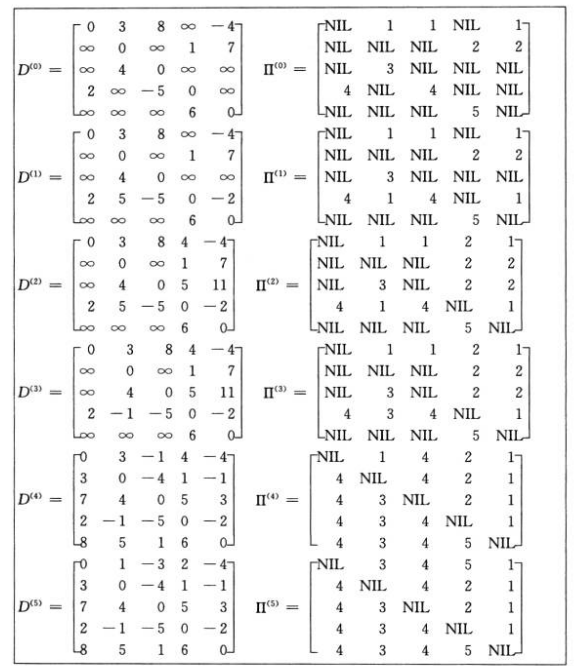
代码：

def floyd_warshall(self, graph):
    """
    floyd_warshall算法实现，其中graph就是weight
    :param graph: 
    :return: 
    """
    inf = float('inf')
    # 初始化path
    path = [[inf for _ in range(len(graph[0]))] for _ in range(len(graph))]
    for i in range(len(path)):
        for j in range(len(path[0])):
            if graph[i][j] != inf and i != j:
                path[i][j] = i
    for k in range(len(graph)):
        for i in range(len(graph)):
            for j in range(len(graph[0])):
                if graph[i][j] > graph[i][k] + graph[k][j]:
                    graph[i][j] = graph[i][k] + graph[k][j]
                    path[i][j] = k
    return graph, path

构建一条最短路径

需要注意，上述代码最终结果与上图并不完全一致

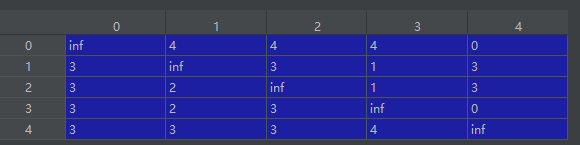
观察在（0，2）、（1，5）、（4，2）位置均不一样，上图为起始点第二个点的索引，而我的代码是终点前第一个点的所有（即真实路径一个正序输出一个倒序输出，这么做的目的是代码简单）。

2.用于稀疏图的Johnson算法

上述Floyd算法的时间复杂度为O(n^3)，当用于稀疏图的时候代价未免过大，本节介绍的Johnson算法的时间复杂度为O(V^2lgV+VE)的算法。

Johnson 算法使用的技术称为重新赋予权重。什么是重新赋予权重呢，字面意思就是重新赋予边的权重。

那么这个算法是什么样子呢？说出来你可能不信，就是进行n次Dijsktra算法（那么为什么是lgV呢，当然是使用改进的Dijsktra，选择的时间由V降为lgV），因为每次Dijsktra结果都会修改当前结点到其他结点的距离，下次计算时，我们就使用上一次的结果作为输入，因此叫重新赋予权重。