【算法导论】最大流

正如可以通过将道路交通图模型化为有向图来找到从一个城市到另一个城市之间的最短路径，我们也可以将一个有向图看作是一个“流网络”并使用它来解决关于物料流动方面的问题。

我们把流网络中每条有向边看作是物料流动的通道，是物料流经该通道的最大速率，我们希望计算从源节点运行物料到某个点的最大速率，这是流网络有关的所有问题中最简单的问题之一。

1.流网络

如下图即为s->t的最大流网络（需要注意，b图表示 当前流量/最大流量，并不代表除法）。

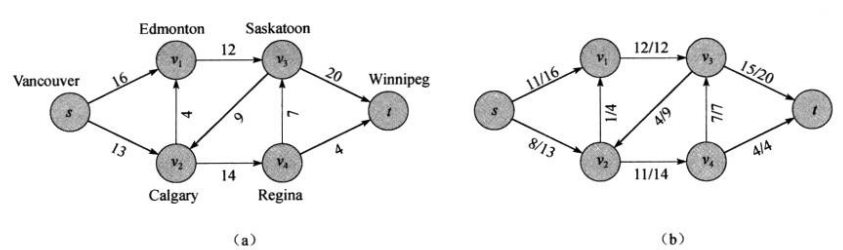
使用反平行边来模拟问题

对于有双向边的情况，我们使用一个虚拟结点来模拟该问题

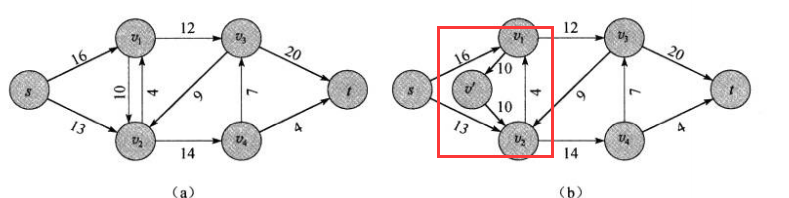
具有多个源结点和多个汇点的网络

一个最大流问题可能有几个源结点和几个汇点（终点）。

在具有多个源节点和多个汇点的网络中，我们添加一个超级源结点和一个超级汇点，它们分别连接着各个源节点和各个汇点。

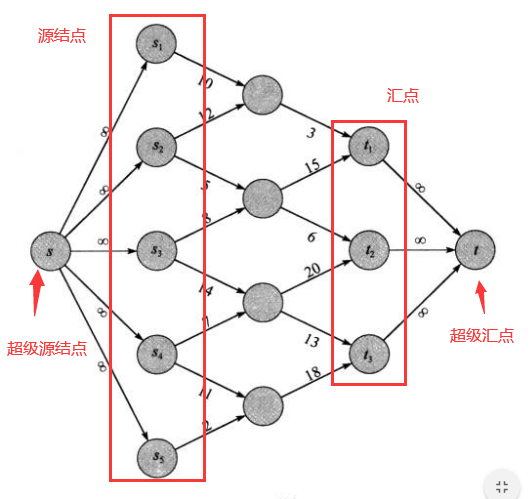
2.Ford-Fulkerson方法

本节讨论用来解决最大流问题的Ford-Fullkerson方法。之所以称其为方法而不是算法，是因为 Ford-Fullkerson 包含了几种运行时间各不相同的具体实现。

在这之前先解释几个概念

残存网络

一个显示管道还有多少剩余能力的网络，同时为了方便计算，还有一条相反的边用来记录反向剩余多少，比如点i到点j总能力20的管道，使用了15，则i->j为15，j->i为5。

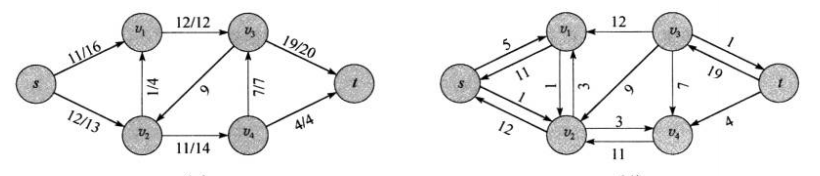
增广路径

增广路径为残存网络上一条可以从结点通往汇点的一条路径。

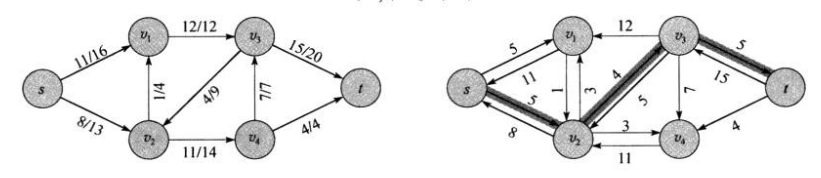
这条路上最小的残存容量是4，我们称一条增广路径p上能够为每条边增加的流量的最大值为路径p的残存容量。

基本的Ford-Fulkerson算法

在Ford-Fulkerson方法的每次迭代中，寻找某条增广路径p，然后使用p来对流f进行修改。

我们从残存网络中寻找一条增广路经，然后在流网络中增加或减少（增加或减少基于增广路径的边是不是源网络中的边，因为残存网络是双向边）增广矩阵的残存容量，直至残存网络中没有增广矩阵为止，则流网络即为最大流网络。

代码（由于这段使用了networkx来进行图运算，所以上完整代码）：

# -*- coding:utf-8 -*-
import networkx as nx
import matplotlib.pyplot as plt


class FordFulkerson():
    def __init__(self):
        self.inf = float('inf')
        pass

    def ford_fulkerson_method(self, flowGraph, remainGraph, from_node, to_node):
        while nx.has_path(remainGraph, from_node, to_node):
            # 寻找路径p的最小权重
            path = nx.shortest_path(remainGraph, from_node, to_node)
            min_weight = float('inf')
            min_weight_idx = 0
            for i in range(1, len(path)):
                if min_weight > remainGraph[path[i - 1]][path[i]]['weight']:
                    min_weight = remainGraph[path[i - 1]][path[i]]['weight']
                    min_weight_idx = i

            def judge_in_graph(G, from_node, to_node):
                for n, nbrs in G.adjacency():
                    for nbr, eattr in nbrs.items():
                        data = eattr['weight']
                        if n is from_node and nbr is to_node:
                            return True
                return False

            # 所有残存网络路径减（加）去最小值，流网络加（减）上最小值
            for i in range(1, len(path)):
                if judge_in_graph(flowGraph, path[i - 1], path[i]):
                    if remainGraph[path[i - 1]][path[i]]['weight'] - min_weight == 0:
                        remainGraph.remove_edge(path[i - 1], path[i])
                    else:
                        remainGraph[path[i - 1]][path[i]]['weight'] -= min_weight
                    flowGraph[path[i - 1]][path[i]]['weight'] += min_weight
                else:
                    if judge_in_graph(remainGraph, path[i - 1], path[i]):
                        remainGraph[path[i - 1]][path[i]]['weight'] -= min_weight
                    else:
                        remainGraph.add_edge(path[i - 1], path[i], weight=min_weight)
                    flowGraph[path[i - 1]][path[i]]['weight'] -= min_weight

        return flowGraph, remainGraph


if __name__ == '__main__':
    # 流图
    flowGraph = nx.DiGraph()
    flowGraph.add_nodes_from(['s', 'a', 'b', 'c', 'd', 't'])
    flowGraph.add_edges_from(
        [('s', 'a', {'weight': 0}), ('s', 'd', {'weight': 0}), ('a', 'b', {'weight': 0}),
         ('b', 't', {'weight': 0}),
         ('d', 'c', {'weight': 0}), ('c', 'b', {'weight': 0}), ('b', 'd', {'weight': 0}),
         ('c', 't', {'weight': 0}),
         ('d', 'a', {'weight': 0})])

    # 残存网络
    remainGraph = nx.DiGraph()
    remainGraph.add_nodes_from(['s', 'a', 'b', 'c', 'd', 't'])
    # remainGraph.add_edges_from(
    #     [('s', 'a', {'weight': 16}), ('a', 's', {'weight': 0}), ('s', 'd', {'weight': 13}),
    #      ('d', 's', {'weight': 0}),
    #      ('a', 'b', {'weight': 12}), ('b', 'a', {'weight': 0}), ('b', 't', {'weight': 20}),
    #      ('t', 'b', {'weight': 0}),
    #      ('d', 'c', {'weight': 14}), ('c', 'd', {'weight': 0}), ('c', 'b', {'weight': 7}),
    #      ('b', 'c', {'weight': 0}),
    #      ('b', 'd', {'weight': 9}), ('d', 'b', {'weight': 0}), ('c', 't', {'weight': 4}),
    #      ('t', 'c', {'weight': 0}),
    #      ('d', 'a', {'weight': 4}), ('a', 'd', {'weight': 0})])

    remainGraph.add_edges_from(
        [('s', 'a', {'weight': 16}), ('s', 'd', {'weight': 13}),
         ('a', 'b', {'weight': 12}), ('b', 't', {'weight': 20}),
         ('d', 'c', {'weight': 14}), ('c', 'b', {'weight': 7}),
         ('b', 'd', {'weight': 9}), ('c', 't', {'weight': 4}),
         ('d', 'a', {'weight': 4})])

    aaa = nx.shortest_path(flowGraph, 's', 't')
    print(aaa[1])
    print(type(aaa[1]))
    # print(nx.shortest_path(flowGraph, 's', 't'))
    print(flowGraph['s'][aaa[1]]['weight'])
    # remainGraph.add_edge('s', 'e', weight=10)
    print(FordFulkerson().ford_fulkerson_method(flowGraph, remainGraph, 's', 't'))
    # nx.shortest_path()
    # nx.draw(remainGraph)
    # plt.show()

最后可以算出结果：

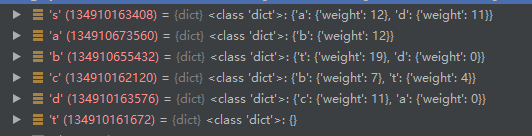
因此，最优的这条管道体系 最多输送s的出度权重——12+11=23个单位的货物。

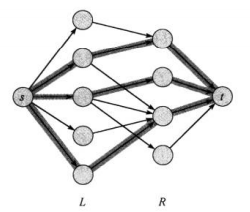
3.最大二分匹配

最大二分匹配是在图中找到最大的二分匹配项。

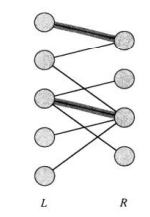
如图，为基数为2的最大匹配

基数为3的最大匹配

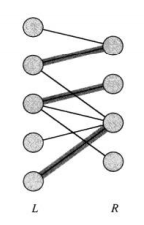
因此对于这类问题，我们可以转换成最大流算法，添加一个超级源结点和超级汇点并赋予每条边的权重为1，我们就可以将问题转换为最大流问题。