
在分治策略中,我们递归地求解一个问题,在每层递归中使用如下三个步骤:
- 分解(Divide)步骤将问题划分为一些子问题,子问题的形式与原问题一样,只是规模更小。
- 解决(Conquer)步骤递归地求解出子问题,如果问题的规模足够小,则停止递归,直接求解。
- 合并(Combine)步骤将子问题的解组合成原问题的解。
当子问题足够大时,我们称之为递归情况,当问题足够小时,我们称为进入了基本情况。
递归式是一个等式或不等式,它通过更小的输入上的函数值来描述一个函数,如下。
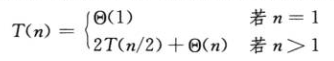
1.最大子数组问题
获取一个数组中最大子序列的问题,我们可以用暴力求解法,这样的时间复杂度是n^2。

那我们可以使用别的方法,取当前数组的一个中间值,那么最大子数组就有且仅有三种可能,即跨越中点,中点以左和中点以右。

那么我们就可以将问题进一步的划分,在中间点左右的两种情况下,我们依然可以认为是跨越中点的,因为我们可以截取数组长度来“移动”这个中点,因此我们只需要在中点左右分别计算最大子数组,合起来就是跨越当前中点的最大子数组,然后二分地移动中点,我们就可以计算其他的当前最大子数组,当我们使用二分遍历完成所有的“中点”后便可以找到整个数组长度下的最大子数组。而这种算法的时间复杂度只有n`lgn。
代码求解最大子数组以及子数组和。

代码:
# -*- coding:utf-8 -*-
class FIndMaxSubarray:
def __init__(self, init_array):
self.init_array = init_array
pass
def find(self, start, end):
"""
递归寻找最大子数组
:return:
"""
# 递归结束标记
if start == end:
return [self.init_array[start]], self.init_array[start]
mid = int((start + end) / 2)
# 分别处理左、右、以及跨越重点的情况
left_subarray, left_sum = self.find(start, mid)
right_subarray, right_sum = self.find(mid + 1, end)
cross_subarray, cross_sum = self.find_max_crossing_subarray(target_array=self.init_array[start:end+1])
# 比较三种结果大小并返回
if left_sum >= right_sum and left_sum >= cross_sum:
return left_subarray, left_sum
elif right_sum >= left_sum and right_sum >= cross_sum:
return right_subarray, right_sum
else:
return cross_subarray, cross_sum
def find_max_crossing_subarray(self, target_array):
"""
寻找当前列表以中点为基准的最大子列表
:param target_array:
:return:
"""
# 左最大子数组
left_max_sub_array = []
# 右最大子数组
right_max_sub_array = []
# 中间索引
mid_index = int(len(target_array) / 2)
# 最大子数组
max_subarray = []
# 中间值
mid_number = target_array[mid_index]
# 临时存储的最大值
_sum = 0
# 临时存储的索引值
_index = 0
# 用于存放临时和的变量
temp_sum = 0
# 对左侧数字查找最大子数组
for i in range(mid_index, 0, -1):
# 计算临时和
temp_sum = temp_sum + target_array[i]
# 判断该位取舍
if temp_sum > _sum:
_sum = temp_sum
_index = i
# 截取数组
left_max_sub_array = target_array[_index:mid_index]
# 数据初始化
_sum = 0
_index = 0
temp_sum = 0
# 对右侧数字查找最大子数组
for i in range(mid_index, len(target_array)):
temp_sum = temp_sum + target_array[i]
if temp_sum > _sum:
_sum = temp_sum
_index = i
# 截取数组
right_max_sub_array = target_array[mid_index:_index + 1]
# 合并数组
max_subarray = left_max_sub_array + right_max_sub_array
# 求和
max_subarray_sum = sum(max_subarray)
return max_subarray, max_subarray_sum
if __name__ == '__main__':
init_array = [13, -3, -25, 20, -3, -16, -23, 18, 20, -7, 12, -5, -22, 15, -4, 7]
max_sum, max_array = FIndMaxSubarray(init_array).find(0, len(init_array) - 1)
print(init_array)
print(max_array, '\t', max_sum)
pass
2.用代入法求解递归式
例练习4.3-6,类似于数学归纳法,首先假设一个时间复杂度,然后代入递归式验证猜想是否成立。
需要注意,有的时候需要使用一些小技巧,包括合理的猜测,微妙的细节以及改变变量(类似于高数中的换元,例4.3-9)
3.用递归树方法求解递归式
例练习4.4-6,首先根据递归式画出递归树,然后根据递归树写出时间复杂度。
4.用书方法求解递归式
例练习4.5.1,通式
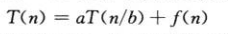
对于该通式有
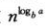
然后判断f(n)和上式的大小,则作为T(n)的时间复杂度。
练习4.3-6
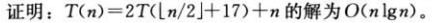

练习4.3-9
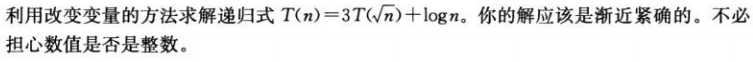

练习4.4-6

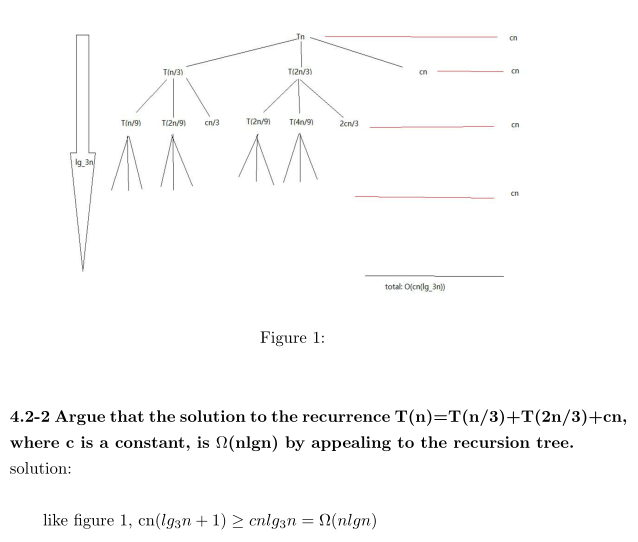
练习4.4-9


练习4.5-1


0 条评论