【算法导论】快速排序

对于包含n个数的输入数组来说，快速排序是一种最快情况时间复杂度为O(n^2)的排序算法。虽然最坏情况时间复杂度很差，但是快速排序通常是实际排序应用中最好的选择，因为它的平均性能非常好，期望是O(nlgn)，而且 O(nlgn) 中隐含的常数因子非常小，并且具有原址性。

1.快速排序的描述

快速排序可以理解为选择一个基准，以这个基准将列表分为大于基准和小于基准的两部分，并类似二分法继续向下选择基准。

每一趟快速排序之后都有一个元素位于正确的位置。

简单的描述就是：从前向后找比基准大的并交换，从后向前找比基准小的并交换。

代码，时间复杂度O(n)：

def quick_sort(self, init_list, i):
    """
    快速排序
    :param init_list: 排序列表
    :param i: 比较元素索引
    :return:
    """
    length = len(init_list)
    # 计算左右索引
    left_index = 0
    right_index = length - 1
    # 将比较元素放到最后，防止它是最大值时不进行交换
    temp = init_list[i]
    init_list[i] = init_list[right_index]
    init_list[right_index] = temp
    # 比较元素值
    flag = init_list[right_index]
    # 比较元素索引（因为交换元素位置会变）
    flag_index = right_index
    # 重复执行直至左右标记重叠
    while left_index != right_index:
        # 从左向右找比flag大的数交换
        for i in range(left_index, right_index):
            if flag < init_list[left_index]:
                temp = flag
                init_list[flag_index] = init_list[left_index]
                flag_index = i
                init_list[left_index] = temp
                break
            else:
                left_index += 1
        # 从右向左找比flag小的数交换
        for i in range(right_index, left_index, -1):
            if flag > init_list[right_index]:
                temp = flag
                init_list[flag_index] = init_list[right_index]
                flag_index = i
                init_list[right_index] = temp
                break
            else:
                right_index -= 1
    return init_list

2.快速排序的性能

最坏情况划分

考虑一种情况：每次选择的基准都是当前序列中最小的序列，因此需要进行n次排序，每次排序代价是 O(n) ，因此最坏的时间复杂度是 O(n^2)。

最好情况划分

考虑一种情况：每次选择的基准都是当前序列中中间的数字，每次选择的基准正好将序列分成了一棵满二叉树，因此最好情况的时间复杂度为 O(nlgn)。

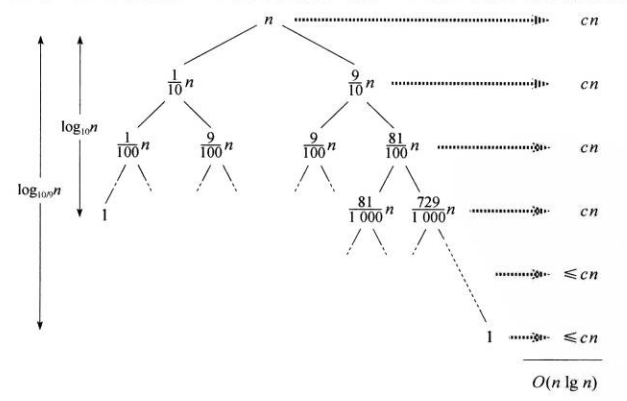
平衡的划分

即使是没有达到完美的1/2分，加入是9：1的区分，依然可以达到一个 O(nlgn)的时间复杂度。

3.快速排序的随机化版本

随机化的版本不再固定的选择某一个数，而是随机选择向下递归，因此我们需要稍微修改一下之前的快排代码，添加一个左右指针，指定本地递归需要排序的范围。

def quick_sort_for_random(self, init_list, i, left, right):
    """
    快速排序
    :param init_list: 排序列表
    :param i: 比较元素索引
    :return:
    """
    length = len(init_list)
    # 计算左右索引
    left_index = left
    right_index = right
    # 将比较元素放到最后，防止它是最大值时不进行交换
    temp = init_list[i]
    init_list[i] = init_list[right_index]
    init_list[right_index] = temp
    # 比较元素值
    flag = init_list[right_index]
    # 比较元素索引（因为交换元素位置会变）
    flag_index = right_index
    # 重复执行直至左右标记重叠
    while left_index != right_index:
        # 从左向右找比flag大的数交换
        for i in range(left_index, right_index):
            if flag < init_list[left_index]:
                temp = flag
                init_list[flag_index] = init_list[left_index]
                flag_index = i
                init_list[left_index] = temp
                break
            else:
                left_index += 1
        # 从右向左找比flag小的数交换
        for i in range(right_index, left_index, -1):
            if flag > init_list[right_index]:
                temp = flag
                init_list[flag_index] = init_list[right_index]
                flag_index = i
                init_list[right_index] = temp
                break
            else:
                right_index -= 1
    return init_list, left_index

然后是随机快排：

def random_quick_sort(self, init_list, left, right):

    """
    随机快速排序
    :param init_list:列表
    :return:
    """
    # 如果是单一元素排序，直接返回
    if right == left:
        return init_list
    # 随机初始化一个目标元素
    random_index = random.randint(left, right)
    # 进行排序，获取到排序后的列表以及目标元素现在的索引
    sort_list, sort_flag_index = self.quick_sort_for_random(init_list.copy(), random_index, left, right)
    # 如果当前目标不是最小值，则排序左子树
    if sort_flag_index != left:
        sort_list = self.random_quick_sort(sort_list, left, sort_flag_index - 1)
    # 如果当前目标不是最大值，排序右子树
    if sort_flag_index != right:
        sort_list = self.random_quick_sort(sort_list, sort_flag_index + 1, right)
    return sort_list

运行结果：