【算法导论】中位数和顺序统计量

中位数：分为上中位数和下中位数，上中位数即长度除2向上取整，下中位数为长度除2向下取整。一般说中位数默认下中位数。

顺序统计量：即第几小的数。一个数组的第一顺序统计量即为最小的数，第n顺序统计量即为最大的数。

1.最小值和最大值

如果我们要找出一个序列中的最小值，我们需要进行n-1次比较，同样，如果我们要找出一个序列中的最大值，也需要进行n-1次比较。

那如果我们需要同时找出最小值和最大值呢，那就需要2n-2次比较。

但是如果我们不再是用一个数与已经记录的最大最小值进行比较，而是用两个数先比较，然后取较小的一个和最大值比较，较大的和最大值比较，这样三次比较就可以完成两个数的比较，较上面的方法节约了一次比较，因而我们只需要

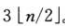
次比较即可。

2.期望为线性时间的选择算法

我们知道，快速排序的每一趟的结果，标记元素都会落在它最终结果的位置上，因此我们可以利用这个性质，达到以线性时间来寻找序列的顺序统计量。

def quick_sort(self, init_list, i, left, right):
    """
    快速排序
    :param init_list: 排序列表
    :param i: 比较元素索引
    :return:
    """
    length = len(init_list)
    # 计算左右索引
    left_index = left
    right_index = right
    # 将比较元素放到最后，防止它是最大值时不进行交换
    temp = init_list[i]
    init_list[i] = init_list[right_index]
    init_list[right_index] = temp
    # 比较元素值
    flag = init_list[right_index]
    # 比较元素索引（因为交换元素位置会变）
    flag_index = right_index
    # 重复执行直至左右标记重叠
    while left_index != right_index:
        # 从左向右找比flag大的数交换
        for i in range(left_index, right_index):
            if flag < init_list[left_index]:
                temp = flag
                init_list[flag_index] = init_list[left_index]
                flag_index = i
                init_list[left_index] = temp
                break
            else:
                left_index += 1
        # 从右向左找比flag小的数交换
        for i in range(right_index, left_index, -1):
            if flag > init_list[right_index]:
                temp = flag
                init_list[flag_index] = init_list[right_index]
                flag_index = i
                init_list[right_index] = temp
                break
            else:
                right_index -= 1
    return init_list, left_index
def randomized_select(self, init_list, order_statistic_idx, left, right):
    """
    利用快速排序找出第n个顺序统计量
    :param init_list:
    :param order_statistic_idx:
    :return:
    """
    if len(init_list) == 1:
        return init_list
    random_index = random.randint(left, right)
    init_list, flag_idx = self.quick_sort(init_list, random_index, left, right)
    # 这里进行了剪枝，不需要想快排一样左右均排序，选择一侧的进行排序即可
    if flag_idx == order_statistic_idx:
        return init_list[flag_idx]
    elif flag_idx > order_statistic_idx:
        return self.randomized_select(init_list, order_statistic_idx, left, flag_idx - 1)
    else:
        return self.randomized_select(init_list, order_statistic_idx, flag_idx + 1, right)

3.最坏情况为线性时间的选择算法

通过将序列分区排序查找中位数的操作来确定整个整个序列的（近似）中位数，然后利用这个中位数执行一趟快排，然后就和上面类似了。