1.直接寻址表
直接寻址法类似于标记数组,假定有一组序列的最大值为n,定义一个长度为n的零数组,如果序列中有数i,则数组第i个元素为1。
2.散列表
散列表则通过一个函数,将序列中的元素进行某种函数运算,映射到一个表中,我们将这种表称为散列表。
同时我们将数据长a和散列表长b的比值作为装载因子(a/b),这个值大于小于或者等于1均可。
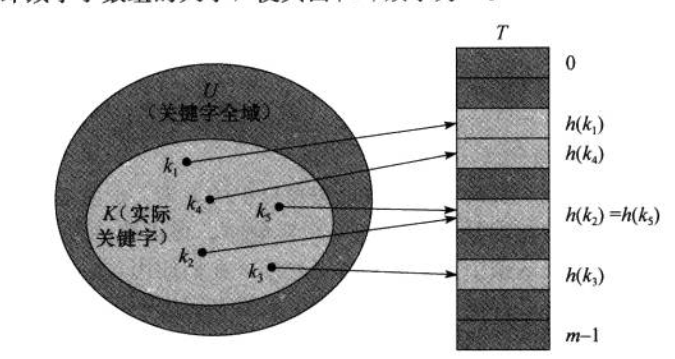
如果有两个实际关键字经过函数运算之后的值相同,那么我们称这种情况称为冲突。
我们有两种方法来解决这个冲突:开放寻址法和链接法。
通过链接法解决冲突:
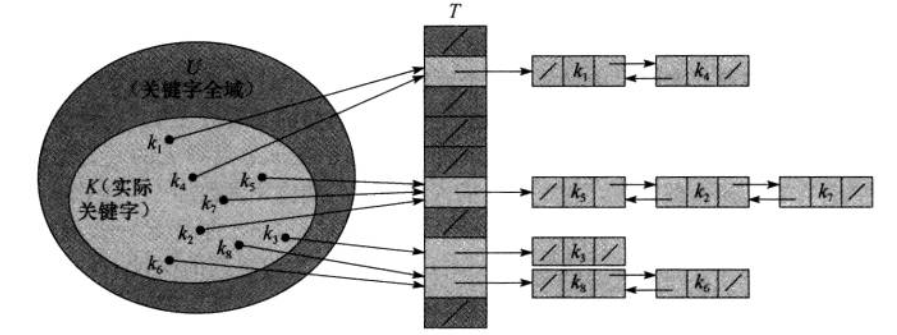
如下图,使用链表来作为存储元素的方式,比较建议使用双向链表,这样在删除元素的时候复杂度较低(最坏的情况下仍为O(1))。
3.散列函数
好的散列函数的特点
好的散列函数需要将各个元素映射到同一位置的概率尽可能低。
将关键字转换为自然数
除法散列法
对于实际关键字不是数字而是字母的情况,我们可以使用其ASCII码作为key来进行散列计算。
散列函数为:
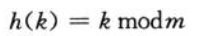
假如散列表长度为13,数据为100,因此计算结果为9,因此100在第九个位置。
乘法散列法
对于一些小数较多的序列,我们可以使用乘法散列表
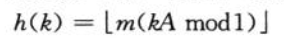
其中kA mod 1是k的小数部分。
全域散列法
上面的方法都会存在极端情况下冲突的次数为n,而全域散列法可以更好的避免这种情况。
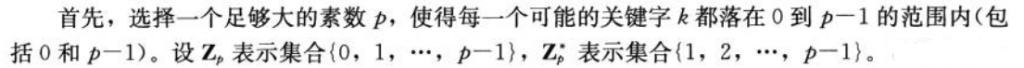

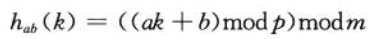
4.开放寻执法
开放寻执法的装载因子必须大于1。
如果发生冲突,将继续向下查找直至空位置。而向下找的方法又有三种:线性探测、二次探查和双重探查。
线性探测:
如果当前计算的位置被占用,则查看当前位置下一个位置,纸质第一个为空的位置,将该元素放入其中。
二次探测:
散列函数:
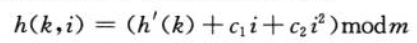
其实就是在一般的函数h(k)后面加上了一个二次函数,第一次我们尝试h(k),如果发生冲突,则根据后面的二次函数(i从1递增)来计算下一个映射值。
双重探查:
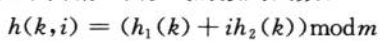
使用两个散列函数(而不是二次探测的二次方程)来多进行一次散列。
散列函数:
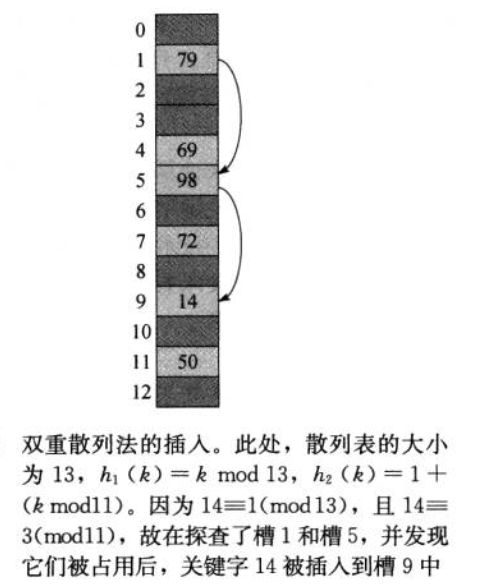
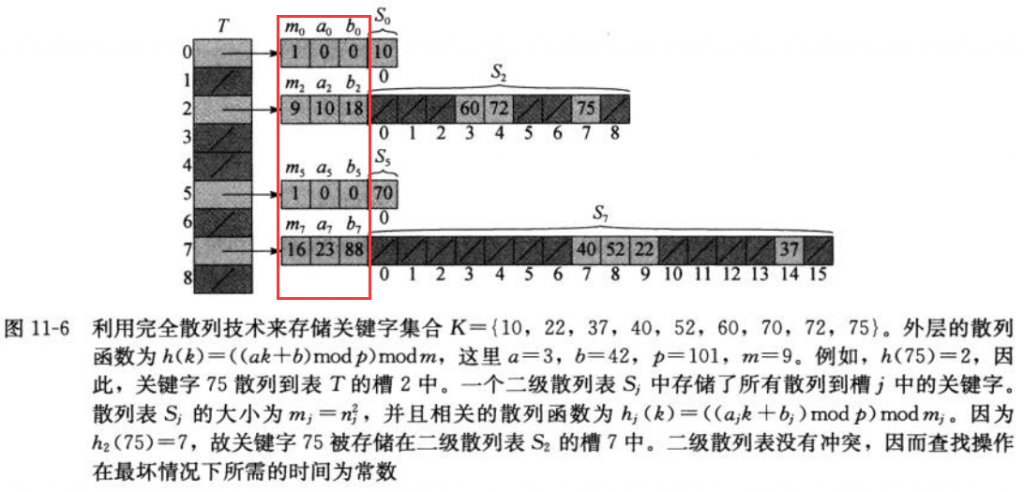
5.完全散列
完全散列使用了两次全域散列,栗子如下:
0 条评论