
1 雇佣问题
假如你要雇佣一名新的办公助理。你承诺在任何时候,都要找到最合适的人来担任这项任务,且只能有一个人被雇佣,当雇佣新的人时,之前的要解雇,同时还要支付给中介一大笔中介费。
我们假设面试的费用是c_i,雇佣的费用为c_h,下面看伪代码:

显然,在任何情况下都需要面试n次,而雇佣的次数越少,代价也就越低。
但是在最坏的情况下(受聘者能力依次递增),我们的代价依然很大,如果我们能尽量减少雇佣次数,那么我们的代价就会降低。
那么我们怎么避免有序的输入呢?那就是使用一个随机算法,将输入的序列打乱,避免输入有序。
2.指示器随机变量
我们引入一个概率与期望之间提供转换的一个便利的方法:指示器随机变量:

举个例子,我们来确定抛硬币时正面朝上的期望次数,正面朝上则值为1,否则为0。

因此正面朝上的期望次数就变成指示器的期望值:
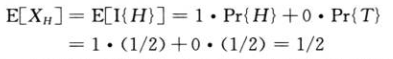
因此抛掷一枚硬币正面朝上的概率就是1/2。
2.1 用指示器随机变量分析雇佣问题
我们假设应聘者以随机的顺序出现,定义第i个应聘者被雇佣这个事件的指示器随机变量。
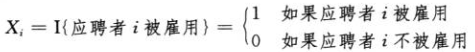
而X = X_1 + X_2 + … + X_n
因此X的期望:

因此,尽管我们面试了n个人,但是我们只雇佣其中lnn个人,代价显著下降。
3.随机算法
随机算法对于最坏输入,往往会破坏这种最坏的序列,产生一个较好的输入来改善算法,而对于一些已经很好的输入(如雇员问题中,输入递减,这种情况下只会雇佣一次),随机化之后则相对于原输入的代价更大。也就是说随机化并不一定能降低代价,只是即使最坏的输入也无法产生最大的代价,因为随机排列使得输入次序不再相关(除非随机数生成器产生一个“不走运”的排列)。
4.概率分析和指示器随机变量的进一步使用
4.1 生日悖论
Q:一个屋子要有多少人才能达到其中两人生日相同的机会达到50%?
我们假设:
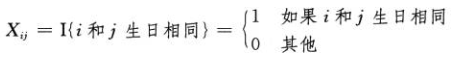
对于i和j在同一天过生日的概率(假设一年的天数为n):

那么相同的概率,需要再乘上一年的天数n:
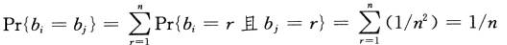
那么有:

计算期望:
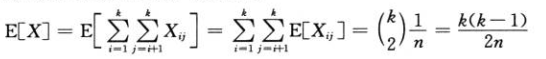
那么当我们期望为1/2时,我们计算k(k-1)=n,求解k约为28人。
0 条评论