【算法导论】线性时间排序

1 计数排序

计数排序假设n和输入元素中的每一个都是在0到k区间内的一个整数，其中k为某个整数。当k=O(n)时，排序的运行时间为Theta(n)。

计数排序的思想是每输入一个元素x，确定小于x的个数。利用这一信息，就可以直接把x放到它的输出数组中对应的位置了（当然在有重复数据的情况下要做一点修改）。

很显然，计数排序又一个缺点就是当需要排序的数值很大时，空间浪费非常大。而且不能排序非整数。

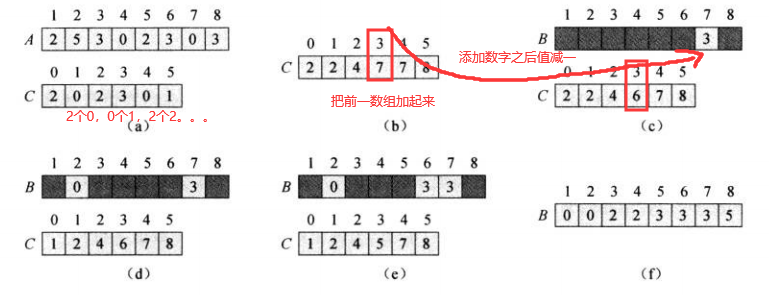
下面是伪码：

代码：

def count_sort(self, init_list):
    """
    计数排序
    :param init_list: 需要被排序的列表
    :return:
    """
    max_num = max(init_list)
    # 初始化辅助列表，为了对齐排序元素，0 index不用，所以+1
    assist_list = [0 for _ in range(max_num + 1)]
    # 计算元素个数
    for each in init_list:
        assist_list[each] += 1
    # 相加
    for i in range(len(assist_list) - 1):
        assist_list[i + 1] += assist_list[i]
    # 恢复init_list数组
    for i in range(len(assist_list) - 1, -1, -1):
        while assist_list[i] != 0:
            init_list[assist_list[i]-1] = i
            assist_list[i] -= 1
    return init_list

2.基数排序

基数排序通过对每一位进行排序从而完成整体的排序。

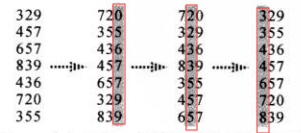
伪码：

代码：

def radix_sort(self, init_list):
    """
    基数排序
    :param init_list: 排序列表
    :return:
    """
    # 最大数字
    max_num = max(init_list)
    # 最大位数
    max_loop = len(str(max_num))
    # int 转 str并补零
    init_list_str = []
    for each in init_list:
        init_list_str.append(str(each).rjust(max_loop, '0'))
    # 获取x位的值并排序
    for i in range(max_loop - 1, -1, -1):
        sort_num = []
        # 获取位数
        for j in range(len(init_list)):
            sort_num.append(init_list_str[j][i])
        # 进行冒泡排序
        for ii in range(len(init_list_str)):
            for jj in range(ii, len(init_list_str)):
                if sort_num[ii] > sort_num[jj]:
                    # 交换sort_num以及init_list_str的值
                    temp = sort_num[ii]
                    sort_num[ii] = sort_num[jj]
                    sort_num[jj] = temp
                    temp = init_list_str[ii]
                    init_list_str[ii] = init_list_str[jj]
                    init_list_str[jj] = temp
    # str 转回 int
    return [int(i) for i in init_list_str]