【算法导论】二叉搜索树

1.什么是二叉搜索树

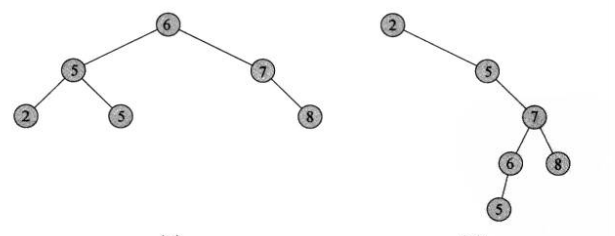
二叉搜索树：对任何结点x，其左子树中的关键字最大不超过x.key，其右子树的关键字最小不低于x.key，不同的二叉搜索树可以代表同一组值的集合。

二叉搜索树的性质允许我们通过一个简单的递归算法来按序输出二叉树中的所有关键字，这种算法称为中序遍历算法（左根右），类似的还有先序遍历（根左右）和后序遍历（左右根）。

2.查询二叉搜索树

查找

我们使用标准的链表存储树的方式，即left存储左孩子，right存储又孩子。

    def tree_search(self, root, k):
        """
        二叉树搜索
        :param k:搜索是否有k
        :return:
        """
       if root is None:
           return None
       if root.value == k:
           return root.value
       if k < root.value:
           return self.tree_search(root.left, k)
       else:
           return self.tree_search(root.right, k)
class Node():
    def __init__(self, value, left=None, right=None):
        self.value = value
        self.left = left
        self.right = right
    def getter_value(self):
        return self.value
    def getter_left(self):
        return self.left
    def getter_right(self):
        return self.right
    def setter_value(self, value):
        self.value = value
    def setter_left(self, left):
        self.left = left
    def setter_right(self, right):
        self.right = right

初始化树：

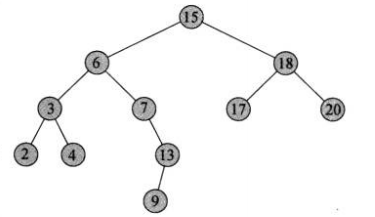
n11 = Node(9)
n10 = Node(13, n11)
n9 = Node(4)
n8 = Node(2)
n7 = Node(20)
n6 = Node(17)
n5 = Node(7, None, n10)
n4 = Node(3, n8, n9)
n3 = Node(18, n6, n7)
n2 = Node(6, n4, n5)
root = Node(15, n2, n3)
b = BinaryTree(root)

最大关键字元素和最小关键字元素

通过根节点，向左（右）寻找最左（右）的叶子节点，即为最小（大）关键字元素。

def tree_max(self):
    """
    搜索最大元素
    :return:
    """
    node = self.root
    while node.right is not None:
        node = node.right
    return node.value

def tree_min(self):
    """
    搜索最小元素
    :return:
    """
    node = self.root
    while node.left is not None:
        node = node.left
    return node.value

3.插入和删除

插入和删除操作会引起二叉搜索树表示的动态集合变化。因此一定要修改数据结构来反映这个变化，并且保持二叉搜索树的性质成立。

插入

结点插入要插入到一个插入后依然保持二叉搜索树性质的位置，找到后容然后交换。

这个想简单了哈哈哈哈后面红黑树插入的时候发现有情况没考虑到，这个有些情况会出现异常，我把后面红黑树的插入放过来，不涉及红黑树变换，除了多了个指针没区别。

这是错误代码：

def tree_insert(self, node, k, pre=None, left=True):
    """
    插入树
    :param node: 根节点
    :param k: 插入值
    :param pre: 当前节点的父节点
    :param left: 是否为向左寻找（判断大小的依据）
    :return:
    """
    # 说明需要新增叶子节点
    if node is None:
        n = Node(k)
        if left:
            pre.left = n
        else:
            pre.right = n
        return
    # 向左比较
    if node.value > k and left:
        self.tree_insert(node.left, k, node, True)
    # 向右比较
    elif node.value < k and not left:
        self.tree_insert(node.right, k, node, False)
    # 插入结点
    else:
        n = Node(k)
        if left:
            pre.left = n
            n.left = node
        else:
            pre.right = n
            n.right = node

红黑树部分的插入（不涉及旋转变化）：

def rb_insert(self, node, k, pre=None, left=True):
    """
    插入树
    :param node: 根节点
    :param k: 插入值
    :param pre: 当前节点的父节点
    :param left: 是否为向左寻找（判断大小的依据）
    :return:
    """
    print(node.key)
    # 说明需要新增叶子节点
    if node.left.key == None or node.right.key == None:
        print('leave')
        n = Node(k, 'red')
        if node.key > k:
            node.left = n
            n.pre = node
            n.left = n.right = self.root.pre
        else:
            node.right = n
            n.pre = node
            n.right = n.left = self.root.pre
        # self.rb_fixup(n)
        return
    # 向左比较
    if node.key > k and left:
        self.rb_insert(node.left, k, node)
    # 向右比较
    elif node.key < k:
        self.rb_insert(node.right, k, node)
    # 插入结点
    else:
        n = Node(k, 'red')
        if left:
            pre.left = n
            n.pre = pre
            n.left = node
            node.pre = n
            n.right = node.right
            node.right.pre = n
            node.right = self.root.pre
        else:
            pre.right = n
            n.pre = pre
            n.right = node
            node.pre = n
            n.left = node.left
            node.left.pre = n
            node.left = self.root.pre

删除

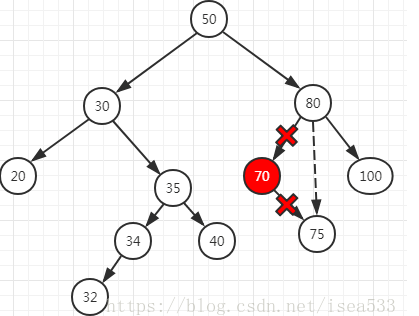
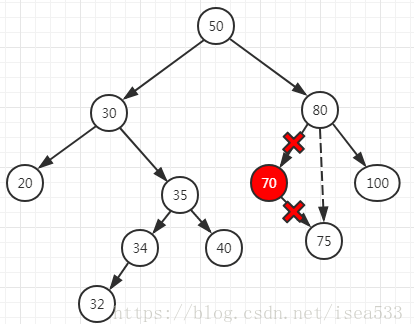
删除分为三种，直接删除叶子节点；只有一个孩子，与孩子交换后删除即可；有两个孩子，则需要找下一个比他大的数替换该数（中序遍历可以得到树的序列）

第一种:

第二种：

第三种：