上一章的二叉搜索树(平均时间复杂度O(n)),很容易在n个长度下形成高度为n-1的一条链,为了避免这种情况,引入红黑树,红黑树是许多“平衡”搜索树中的一种,可以保证在最坏情况下基本动态集合操作时间复杂度为O(lgn) 。
1.红黑树性质
红黑树是一棵二叉搜索树,它在每个结点上增加了一个存储位来表示结点的颜色,可以使RED或BLACK。通过对任何一条从根到叶子的简单路径上各个结点的颜色进行约束,红黑树确保没有一条路径会比其他路径长出2倍,因而是近似于平衡的。
树中每个结点包含5个属性:color、key、left、right。
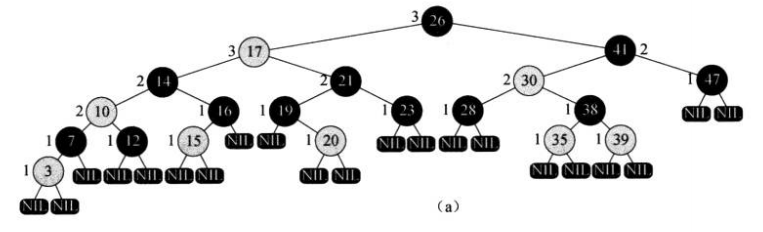
一棵红黑树需要满足以下条件:
- 每个结点是红色或者黑色的。
- 根节点是黑色的。
- 每个叶结点是黑色的。
- 如果一个结点是红色的,则它的两个子结点都是黑色的。
- 对每个结点,从该结点到所有后代叶结点的简单路径上,均包含数目相同的黑色结点。
从某个结点x出发(不含该结点),到达一个叶结点的任意一条简单路径上的黑色结点个数称为该结点的黑高,记为bh(x)。
一棵有n个内部结点的红黑树的高度至多为2lg(n+1)。即h<=2lg(n+1)。
而所有的搜索、求最大最小值、找前驱后置均可以在O(lgn)内完成。
可以使用一个黑色的哨兵代替所有的NIL结点,这样可以节省空间。
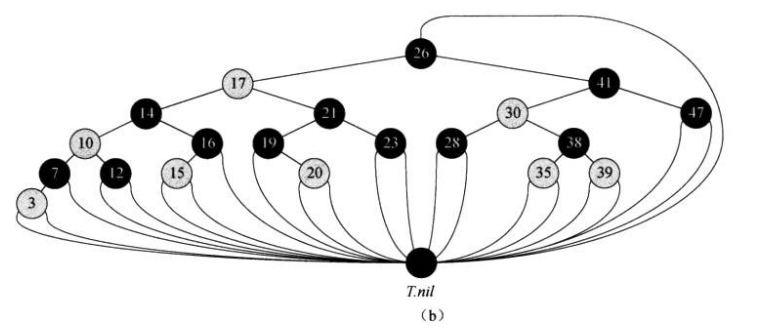
而一般,我们为了省略画图,画成这样:
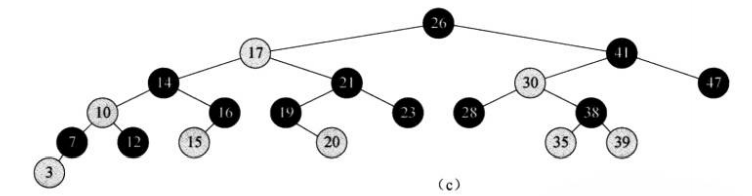
2.旋转
由于插入和删除可能会破坏红黑树平衡的性质,因此在插入和删除之后,可能需要通过旋转来继续满足红黑树的性质。
左右旋如下图所示:

左右旋函数:
def left_rotate(self, node, pre):
"""
左旋(node的左节点旋转到node当前位置
:param node:
:param pre:
:return:
"""
next = node.right
# 如果交换的点是父节点的左孩子
if pre.right == node:
pre.right = next
node.right = next.left
next.left = node
# 如果交换的点是父节点的右孩子
if pre.left == node:
pre.left = next
node.right = next.left
next.left = node
def right_rotate(self, node, pre):
"""
右旋(node的右节点旋转到node当前位置
:param node:
:param pre:
:return:
"""
next = node.right
# 如果交换的点是父节点的左孩子
if pre.right == node:
pre.right = next
node.left = next.right
next.right = node
# 如果交换的点是父节点的右孩子
if pre.left == node:
pre.left = next
node.left = next.right
next.right = node
如图,我们可以通过一个实例:先打印当前图的前序以及中序遍历来确定当前树:

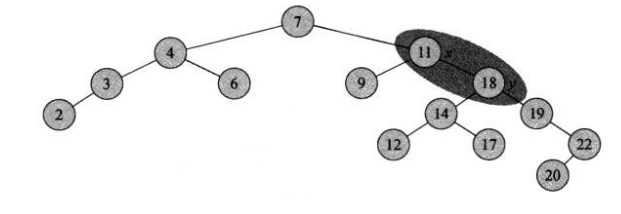
调用左旋之后再次输出当前树:

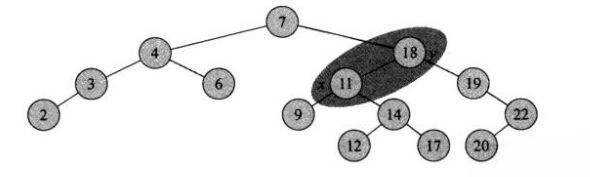
3.插入
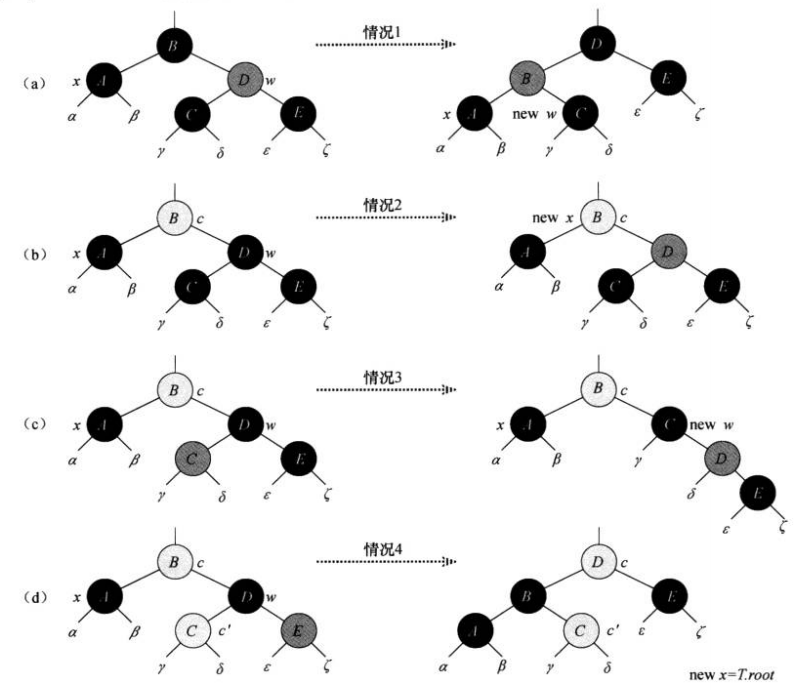
插入分几种情况,除了像二叉树一样插入,还要做一些操作保持红黑树性质。分以下四种情况:
第一种情况,如果插入的结点是根节点,则直接变成黑色。

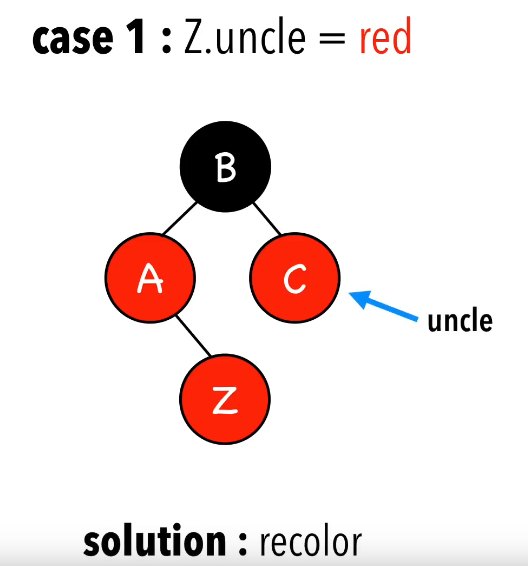
第二种情况是插入点的叔叔结点为红色,解决办法是重新染色:
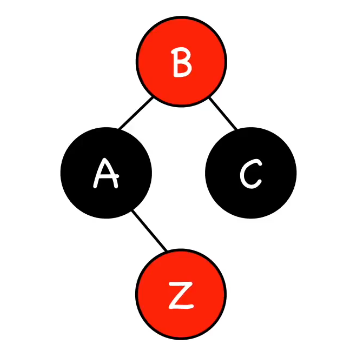
第三种情况是插入结点的叔叔是黑色(三角形),解决方法是旋转:
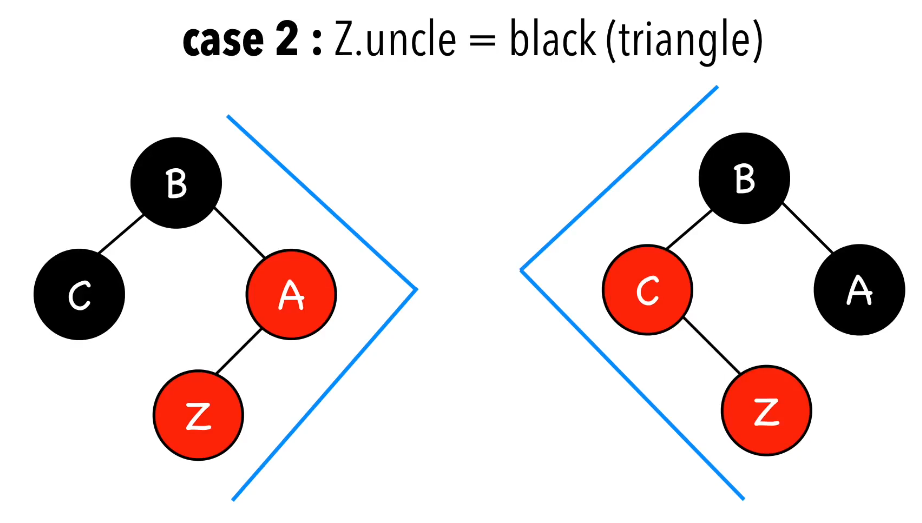
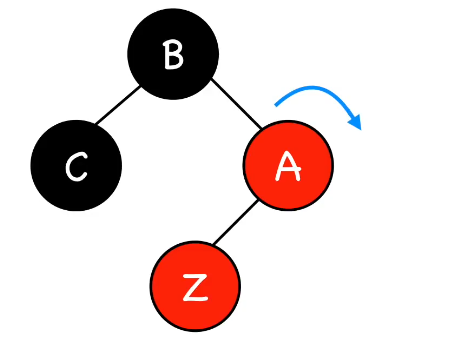
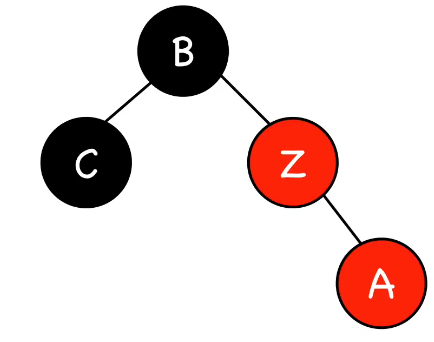
最后一种情况是插入结点的叔叔是黑色(线性),解决方法依然是旋转:
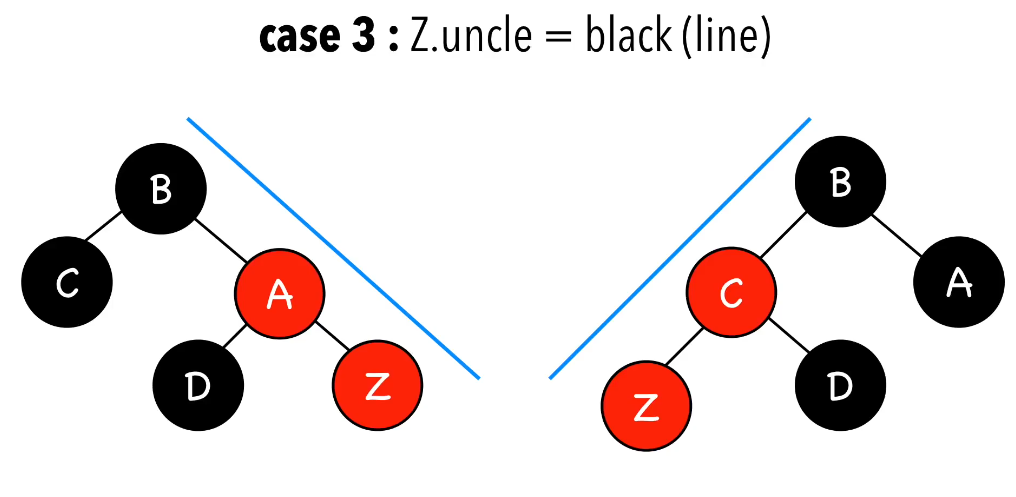
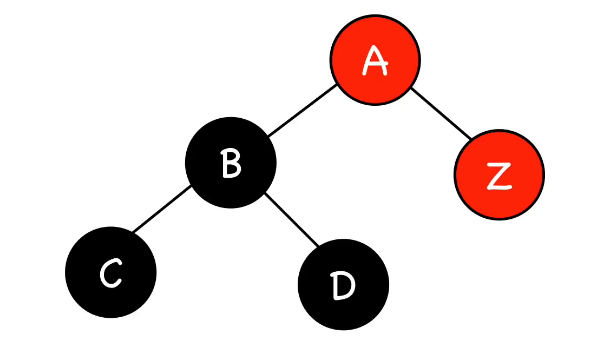
4.删除
删除结点的时间复杂度与插入一样,依然是O(lgn)。
有以下几种情况:
0 条评论