
动态规划(dynamic programming)与分值方法相似,都是通过组合子问题的解来求解原问题。
分治方法将问题划分为互不相交的子问题,递归地求解子问题,再将他们组合起来,求出原问题的解。
而动态规划应用于子问题重叠的情况,即不同的子问题具有公共的子子问题。通常用来求解最优化问题(optimization problem)。
我们通常按照如下4个步骤来设计一个动态规划算法:
- 刻画一个最优解的结构特性
- 递归地定义最优解的值
- 计算最优解的值,通常采用自底向上的方法。
- 利用计算出的信息构造一个最优解。
1.钢条切割
本例举了一个一维的动态规划栗子,如下,不同长度的钢条价钱不一样,现在求长度为n的钢条怎么切获利最多。

现在有两种思路:
1.假如现在又一个钢管,我们切割问题之后就变成了两个钢管的切割问题,我们通过两个相关子问题的最优解,并在所有可能的两段方案中找出最大值,构成原问题的最优解,我们称钢条切割问题满足最优子结构(optimal substructure)。
2.钢条切割还存在一种相似但是更为简单的递归求解法,我们将钢条从左边切割ixa一个长度为i的一段,对右边剩下的n-i长度进行递归求解(切割),对左边则不再进行切割。即现在的问题为左边的价格和右边切割得到的最优解,从寻找两个子问题最优解变成了一个。
那么我们先来实现一下第二种较简单的方法:
def CUT_OD(self, length, cost):
"""
钢管切割
:param length:钢管长度
:param cost:每个长度的价格(索引即长度)
:return:
"""
# 处理钢管长度为0的情况
if length == 0:
return 0
# 初始化结果(最优解)
q = -1
for i in range(1, length+1):
# 求解最优解
q = max(q, self.CUT_OD(length - i, cost) + cost[i])
return q

但是这种运行效率十分低,因为进行了过多的重复运算,当length上升时,运行时间指数级上升,下图是当长度为4时的调用树,运行时间为n的指数函数。
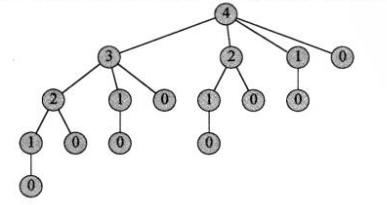
于是我们试图使用一个更高效率的动态规划算法来求解最优钢条切割问题:
第一种方法:既然我们把好多时间都用来做重复性的工作了,那我们使用一个数组(链表)来记录那些我们已经记录过的结果,这样不就快了么,我们称这个方法叫带备忘的自顶向下法(top-down with memoization)。
第二种方法:这种方法一般需要恰当定义子问题“规模”的概念,使得任何子问题的求解都只依赖于更小的子问题求解。因此我们可以将子问题按规模排序,按由小到大依次求解。我们称这种方法叫自底向上法(bottom-up method)。
但是两种算法的渐进时间相同。
下面是加入了备忘机制的动态规划算法:
def memoized_CUT_ROD(self, length, cost):
"""
钢管切割
:param length:钢管长度
:param cost:每个长度的价格(索引即长度)
:return:
"""
# 初始化切割价格数组,并直接定义长度0获益0(仅第一次初始化)
if self.value is None:
self.value = [-1 for _ in range(length + 1)]
self.value[0] = 0
# 如果计算过当前长度的最优解,直接返回
if self.value[length] >= 0:
print('return', length)
return self.value[length]
print('compute', length)
for i in range(1, length + 1):
self.value[length] = max(self.value[length], self.memoized_CUT_ROD(length - i, cost) + cost[i])
return self.value[length]

自底向上的版本:
def bottom_up_CUT_ROD(self, length, cost):
"""
自底向上
:param length:
:param cost:
:return:
"""
# 初始化切割价格数组,并直接定义长度0获益0(仅第一次初始化)
if self.value is None:
self.value = [-1 for _ in range(length + 1)]
self.value[0] = 0
for i in range(1, length + 1):
for j in range(1, i + 1):
self.value[length] = max(self.value[length], self.bottom_up_CUT_ROD(i - j, cost) + cost[j])
return self.value[length]
两种求解方法复杂度均为O(n^2)。
2.矩阵链乘法
举例二维动态规划:利用矩阵的乘法结合律寻找矩阵相乘中计算次数最少的相乘组合。
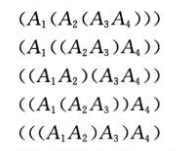
步骤一:最优括号化方案的结构特征
动态规划的第一步就是寻找最优子结构,然后利用这种子结构问题的最优解构造出原问题的最优解。
本例中的结构特征就是,假设我们在A_{1~j}以A_k为分割点,那么A_{1~k}和A_{k+1~j}分别使用最优分割代价来计算 A_{1~j} 的最小代价。
步骤二:一个递归求解方案
我们定义一个矩阵,对于m[i,j]的定义如下:矩阵A_{ i,j }所需标量乘法次数的最小值。
那么对于在 A_k 分割的矩阵序列 A_{i~j} ,我们有:
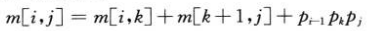
其中p为两个矩阵的行列参数,因此:
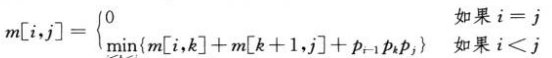
步骤三:计算最优代价
即使用代码计算最优解:
def matrix_chain_order(self, p):
"""
:param p:
:return:
"""
if self.value is None:
self.value = [[float('inf') for _ in range(len(p))] for _ in range(len(p))]
self.cut_loc = [[-1 for _ in range(len(p))] for _ in range(len(p))]
p_length = len(p)
# 初始化对角线元素
for i in range(p_length):
self.value[i][i] = 0
# 长度为n的 (先计算两两的括号的、三三括号的。。。)
for l in range(2, p_length + 1):
# 寻找length-n+1 个长度为n的排序
for i in range(0, p_length - l + 1):
j = i + l - 1
for k in range(i, j):
if self.value[i][j] > self.value[i][k] + self.value[k + 1][j] + p[i][0] * p[k][1] * p[j][1]:
self.value[i][j] = self.value[i][k] + self.value[k + 1][j] + p[i][0] * p[k][1] * p[j][1]
self.cut_loc[i][j] = k
输入为数组p = [[30, 35], [35, 15], [15, 5], [5, 10], [10, 20], [20, 25]],代表矩阵0为30*35,矩阵1为35*15……
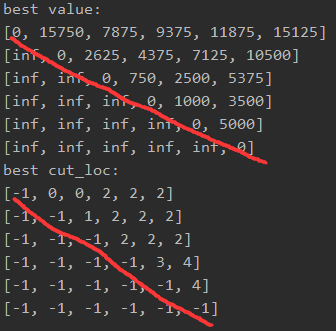
可以看出,当我们试图知道A_{0~5}的最优解时,需要做15125([0][5])次乘法,而需要在idx2处分割,即。 A_{0~2}和 A_{3~5},而 A_{0~2}图中为0,则继续分为 A_{0}和 A_{1~2} ; A_{3~5}为4,即又分割为 A_{4~5} 和 A_{6}以此计算出最优
((A_0(A_1*A_2))((A_4*A_5)A_6)))。
步骤四:构造最优解
输出结果:
def print_optimal_parens(self, i, j):
"""
打印括号分布
:param i: from
:param j: to
:return:
"""
if i == j:
print('A_', i, ' ', end='')
else:
print('(', end='')
self.print_optimal_parens(i, self.cut_loc[i][j])
self.print_optimal_parens(self.cut_loc[i][j] + 1, j)
print(')', end='')
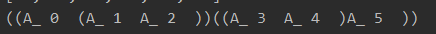
3.动态规划原理
1.最优子结构
动态规划的思想就是找到最优子结构,但是同时需要注意,并不是所有的问题都具有最优子结构比如下图:
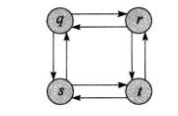
如果我们找最短距离,我们可以找到单步最优子结构,但是如果我们是找最长距离,那么我们永远也找不到最优子结构(因为永远会有更长的)。
2.重叠子问题
适用于动态规划方法求解的最优化问题应该具备的第二个性质是子问题空间必须足够小,并且有反复求解的相同子问题(如前面钢条问题对于同一区间利润的反复求解),我们就称这个最优化问题具有重叠子问题。
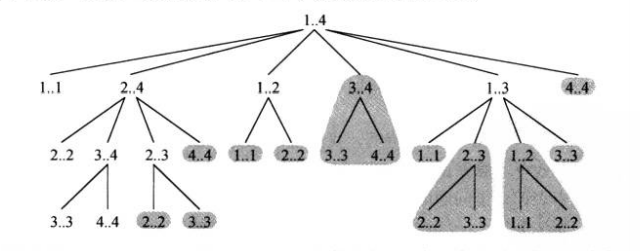
如上图,在钢条利益计算时,重复计算了多组相同解,如果使用动归记录这些值就不需要进行重复计算,从而减少运行时间。
3.重构最优解
不仅记录局部最优结果,还要记录局部最优解,以降低下一步需要计算出全局最优解时的代价。
4.最长公共子序列
实际上就是KMP算法。在这里不做说明,上一个视频。
5.最优二叉搜索树
假如我们需要进行一个树查找操作,如果要快速的进行查找操作,可以使用平衡二叉树或者红黑树来进行,但是假如其中某个节点需要频繁的进行查询操作,而恰好这个结点又是树的叶子结点,那么无疑也是需要很长的时间来进行查找操作。
解决这一问题的办法就是最优二叉搜索树。我们将查询次数较多的点向根靠拢,将查询次数不那么多的点向叶子靠拢。
比如如下的例子,其中,p表示该数字出现的概率,q表示不是该数字(是该区间)出现的概率,也就是p_i+q_i=1:

对于这个平衡二叉树,期望搜索代价为2.80。
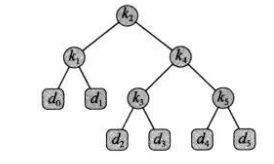
而对于下面这个(最优)二叉搜索树,期望搜索代价只有2.75。
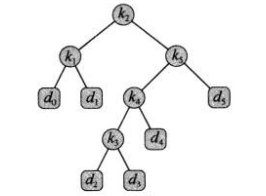
在生成这样一个最优二叉搜索树时也是遵循动态规划的思想,即每一个子树都是当前的最优解,我们从叶子节点选取一个概率最低的两个点作为根,然后逐步向上求和取最低,最终构造出一个最优二叉搜索树。
0 条评论