【算法导论】贪心算法

求解最优化问题的算法通常需要经过一系列的步骤，在每个步骤都面临多种选择。对于许多最优化问题，使用动态规划算法来求解最优解问题有些杀鸡用牛刀了，可以使用更简单、更高效的算法，也就是贪心算法来解决这一问题。

需要主义，贪心算法并不保证得到的是最优解，但是对于很多问题确实可以得到最优解。

1.活动选择问题

第一个例子是调度竞争共享资源的问题，目标是选出一个最大的互相兼容的活动集合。

假设有几个n个长度的集合S，这些活动占用一个共同的资源，包括一个开始时间和结束时间，我们需要选取一个能够接纳最多活动的序列集合。

1.动态规划解决活动选择问题

对于使用动态规划解决这类问题，显而易见的 最优子结构是i~j时间内的最优解。

代码如下：

def choose_best_activity_with_dp(self, S, i, j):
    """
    使用动态规划计算最佳活动选择
    :param S: 活动列表
    :param i: 起始时间
    :param j: 终止时间
    :return:
    """
    # 用来保存需要在哪个点分割
    value = [0 for _ in range(j - i + 1)]
    # 用来保存从i到j最多有几个活动
    count = [[0 for _ in range(j - i + 1)] for _ in range(j - i + 1)]
    # 初始化，每个活动的起始终止时间置为1
    for each in S:
        count[each[1]][each[2]] = 1
    # dp
    for x in range(1, len(value)):
        for y in range(x):  # 这个相当于上面说的k
            if count[i][y] + count[y][x] > count[i][x]:
                count[i][x] = count[i][y] + count[y][x]
                value[x] = y
    return value

2.贪心选择解决活动选择问题

如果我们让每一选择活动之后剩余资源越多，那么我们可选择的是不是也就越多呢，这就是贪心思想，对于这道题，我们每一步都选择剩余时间最多的，那么我们就可以选择到最多的活动。

代码如下：

def greedy_choose(self, S, i, j):
    """
    贪心算法解决活动问题
    :param S:
    :param i:
    :param j:
    :return:
    """
    # 返回点集合
    return_list = []

    def choose_one(i):
        """
        选择一个i时间点之后开始，并且持续时间最短的活动
        :param i:
        :return:
        """
        min_end_time = float('inf')
        return_one = None
        for each in S:
            if each[1] >= i and each[2] < min_end_time:
                min_end_time = each[2]
                return_one = each
        return return_one

    x = i
    while x <= j:
        one = choose_one(x)
        if one is None:
            return return_list
        return_list.append(one)
        x = one[2]

2.贪心算法原理

1.贪心选择性质

第一个关键要素是贪心选择性质，我们可以通过做出局部最优（贪心）选择来构造出全局最优解。也就是说，在每一步我们都考虑最优选择，而不必考虑子问题的解。

在动归中，我们每一步都要进行一次选择，但是选择通常依赖于子问题的解。

在贪心中，我们总是做出当时看最佳的选择，然后求解剩下的唯一的子问题。

总结来说就是，动归要求解出每一种可能之后才做出选择，而贪心早早的就选择好了，再计算下一步。

2.贪心对动态规划

由于贪心和动态规划都利用了最优子结构性质，而两种方法有一点细微差别，我们研究一个经典的最优化问题的两个变形。

0-1背包问题：一个小偷正在抢劫商店，发现了n件商品，第i个商品价值v_i元，重w_i磅。这个小偷希望拿走价值尽量高的商品，但是他的背包最多能容纳W磅重的商品。他应该拿哪些东西呢？

分数背包问题：和0-1背包类似，不同的是，这里小偷可以选择拿走一部分，而不是0-1背包中的二元选择问题。

可以理解成0-1背包是金锭，分数背包是金砂。

对于分数背包问题，我们可以使用贪心算法，计算v_i/w_i，按照从高到低拿物品即可。

而对于0-1背包问题，我们就不可以这么做，因为这么拿往往可能会让背包产生空闲，从而降低整体的价值。

0-1背包代码：

def shop_with_dp(self, value, bag_size):
    """
    0-1背包
    :param value:
    :param bag_size:
    :return:
    """
    result = [[0 for _ in range(bag_size+1)] for _ in range(len(value[0]))]

    for i in range(0, len(value[0])):
        for j in range(0, bag_size+1):
            if value[i][1] <= j:
                if result[i][j] < result[i-1][j - value[i][1]] + value[i][2]:
                    result[i][j] = result[i-1][j - value[i][1]] + value[i][2]
            else:
                result[i][j] = result[i - 1][j]
    return result[-1][-1]

分数背包代码：

def shop_with_greedy_algorithm(self, value, bag_size):
    """
    分数背包问题
    :param value:
    :param bag_size:
    :return:
    """
    each_value = [0 for _ in range(len(value))]
    total_value = 0
    # 计算商品均价
    for i in range(len(each_value)):
        each_value[i] = value[i][2] / value[i][1]
    # 循环装满背包
    while bag_size > 0:
        most_valued_idx = each_value.index(max(each_value))
        if value[most_valued_idx][1] < bag_size:
            # 对应背包能装满商品的情况
            bag_size -= value[most_valued_idx][1]
            total_value += each_value[most_valued_idx] * value[most_valued_idx][1]
            each_value.remove(each_value[most_valued_idx])
            value.remove(value[most_valued_idx])
        else:
            # 对应背包不能装全部商品的情况
            total_value += bag_size * each_value[most_valued_idx]
            bag_size = 0
        pass
    return total_value

3.哈夫曼编码

哈夫曼编码可以很有效地压缩数据，通常可以可以节约20~90%空间。

我们将待压缩数据看做字符系列，根据每个字符序列，贪心的构造出字符的最优二进制表示。

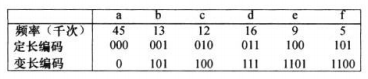
定长编码只是根据字符出现的频率对字符进行二进制编号。

而变长编码，画出如下哈弗曼树

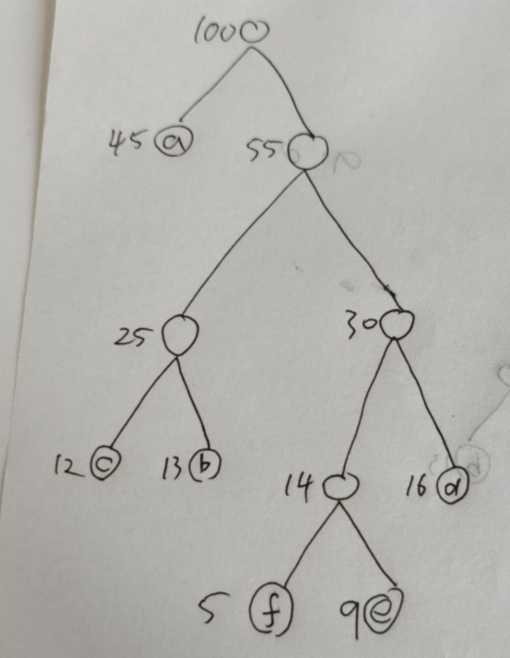
然后左叶子定义为0，右叶子定义为1，即可找出变长编码。

构造哈夫曼编码代码（只写到生成哈夫曼树）：

def huffman_code(self, data):
    """
    生成哈夫曼编码
    :param data:
    :return:
    """
    huffman_tree = self.build_huffman_tree(data)
    pass

def build_huffman_tree(self, data):
    """
    构造哈弗曼树
    :param data:
    :return:
    """
    huffman_str = []
    huffman_tree = []

    def find_min():
        """
        寻找最小的两个点
        :return:
        """
        if len(data) == 1:
            return data[0], None
        min_data = float('inf')
        # 最小点
        most_min = data[0]
        # 次小点
        secd_min = data[0]
        # 遍历寻找最小点
        for each in data:
            if each[1] < min_data:
                most_min = each
                min_data = each[1]
        data.remove(most_min)
        min_data = float('inf')
        # 遍历寻找最小点
        for each in data:
            if each[1] < min_data:
                secd_min = each
                min_data = each[1]
        data.remove(secd_min)
        # 将这两个点的根加回去
        data.append(['*', most_min[1] + secd_min[1]])

        return most_min, secd_min

    def connect_tree():
        """
        连接树
        :return:
        """
        # 最小点
        most_min = huffman_str[-1]
        # 次小点
        secd_min = huffman_str[-2]

        flag = most_min[1] + secd_min[1]
        root_idx = 0
        # 遍历寻找最小两个点的根
        for i in range(len(huffman_str) - 1, -1, -1):
            if huffman_str[i][1] == flag:
                root_idx = i
                break
            pass
        # 连接左右子树
        huffman_tree[root_idx].left = huffman_tree[-1]
        huffman_tree[root_idx].right = huffman_tree[-2]
        # 移除这两个点
        huffman_str.remove(most_min)
        huffman_str.remove(secd_min)
        huffman_tree.remove(huffman_tree[-1])
        huffman_tree.remove(huffman_tree[-1])
        pass

    # 构造哈夫曼字符串（因为没办法连成树，先计算哈夫曼树的列表表示）
    for i in range(len(data)):
        most_min, secd_min = find_min()
        if secd_min is None:
            huffman_str.insert(0, most_min)
            continue
        huffman_str.insert(0, most_min)
        huffman_str.insert(0, secd_min)
        pass
    # 利用已知的哈夫曼顺序构造哈弗曼树
    for each in huffman_str:
        huffman_tree.append(tree(each[1], None, None, None))
    for i in range(int(len(huffman_str) / 2)):
        connect_tree()