【算法导论】基本的图算法

1.图的表示

对于图G=(V,E)，我们可以用两种标准方法表示。一种是邻接链表，一种是邻接矩阵。

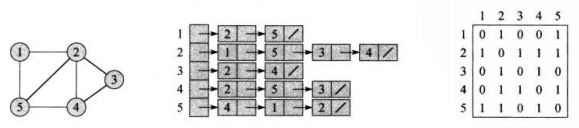
如下图分别就是图，图的邻接链表表示，图的邻接矩阵表示。

对于稠密图，我们一般使用邻接矩阵来表示，对于稀疏图，我们一般使用邻接链表来表示。

2.广度优先搜索

广度优先搜索是最简单的图搜索算法之一，也是许多图算法的原型。

广度优先遍历顾名思义就是尽可能广的遍历，先遍历当前节点的所有孩子节点，再向下遍历直到遍历完全整个树。

def bfs(self, graph, init_idx, flag=None):
    """
    广度优先遍历
    :param graph:
    :return:
    """
    result = []
    # 第一次运行的数据初始化
    if flag is None:
        flag = [0 for _ in range(len(graph))]
        flag[init_idx - 1] = 1
        result = [init_idx]
    temp_list = []
    for j in range(len(flag)):
        if graph[init_idx - 1][j] == 1 and flag[j] == 0:
            result.append(j + 1)
            temp_list.append(j)
            flag[j] = 1
    # 递归广搜
    for i in range(len(temp_list)):
        result.extend(self.bfs(graph, temp_list[i] + 1, flag))
    return result

最短路径

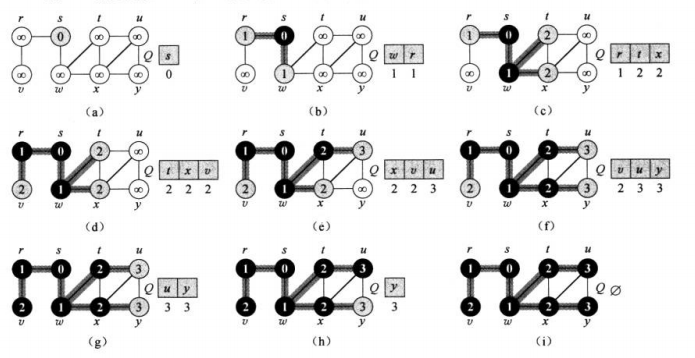
广度优先遍历也可以用来找最短距离，因为是层级遍历，如果从根遍历，到目标节点经过几层，则最短路就为多少。

3.深度优先搜索

深度优先遍历是从图的一条边入手，一直向下直至没办法再遍历为止。

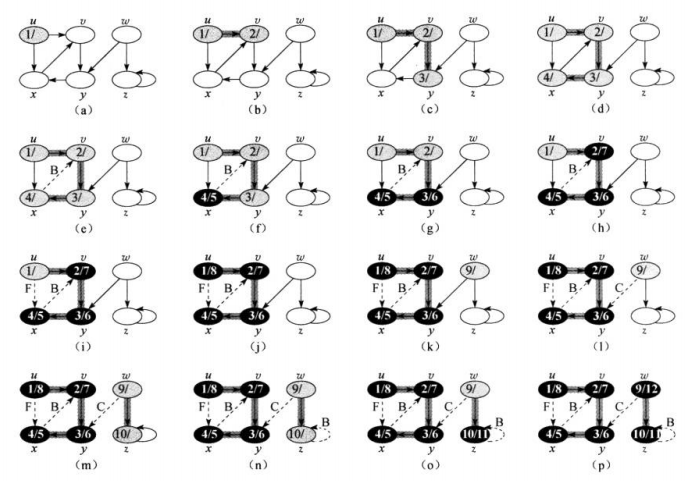
代码：

def dfs(self, graph, init_idx, flag=None):
    """
    深度优先遍历
    :param graph:
    :param init_idx:
    :param flag:
    :return:
    """
    result = [init_idx]
    if flag is None:
        flag = [0 for _ in range(len(graph))]
    for i in range(len(graph)):
        if graph[init_idx - 1][i] == 1 and flag[i] == 0:
            flag[i] = 1
            result.extend(self.dfs(graph, i + 1, flag))
    return result

4.拓扑排序

对于一个有向无环图来说，其拓扑排序是G中所有节点的一种线性次序。

举个例子，如果是一些待完成事项，那么拓扑排序就是一个你完成该事项的顺序。

比如如下学习路线：

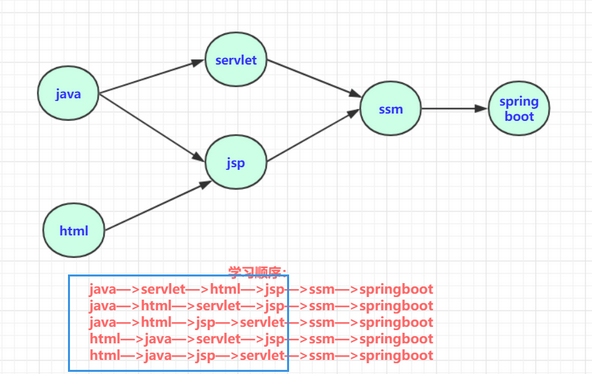
我们可以整理出5种学习路线，而这五条路线就是上图的拓扑排序。

那么怎么得到拓扑排序呢？

找到一个入度为0的点（java和html），然后去掉它的出度，继续寻找入度为0的点。直至没有点（如果还有点则证明此图中有环）